Duoprisma

Conjunto de ( $p-q$ )-duoprismas uniformes
Tipo	4-politopos uniformes prismáticos
Símbolo de Schläfli	${p}\times{q}$
Diagrama de Coxeter-Dynkin
Celdas	Prismas $p q$ -gonales, prismas $q p$ -gonales
Facetas	$pq$ Cuadrados, $p q$ -gonos, $q p$ -gonos
Aristas	$2 pq$
Vértices	$pq$
Figura de vértice	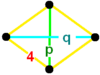Disfenoide
Simetría	$[p,2, q]$ , orden $4 pq$
Dual	$p-q$ duopirámide
Propiedades	Convexo, isogonal

Conjunto de ( $p-p$ )-duoprismas uniformes
Tipo	4-politopo uniforme prismático
Símbolo de Schläfli	${p}\times{p}$
Diagrama de Coxeter-Dynkin
Celdas	Prismas $2 p p$ -gonales
Facetas	$p 2$ Cuadrados, $2 p p$ -gonos
Aristas	$2 p 2$
Vértices	$p 2$
Simetría	$[p,2, p]= [2 p,2 +$ ,2p],}} orden $8 p 2$
Dual	$p-p$ duopirámide
Propiedades	Convexo, isogonal, isoedral

En geometría de 4 o más dimensiones, un duoprisma^[1] (o también doble prisma) es un politopo resultante del producto cartesiano de dos politopos, cada uno de dos dimensiones o más. El producto cartesiano de un $n$ -politopo y de un $m$ -politopo es otro $(n + m)$ -politopo, donde $n$ y $m$ son de dimensión 2 (polígonos) o superior.

Dada su definición, los duoprismas de menor dimensión posible están definidos en el espacio tetradimensional como polícoros generados mediante el producto cartesiano de dos polígonos definidos en el espacio euclídeo bidimensional. Más precisamente, es el conjunto de puntos:

P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}

donde $P 1$ y $P 2$ son los conjuntos de puntos contenidos en los respectivos polígonos. Tal duoprisma es convexo si ambas bases son convexas, y está acotado por celdas prismáticas.

Nomenclatura

Los duoprismas de cuatro dimensiones se consideran 4 politopos prismáticos. Un duoprisma construido a partir de dos polígonos regulares de la misma longitud de arista es un duoprisma uniforme.

Un duoprisma formado por n-polígonos y por m-polígonos se nombra anteponiendo duoprisma a los nombres de los polígonos base, por ejemplo: un duoprisma triangular-pentagonal es el producto cartesiano de un triángulo y de un pentágono.

Una forma alternativa y más concisa de especificar un duoprisma particular es anteponiendo números que denoten los polígonos base, por ejemplo: 3,5-duoprisma para el duoprisma triangular-pentagonal.

Otros nombres alternativos:

Prisma q-gonal-p-gonal
Duoprisma q-gonal-p-gonal
Hiperprisma q-gonal-p-gonal

El término duoprisma fue acuñado por George Olshevsky, a partir de la expresión doble prisma. John Horton Conway propuso un nombre similar, proprisma, para denominar a un prisma producto, el producto cartesiano de dos o más politopos de dimensión al menos dos. Los duoprismas son proprismas formados a partir de exactamente dos politopos.

Ejemplo de un 16-16 duoprisma

Diagrama de Schlegel Se muestra la proyección desde el centro de un prisma 16-gonal y todos menos uno de los prismas 16-gonales opuestos.	Desarrollo Se muestran los dos conjuntos de prismas 16-gonales. Las caras superior e inferior del cilindro vertical están conectadas cuando se pliegan juntas en 4D

Geometría de duoprismas de 4 dimensiones

Un duoprisma uniforme de 4 dimensiones se crea mediante el producto de un polígono regular de n lados y de un polígono regular de m lados con la misma longitud de arista. Está delimitado por n prismas m-gonales; y por m prismas n-gonales. Por ejemplo, el producto cartesiano de un triángulo y un hexágono es un duoprisma acotado por 6 prismas triangulares y 3 prismas hexagonales.

Cuando m y n son idénticos, el duoprisma resultante está limitado por 2n prismas n-gonales idénticos. Por ejemplo, el producto cartesiano de dos triángulos es un duoprisma acotado por 6 prismas triangulares.
Cuando m y n son iguales a 4, el duoprisma resultante está limitado por 8 prismas cuadrados (cubos) y es idéntico al teseracto.

Los prismas m-gonales están unidos entre sí a través de sus caras m-gonales y forman un bucle cerrado. De manera similar, los prismas n-gonales están unidos entre sí a través de sus caras n-gonales y forman un segundo bucle perpendicular al primero. Estos dos bucles están unidos entre sí a través de sus caras cuadradas y son mutuamente perpendiculares.

A medida que m y n se acercan al infinito, los duoprismas correspondientes se acercan al duocilindro. Como tal, los duoprismas son útiles como aproximaciones no cuádricas drl duocilindro.

Desarrollos 3D

3-3
3-4	4-4
3-5	4-5	5-5
3-6	4-6	5-6	6-6
3-7	4-7	5-7	6-7	7-7
3-8	4-8	5-8	6-8	7-8	8-8
3-9	4-9	5-9	6-9	7-9	8-9	9-9
3-10	4-10	5-10	6-10	7-10	8-10	9-10	10-10

Proyecciones en perspectiva

Una proyección en perspectiva centrada en una celda hace que un duoprisma parezca un toro, con dos conjuntos de celdas ortogonales (prismas p-gonales y q-gonales).

Diagramas de Schlegel
6-prisma	6-6 duoprisma

Un prisma hexagonal, proyectado en el plano en perspectiva, centrado en una cara hexagonal, parece un hexágono doble conectado por cuadrados (distorsionados). De manera similar, un duoprisma 6-6 proyectado en 3D se aproxima a un toro, hexagonal tanto en planta como en sección.

Los duoprismas p-q son idénticos a los duoprismas q-p, pero se ven diferentes en estas proyecciones porque se proyectan en el centro de diferentes celdas.

Diagramas de Schlegel
3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Proyecciones ortogonales

Las proyecciones ortogonales centradas en el vértice de los duoprismas p-p muestran simetría [2n] para grados impares y [n] para grados pares. Hay n vértices proyectados hacia el centro. Para el par de valores 4,4, representa el plano de Coxeter A₃ del teseracto. La proyección 5,5 es idéntica al triacontaedro rómbico en 3D.

Proyección ortogonal de p-p duoprismas en vista alámbrica
Impares
3-3		5-5		7-7		9-9

[3]	[6]	[5]	[10]	[7]	[14]	[9]	[18]
Pares
4-4 (teseracto)		6-6		8-8		10-10

[4]	[8]	[6]	[12]	[8]	[16]	[10]	[20]

Politopos relacionados

Proyección estereográfica de un duocilindro en rotación, una superficie dividida en los cuadrados del poliedro oblicuo {4,4|n} (representados con el patrón de un tablero de ajedrez)

El poliedro oblicuo regular {4,4|n} existe en el 4 espacio como las n² caras cuadradas de un n-n duoprisma, incluyendo todas las 2n² aristas y los n² vértices. Las 2n caras n-gonales han sido eliminadas (los poliedros oblicuos se pueden ver de la misma manera mediante un duoprisma n-m, pero no son regulares).

Duoantiprisma

Figura de vértice de un p-q duoantiprisma, un girobifastigium

Proyección estereográfica de un gran duoantiprisma, centrada en uno de sus antiprismas cruzados pentagrámicos

Al igual que los antiprismas considerados como prismas alternados, existe un conjunto de duoantiprismas de 4 dimensiones: polícoros que puede crearse mediante una operación alternación aplicada a un duoprisma. Los vértices alternados crean células tetraédricas no regulares, excepto en un caso especial, el duoprisma 4-4 (teseracto), que crea el hexadecacoron uniforme (y regular). El de 16 celdas es el único duoantiprisma uniforme convexo.

Los duoprismas , t_0,1,2,3{p,2,q}, se pueden alternar en , ht_0,1,2,3{p,2,q}, los duoantiprismas, que no pueden uniformarse en general. La única solución uniforme convexa es el caso trivial de p=q=2, una construcción de simetría inferior del teseracto , t_0,1,2,3{2,2,2}, con su alternancia generando el hexadecacoron, , s{2}s {2}.

La única solución uniforme no convexa es p=5, q=5/3, ht_0,1,2,3{5,2,5/3}, , construida a partir de 10 antiprismas pentagonales, 10 antiprismas cruzados pentagramáticos y 50 tetraedros, polícoro conocido como gran duoantiprisma (gudap).^[2]^[3]

Ditetragoltriatos

También están relacionados los ditetragoltriatos u octagoltriatos, formados llevando el octógono (considerado un ditetragón o un cuadrado truncado) a un p-gono. El octógono de un p-gono se puede definir claramente si se supone que el octógono es el recubrimiento convexo de dos rectángulos perpendiculares; entonces el ditetragoltriato p-gonal es el recubrimiento convexo de dos duoprismas p-p (donde los p-gonos son similares pero no congruentes y tienen diferentes tamaños) en orientaciones perpendiculares. El polícoro resultante es isogonal y tiene 2p prismas p-gonales y p² trapezoprismas rectangulares (un cubo con simetría D_2d), pero no es uniforme. La figura del vértice es una bipirámide triangular.

Duoantiprismoides

Al igual que los duoantiprismas como duoprismas alternados, hay un conjunto de duoantiprismoides p-gonales creados alternando los ditetragoltriatos 2p-gonales, generando antiprismas p-gonales y tetraedros mientras se reinterpretan los espacios bipiramidales triangulares no coreálmicos como dos tetraedros. La figura resultante generalmente no es uniforme excepto en dos casos: el gran antiprisma y su conjugado, el duoantiprismoide pentagrámico (con p = 5 y 5/3 respectivamente), representado como la alternancia de un ditetragoltriato decagonal o decagrámico. La figura de vértice es una variante de la esfenocorona.

k_22 politopos

El 3-3 duoprisma, -1₂₂, es el primero de una serie dimensional de politopos uniformes, expresados por Harold Scott MacDonald Coxeter como la serie k₂₂. El duoprisma 3-3 es la figura de vértice del segundo politopo, el 5-símplex birrectificado. La cuarta figura es un panal euclídeo, el 2₂₂, y el último es un panal hiperbólico paracompacto, 3₂₂, con el grupo de Coxeter [3^2,2,3], Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wiki.x.io/v1/»:): {\displaystyle {\bar{T}}_7} . Cada politopo uniforme se construye progresivamente a partir del anterior como su figura de vértice.

k₂₂ figuras en n dimensiones
Espacio	Finito			Euclídeo	Hiperbólico
n	4	5	6	7	8
Grupo de Coxeter	A₂A₂	E₆	${\tilde {E}}_{6}$ =E₆⁺	${\bar {T}}_{7}$ =E₆⁺⁺
Diagrama de Coxeter
Simetría	[[ 3^2,2,-1]]	[[ 3^2,2,0]]	[[ 3^2,2,1]]	[[ 3^2,2,2]]	[[ 3^2,2,3]]
Orden	72	1440	103,680	∞
Grafo				∞	∞
Nombre	−1₂₂	0₂₂	1₂₂	2₂₂	3₂₂

Véase también

Referencias

↑ The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook
↑ Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap
↑ http://www.polychora.com/12GudapsMovie.gif Archivado el 22 de febrero de 2014 en Wayback Machine. Animation of cross sections

Bibliografía

Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
Harold Scott MacDonald Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Datos: Q921050

[1] The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook

[2] Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap

[3] ttp://www.polychora.com/12GudapsMovie.gif Archivado el 22 de febrero de 2014 en Wayback Machine. Animation of cross sections

[1]

[2]

[3]

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8