Horóptera

Una horóptera es una curva espacial dada por el conjunto de puntos que proyectan en puntos con idénticas coordenadas en dos cámaras con iguales parámetros intrínsecos. La horóptera es, en general, una cúbica alabeada y es la intersección de un paraboloide hiperbólico y un cilindro.

Horóptera.

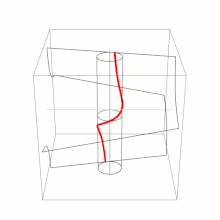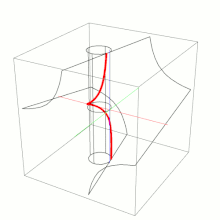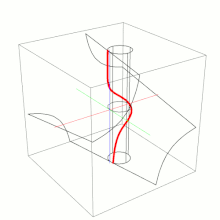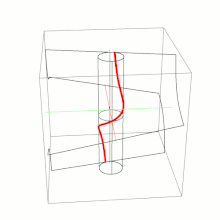
Su ecuación paramétrica es​

$x={\frac {2r}{1+\lambda ^{2}t^{2}}}$

$y={\frac {2r\lambda t}{1+\lambda ^{2}t^{2}}}$

$z=t$

donde $r$ es el radio del cilindro y $\lambda$ una constante.

En el estudio de la visión binocular, la horóptera es un volumen centrado en el punto de fijación que contiene todos los puntos del espacio que resultan en una única visión. Este volumen se puede identificar teóricamente como los puntos del espacio que corresponden en una imagen en ambas retinas, es decir, en puntos anatómicamente idénticos. Habitualmente se define de forma empírica utilizando algún criterio.

Historia del término

Según Glanville (1933), el término horóptera. fue introducido por François d'Aguilon (Franciscus aguilonius) en el segundo de sus seis libros sobre óptica en 1613. En 1818, G. U. A. Vieth argumentó a partir de bases geométricas que la horóptera debería ser un círculo que va a través del centro de fijación y los centros de las lentes de ambos ojos. Unos años después, J. Müller extrajo similares conclusiones a partir del plano horizontal que contiene el punto de fijación, aunque esperaba que la horóptera fuera una superficie en el espacio. La horóptera teórico-geométrica en el plano horizontal se acabó conociendo como "círculo de Vieth-Müller". En 1838, Charles Wheatstone inventó el estereoscopio, lo que permitió explorar la horóptera empírica.​ Encontró que existían muchos puntos del espacio que proporcionaban una visión única. Esto está muy apartado de la horóptera teórica.

Referencias

• Datos: Q1262259