Trapecio tangencial
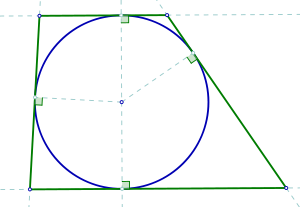
En la geometría euclídea, un trapecio tangencial, también llamado trapecio circunscrito, es un trapecio cuyos cuatro lados son tangentes a una circunferencia situada dentro del propio trapecio (su circunferencia inscrita o incírculo). Es un caso especial de un cuadrilátero tangencial, en el que al menos un par de lados opuestos son paralelos. Como en otros trapecios, los lados paralelos se llaman bases. Las aristas laterales pueden ser iguales (véase el trapecio tangencial isósceles a continuación), pero no tienen por qué serlo.
Casos especiales
editarCasos especiales de trapecios tangenciales son los rombos y los cuadrados.
Caracterización
editarSi el incírculo es tangente a los lados AB y CD en W e Y respectivamente, entonces un cuadrilátero tangencial ABCD también es un trapecio con lados paralelos AB y CD si y solo si:[1] : Thm. 2
y AD y BC son los lados paralelos de un trapecio si y solo si
Área
editarLa fórmula para el área de un trapecio se puede simplificar usando el teorema de Pitot para obtener una fórmula para el área de un trapecio tangencial. Si las bases tienen longitudes a y b, y cualquiera de los otros dos lados tiene una longitud c, entonces el área K viene dada por la fórmula[2]
El área se puede expresar en términos de las longitudes tangentes e, f, g, y h como[3] : p.129
![{\displaystyle K={\sqrt[{4}]{efgh}}(e+f+g+h).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef723678f235a25b2488c717837a47cb493f9bd)
Inradio
editarUsando la misma notación que para el área, el radio del incírculo es[2]
Su diámetro es igual a la altura del trapecio tangencial.
El inradio también se puede expresar en términos de longitudes tangentes como[3] : p.129
![{\displaystyle r={\sqrt[{4}]{efgh}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5760badfbf69d199976db4357edf238b525b132d)
Además, si las longitudes tangentes e, f, g y h dependen respectivamente de los vértices A, B, C, y D; y AB es paralelo a DC, entonces[1]
Propiedades del incentro
editarSi el círculo es tangente a las bases en P y Q, entonces P, I y Q son colineales, siendo I el incentro.[4]
Los ángulos AID y BIC en un trapecio tangencial ABCD, con bases AB y DC, son ángulos rectos.[4]
El incentro se encuentra en la mediana (también llamada segmento medio; es decir, el segmento que conecta los puntos medios de las aristas laterales).[4]
Otras propiedades
editarLa mediana (segmento medio) de un trapecio tangencial es igual a un cuarto del perímetro del trapecio. También es igual a la mitad de la suma de las bases, como en todos los trapecios.
Si se dibujan dos círculos, cada uno con un diámetro que coincide con las aristas laterales de un trapecio tangencial, entonces estos dos círculos son tangentes entre sí.[5]
Trapecio tangencial recto
editar
Un trapecio tangencial recto posee dos ángulos adyacentes rectos. Si las bases tienen longitudes a y b, entonces el radio es[6]
Así, el diámetro del incírculo es la media armónica de las bases.
El trapecio tangencial recto tiene el área[6]
Trapecio tangencial isósceles
editar
Un trapecio tangencial isósceles tiene sus aristas laterales iguales. Dado que un trapecio isósceles es cíclico, un trapecio tangencial isósceles es un cuadrilátero bicéntrico. Es decir, que tiene tanto una circunferencia inscrita como una circunferencia circunscrita.
Si las bases son a y b, entonces el inradio viene dado por[7]
Deducir esta fórmula es un problema que ya aparecía en las tablas Sangaku de Japón, entre los siglos XVII y XIX. Del teorema de Pitot se deduce que las longitudes de las aristas laterales son la mitad de la suma de las bases. Dado que el diámetro del incírculo es la raíz cuadrada del producto de las bases, un trapecio tangencial isósceles ofrece una buena interpretación geométrica de la media aritmética y la media geométrica de las bases como la longitud de una arista lateral y del diámetro del incirculo, respectivamente.
El área K de un trapecio isósceles tangencial con bases a y b viene dada por[8]
Referencias
editar- ↑ a b Josefsson, Martin (2014), «The diagonal point triangle revisited», Forum Geometricorum 14: 381-385.
- ↑ a b H. Lieber and F. von Lühmann, Trigonometrische Aufgaben, Berlin, Dritte Auflage, 1889, p. 154.
- ↑ a b Josefsson, Martin (2010), «Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral», Forum Geometricorum 10: 119-130..
- ↑ a b c J. Wilson, Problem Set 2.2, The University of Georgia, 2010.
- ↑ Chernomorsky Lyceum, Inscribed and circumscribed quadrilaterals, 2010, .
- ↑ a b c «Circle inscribed in a trapezoid, Art of Problem Soving, 2011». Archivado desde el original el 20 de diciembre de 2021. Consultado el 18 de octubre de 2019.
- ↑ MathDL, Inscribed circle and trapezoid, The Mathematical Association of America, 2012, .
- ↑ Abhijit Guha, CAT Mathematics, PHI Learning Private Limited, 2014, p. 7-73.
Datos: Q7682884
