Triangulación de peso mínimo

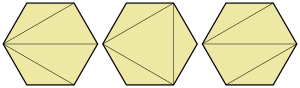
En geometría computacional, se denomina problema de triangulación de peso mínimo (Minimum-weight triangulation o MWT) al problema de encontrar una triangulación de longitud de borde total mínima.^[1] Es decir, dado un polígono de entrada (o el cierre convexo de un conjunto de puntos de la entrada) encontrar la subdivisión del mismo en triángulos adyacentes, de tal manera que se minimice la suma de los perímetros de los triángulos. El problema es NP-duro para entradas consistentes en conjuntos de puntos, pero puede ser aproximado con cualquier grado deseado de exactitud. Si la entrada consiste en un polígono, puede ser solucionado exactamente en tiempo polinómico. La triangulación de peso mínimo también se ha denominado a veces la triangulación óptima.

Historia

El problema de triangulación de peso mínimo de un conjunto de puntos fue propuesto por Düppe y Gottschalk (1970) , quienes sugirieron su aplicación a la construcción de redes irregulares de triángulos para representar contornos terrestres , proponiendo un algoritmo voráz para aproximarlo.Shamos y Hoey (1975) conjeturaron que la triangulación de peso mínimo siempre coincidiría con la triangulación de Delaunay, pero esto fue rápidamente refutado por Lloyd (1977), y de hecho Kirkpatrick (1980) mostró que los pesos de las dos triangulaciones pueden diferir por un factor lineal.^[2]

El problema de triangulación de peso mínimo se hizo notorio cuándo Garey y Johnson (1979) lo incluyeron en una lista de problemas abiertos en su libro sobre completitud NP, y muchos autores posteriores publicaron resultados parciales sobre ello. Finalmente,Mulzer y Rote (2008) demostró que el problema era NP-duro, y Remy y Steger (2009) mostró que es posible construir aproximaciones al mismo de forma eficiente.

Complejidad

El peso de una triangulación de un conjunto de puntos en el plano euclídeo está definido como la suma de longitudes de sus bordes. Su problema de decisión consiste en decidir si existe alguna triangulación de peso inferior a un peso dado. Se demostró que este en un problema NP-duro por Mulzer y Rote (2008), mediante una demostración por reducción de grafo plano 1-EN-3, un caso especial del problema de satisfacibilidad booleana en el que un 3-CNF cuyo grafo es planar es aceptado cuándo satisface la condición un literal en cada cláusula. La demostración empleó ayuda de un ordenador para verificar el comportamiento correcto de la misma.

No es sabido si el problema de triangulación de peso mínimo es NP-completo, ya que este depende del problema aún abierto de determinar si la suma de radicales puede ser computada en tiempo polinómico. Aun así, Mulzer y Rote remarcaron que el problema es NP-completo si los pesos de borde son redondeados a valores enteros.

Cálculo de soluciones aproximadas

La triangulación voraz de un polígono no siempre coincide con la triangulación de peso mínimo, pero es una aproximación calculada en tiempo aceptable.

Varios autores han relacionado el peso de la triangulación de peso mínimo con el de otras triangulaciones que puedan ser usadas en algún algoritmo de aproximación, calculando el cociente entre ambas. En este sentido, es sabido que la triangulación de Delaunay tiene una razón de $\Theta (n)$ ,^[3] y que la triangulación voraz (aquella formada añadiendo en cada paso el borde más corto posible, mediante la unión del par de vértices más próximos siempre que esta no atraviese un borde anterior) tiene una razón de $\Theta ({\sqrt {n}})$ .^[4] En cualquier caso, para nubes de puntos distribuidos aleatoriamente, tanto la triangulación de Delaunay como la voraz están dentro del factor logarítmico del peso mínimo.^[5]

El trabajo de Mulzer y Rote también implica la complejidad NP-Hard de encontrar una solución aproximada que asegure un error inferior a O(1/n²), así que es poco probable que pueda encontrarse un algoritmo que calcule la triangulación de peso mínimo en tiempo polinómico. Sin embargo, es posible una solución cuasi-polinomial: Dada una constante ε > 0, se puede encontrar una solución aproximada con razón 1 + ε en tiempo cuasi-polinomial exp(O((log n)⁹).^[6]

Referencias

↑ Vea descripciones del problema en Xu (1998),Levcopoulos (2008), y De Loera, Rambau y Santos (2010).
↑ See also Manacher y Zobrist (1979).
↑ Kirkpatrick (1980). Una peor aproximación fue calculada en Manacher y Zobrist (1979).
↑ Se publicó una serie de ejemplos demostrando que la razón es $\Omega ({\sqrt {n}})$ en Levcopoulos (1987), y el correspondiente límite superior en Levcopoulos y Krznaric (1998). Para la razón de aproximación de la triangulación de Delaunay, se había publicado un límite en Manacher y Zobrist (1979), que resultó no ser el inferior.
↑ Lingas (1986).
↑ Vea Remy y Steger (2009). Para resultados anteriores en tiempo polinomial, vea Plaisted y Hong (1987) (log-factor approximation) y Levcopoulos y Krznaric (1998) (constant-factor approximation).

Aichholzer, Oswin; Aurenhammer, Franz; Hackl, Thomas; Speckmann, Bettina (2009), «On minimum weight pseudo-triangulations», Computational Geometry Theory and Applications 42 (6-7): 627-631, MR 2519380, doi:10.1016/j.comgeo.2008.10.002 ..
Aichholzer, Oswin; Aurenhammer, Franz; Hainz, Reinhard (1999), «New results on MWT subgraphs», Information Processing Letters 69 (5): 215-219, doi:10.1016/S0020-0190(99)00018-6 ..
Anagnostou, Efthymios; Corneil, Derek (1993), «Polynomial-time instances of the minimum weight triangulation problem», Computational Geometry. Theory and Applications 3 (5): 247-259, MR 1251594, doi:10.1016/0925-7721(93)90016-Y ..
Beirouti, Ronald; Snoeyink, Jack (1998), «Implementations of the LMT heuristic for minimum weight triangulation», Proc. 14th ACM Symposium on Computational Geometry, pp. 96-105, doi:10.1145/276884.276895 ..
Bose, Prosenjit; Devroye, Luc; Evans, William (1996), «Diamonds are not a minimum weight triangulation's best friend», Proc. 8th Canadian Conference on Computational Geometry (CCCG 1996), pp. 68-73 ..
Capp, Kerry; Julstrom, Bryant A. (1998), «A weight-coded genetic algorithm for the minimum weight triangulation problem», Proc. ACM Symposium on Applied Computing, Atlanta, Georgia, United States, pp. 327-331, doi:10.1145/330560.330833 ..
Cheng, Siu-Wing; Golin, Mordecai; Tsang, J. (1995), «Expected case analysis of β-skeletons with applications to the construction of minimum weight triangulations», Proc. 7th Canadian Conference on Computational Geometry (CCCG 1995), pp. 279-284 ..
Cheng, Siu-Wing; Katoh, Naoki; Sugai, Manabu (1996), «A study of the LMT-skeleton», Algorithms and Computation, Lecture Notes in Computer Science 1178, pp. 256-265, doi:10.1007/BFb0009502 ..
Cheng, Siu-Wing; Xu, Yin-Feng (2001), «On β-skeleton as a subgraph of the minimum weight triangulation», Theoretical Computer Science 262 (1–2): 459-471, doi:10.1016/S0304-3975(00)00318-2 ..
De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010), «3.2.3 Greedy and minimum weight triangulations», Triangulations: Structures for Algorithms and Applications, Algorithms and Computation in Mathematics 25, Springer, pp. 102-107, ISBN 978-3-642-12970-4 ..
Dickerson, Matthew T.; Montague, Mark H. (1996), «A (usually?) connected subgraph of the minimum weight triangulation», Proc. 12th ACM Symposium on Computational Geometry, pp. 204-213, doi:10.1145/237218.237364 ..
Düppe, R. D.; Gottschalk, H. J. (1970), «Automatische Interpolation von Isolinien bei willkürlich verteilten Stützpunkten», Allgemeine Vermessungs-Nachrichten 77: 423-426 .. As cited by Mulzer y Rote (2008) and Remy y Steger (2009).
Eppstein, David (1994), «Approximating the minimum weight Steiner triangulation», Discrete and Computational Geometry 11 (2): 163-191, MR 1254088, doi:10.1007/BF02574002 ..
Garey, M. R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, San Francisco, Calif.: W. H. Freeman, Problem OPEN12, p. 288, ISBN 0-7167-1045-5, MR 519066 ..
Gilbert, P. D. (1979), New results in planar triangulations, Report R-850, Urbana, Illinois: Coordinated Science Laboratory, University of Illinois ..
Grantson, M.; Borgelt, C.; Levcopoulos, C. (2005), «Minimum weight triangulation by cutting out triangles», Proc. 16th International Symposium on Algorithms and Computation, pp. 984-994 ..
Gudmundsson, Joachim; Levcopoulos, Christos (2007), «Minimum weight pseudo-triangulations», Computational Geometry Theory and Applications 38 (3): 139-153, MR 2352529, doi:10.1016/j.comgeo.2007.05.004 ..
Heath, L. S.; Pemmaraju, S. V. (1994), «New results for the minimum weight triangulation problem», Algorithmica 12 (6): 533-552, MR 1297812, doi:10.1007/BF01188718 ..
Hoffmann, M.; Okamoto, Y. (2004), «The minimum weight triangulation problem with few inner points», Proc. 1st International Workshop on Parameterized and Exact Computation, pp. 200-212 ..
Hu, Shiyan (2010), «A new asymmetric inclusion region for minimum weight triangulation», Journal of Global Optimization 46 (1): 63-73, MR 2566136, doi:10.1007/s10898-009-9409-z ..
Jahani, M.; Bigham, B.S.; Askari, A. (2010), «An ant colony algorithm for the minimum weight triangulation», International Conference on Computational Science and Its Applications (ICCSA), pp. 81-85, doi:10.1109/ICCSA.2010.38 ..
Keil, J. Mark (1994), «Computing a subgraph of the minimum weight triangulation», Computational Geometry: Theory & Applications 4 (1): 18-26, doi:10.1016/0925-7721(94)90014-0 . (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..
Kirkpatrick, David G. (1980), «A note on Delaunay and optimal triangulations», Information Processing Letters 10 (3): 127-128, MR 566856, doi:10.1016/0020-0190(80)90062-9 ..
Klincsek, G. T. (1980), «Minimal triangulations of polygonal domains», Annals of Discrete Mathematics 9: 121-123, doi:10.1016/s0167-5060(08)70044-x ..
Knauer, Christian; Spillner, Andreas (2006), «A fixed-parameter algorithm for the minimum weight triangulation problem based on small graph separators», Graph-theoretic concepts in computer science, Lecture Notes in Computer Science 4271, Berlin: Springer, pp. 49-57, MR 2290717, doi:10.1007/11917496_5 ..
Kyoda, Yoshiaki; Imai, Keiko; Takeuchi, Fumihiko; Tajima, Akira (1997), «A branch-and-cut approach for minimum weight triangulation», Algorithms and Computation (Singapore, 1997), Lecture Notes in Computer Science 1350, Berlin: Springer, pp. 384-393, MR 1651067, doi:10.1007/3-540-63890-3_41 ..
Lenhart, William; Liotta, Giuseppe (2002), «The drawability problem for minimum weight triangulations», Theoretical Computer Science 270 (1-2): 261-286, MR 1871072, doi:10.1016/S0304-3975(00)00383-2 ..
Levcopoulos, Christos (1987), «An Ω(√n) lower bound for the nonoptimality of the greedy triangulation», Information Processing Letters 25 (4): 247-251, MR 896144, doi:10.1016/0020-0190(87)90170-0 ..
Levcopoulos, Christos (2008), «Minimum Weight Triangulation», en Kao, Ming-Yang, ed., Encyclopedia of Algorithms, Springer, pp. 546-548, ISBN 978-0-387-30770-1 ..
Levcopoulos, C.; Krznaric, D. (1998), «Quasi-greedy triangulations approximating the minimum weight triangulation», Journal of Algorithms 27: 303-338, MR 1622398, doi:10.1006/jagm.1997.0918 ..
Lingas, Andrzej (1986), «The Greedy and Delaunay triangulations are not bad in the average case», Information Processing Letters 22 (1): 25-31, doi:10.1016/0020-0190(86)90038-4 ..
Lingas, Andrzej (1987), «A new heuristic for minimum weight triangulation», SIAM Journal on Algebraic and Discrete Methods 8 (4): 646-658, MR 918066, doi:10.1137/0608053 ..
Lingas, Andrzej (1998), «Subexponential-time algorithms for minimum weight triangulations and related problems», Proceedings of the 10th Canadian Conference on Computational Geometry (CCCG'98) ..
Lloyd, E. (1977), «On triangulations of a set of points in the plane», Proc. 18th IEEE Symposium on Foundations of Computer Science, pp. 228-240 ..
Manacher, Glenn K.; Zobrist, Albert L. (1979), «Neither the greedy nor the Delaunay triangulation of a planar point set approximates the optimal triangulation», Information Processing Letters 9 (1): 31-34, MR 537055, doi:10.1016/0020-0190(79)90104-2 ..
Meijer, Henk; Rappaport, David (1992), «Computing the minimum weight triangulation of a set of linearly ordered points», Information Processing Letters 42 (1): 35-38, MR 1160443, doi:10.1016/0020-0190(92)90129-J ..
Mulzer, Wolfgang; Rote, Günter (2008), «Minimum-weight triangulation is NP-hard», Journal of the ACM 55 (2), Article A11, arXiv:cs.CG/0601002, doi:10.1145/1346330.1346336 ..
Plaisted, D. A.; Hong, J. (1987), «A heuristic triangulation algorithm», Journal of Algorithms 8: 405-437, doi:10.1016/0196-6774(87)90020-4 ..
Qin, Kaihuai; Wang, Wenping; Gong, Minglun (1997), «A genetic algorithm for the minimum weight triangulation», IEEE International Conference on Evolutionary Computation, pp. 541-546, doi:10.1109/ICEC.1997.592370 ..
Remy, Jan; Steger, Angelika (2009), «A quasi-polynomial time approximation scheme for minimum weight triangulation», Journal of the ACM 56 (3), Article A15, doi:10.1145/1516512.1516517 . (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..
Shamos, M. I.; Hoey, D. J. (1975), «Closest-point problems», Proc. 16th IEEE Symposium on Foundations of Computer Science, pp. 151-162 ..
Wang, Cao An; Yang, Boting (2001), «A lower bound for β-skeleton belonging to minimum weight triangulations», Computational Geometry: Theory & Applications 19 (1): 35-46, doi:10.1016/S0925-7721(01)00008-6 ..
Xu, Yin-Feng (1998), «Minimum weight triangulations», Handbook of Combinatorial Optimization, Vol. 2, Boston, MA: Kluwer Academic Publishers, pp. 617-634, MR 1665412 ..
Yang, Bo Ting; Xu, Yin Feng; You, Zhao Yong (1994), «A chain decomposition algorithm for the proof of a property on minimum weight triangulations», en Du, Ding-Zhu; Zhang, Xiang-Sun, eds., Algorithms and Computation: 5th International Symposium, ISAAC '94, Beijing, P. R. China, August 25–27, 1994, Proceedings, Lecture Notes in Computer Science 834, Berlin: Springer, pp. 423-427, MR 1316441, doi:10.1007/3-540-58325-4_207 ..

Enlaces externos

Minimum Weight Triangulation using an LMT Skeleton source code'

Datos: Q6865406

[1] Vea descripciones del problema en Xu (1998),Levcopoulos (2008), y De Loera, Rambau y Santos (2010).

[2] See also Manacher y Zobrist (1979).

[3] Kirkpatrick (1980). Una peor aproximación fue calculada en Manacher y Zobrist (1979).

[4] Se publicó una serie de ejemplos demostrando que la razón es $\Omega ({\sqrt {n}})$ en Levcopoulos (1987), y el correspondiente límite superior en Levcopoulos y Krznaric (1998). Para la razón de aproximación de la triangulación de Delaunay, se había publicado un límite en Manacher y Zobrist (1979), que resultó no ser el inferior.

[5] Lingas (1986).

[6] Vea Remy y Steger (2009). Para resultados anteriores en tiempo polinomial, vea Plaisted y Hong (1987) (log-factor approximation) y Levcopoulos y Krznaric (1998) (constant-factor approximation).

[1]

[2]

[3]

[4]

[5]

[6]