Ángulo hiperbólico

En matemáticas, un ángulo hiperbólico es una figura geométrica que divide a la hipérbola. Las relaciones del ángulo hiperbólico se asemejan a la relación que existe entre un ángulo ordinario y un círculo. El ángulo hiperbólico es definido para una "posición estándar", y se lo asocia con la medida de un intervalo de una rama de una hipérbola.

El ángulo_hiperbólico u es un número real que es el argumento de las funciones hiperbólicas sinh y cosh. Determina un sector hiperbólico (rojo) que tiene un área u. Las ramas del triángulo hiperbólico (amarillo) son proporcionales a sinh(u) y cosh(u).

Superior: Ángulos hiperbólicos positivo y negativo. Inferior: La diferencia entre dos ángulos positivos se muestra como Δu = u₂ − u₁.

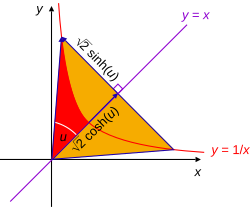
Un ángulo hiperbólico en posición estándar es el ángulo en (0, 0) entre el rayo hasta (1, 1) y el rayo hasta (x, 1/x) donde x > 1.

La magnitud del ángulo hiperbólico es el área del sector hiperbólico correspondiente que vale ln x.

Notar que a diferencia del ángulo circular, el ángulo hiperbólico no se encuentra acotado, tal como sucede con la función ln x, una característica relacionada con la naturaleza no acotada de las series armónicas. El ángulo hiperbólico en posición estándar es considerado negativo cuando 0 < x < 1.

Supóngase que ab = 1 y cd = 1 con c > a > 1 de forma tal que (a, b) y (c, d) determinan un intervalo sobre la hipérbola xy = 1. Entonces el mapeo de compresión con elementos diagonales b y a mapea este intervalo al ángulo hiperbólico en posición estándar que va desde (1, 1) a (bc, ad). De acuerdo a la relación descubierta por Gregoire de Saint-Vincent, el sector hiperbólico determinado por (a, b) y (c, d) tiene la misma área que este ángulo en posición estándar, y la magnitud del ángulo hiperbólico corresponde con esta área.

Las funciones hiperbólicas sinh, cosh, y tanh utilizan el ángulo hiperbólico como su variable independiente porque sus valores pueden ser planteados mediante analogías con las funciones trigonométricas circulares cuando el ángulo hiperbólico define un triángulo hiperbólico. Por lo tanto este parámetro es sumamente útil en el cálculo de una variable real.

Bibliografía

• Janet Heine Barnett (2004) "Enter, stage center: the early drama of the hyperbolic functions", available in (a) Mathematics Magazine 77(1):15–30 or (b) chapter 7 of Euler at 300, RE Bradley, LA D'Antonio, CE Sandifer editors, Mathematical Association of America ISBN 0-88385-565-8 .
• Arthur Kennelly (1912) Application of hyperbolic functions to electrical engineering problems
• William Mueller, Exploring Precalculus, § The Number e, Hyperbolic Trigonometry.
• John Stillwell (1998) Numbers and Geometry exercise 9.5.3, p. 298, Springer-Verlag ISBN 0-387-98289-2.

• Datos: Q1003216