Órbita de halo

Una órbita de halo es una órbita periódica tridimensional cerca de los puntos de Lagrange L₁, L₂ o L₃ en el problema de los tres cuerpos de la mecánica orbital. Aunque el punto de Lagrange es solo un punto en el espacio vacío, se puede estar en órbita alrededor de él. Se puede pensar que las órbitas de halo son el resultado de una interacción entre la atracción gravitatoria de dos cuerpos planetarios y las aceleraciones centrífugas y el efecto Coriolis en una nave espacial. Existen órbitas de halo en cualquier sistema de tres cuerpos, por ejemplo el sistema Sol-Tierra y el sistema Tierra-Luna. Existen "familias" continuas de órbitas de halo tanto de norte como de sur en cada punto de Lagrange. Debido a que las órbitas de halo tienden a ser inestables, se requiere un mantenimiento de posición orbital para tener un satélite en órbita.

Animación de la trayectoria de SOHO.

Vista polar

Vista ecuatorial

Definición e historia

Robert W. Farquhar utilizó por primera vez el nombre "halo" para estas órbitas en su tesis doctoral.^[1] Abogó por el uso de naves espaciales en una órbita de halo en la cara oculta de la Luna (Tierra-Luna L₂) como estación de retransmisión de comunicaciones para una misión Apolo en la cara oculta de la Luna. Una nave espacial en esa órbita de halo tendría una vista ininterrumpida tanto de la Tierra como de la cara oculta de la Luna. Al final, ni un satélite de enlace de comunicación posicionado en L₂, ni una misión conjunta Apolo para un aterrizaje lunar en la cara oculta se hicieron realidad.^[2]

Véase también

Referencias

↑ Farquhar, R. W.: "The Control and Use of Libration-Point Satellites", Ph.D. Dissertation, Dept. of Aeronautics and Astronautics, Stanford University, Stanford, California, 1968
↑ Schmid, P. E. (June 1968). «Lunar Far-Side Communication Satellites» (PDF). NASA. Consultado el 16 de julio de 2008.

Enlaces externos

CDS140B: Computation of Halo Orbit
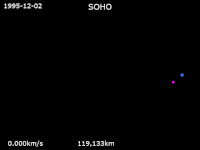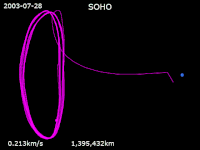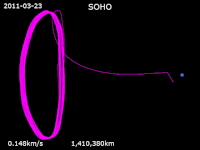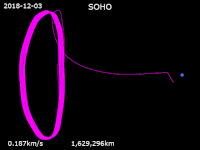
SOHO - The Trip to the L1 Halo Orbit
Low Energy Interplanetary Transfers Using Halo Orbit Hopping Method with STK/Astrogator
Gaia's Lissajous Type Orbit — a Lissajous-type orbit, i.e., a near-circular ellipse or "halo"

Datos: Q1133479

[1] Farquhar, R. W.: "The Control and Use of Libration-Point Satellites", Ph.D. Dissertation, Dept. of Aeronautics and Astronautics, Stanford University, Stanford, California, 1968

[2] Schmid, P. E. (June 1968). «Lunar Far-Side Communication Satellites» (PDF). NASA. Consultado el 16 de julio de 2008.

[1]

[2]