Archivo:Academ Example of similarity with ratio square root of 2.svg
Ver la imagen en su resolución original ((Imagen SVG, nominalmente 600 × 600 pixels, tamaño de archivo: 3 kB))
Resumen
| Descripción |
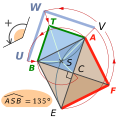
English: One of the two classical squares is the image of the other square under several similarities. Each of them has a ratio equal to √2 or its inverse, because of the ratio 2 or 0,5 between the areas of the squares. As any similarity that is not an isometry, each similarity that transforms one square into the other one has a unique fixed point, called its center. The center of some similarities is a vertex common to the squares. For example, the point A is obviously the center of the indirect similarity that shrinks the triangle EFA into BTA. This drawing shows the direct similarity that shrinks EFA into ATB. Another drawing with the same notations shows the direct similarity with center A, that enlarges the triangle BCA into EFA.
We conceive the direct similarity that transforms AEF into BAT, and B into C, because of four thin red lines. Each of them begins with an arc of 135 degrees that starts from a vertex of ABEF, and finishes by going straight to the image of the start point, and straight toward S. As any direct plane similarity that is not an isometry, the exhibited similarity is the composition of an homothety and a rotation with the same center S. The exhibited homothety has a positive ratio, so its ratio equals the ratio of the similarity: 1/ √2. And the angle of the rotation is + 135 degrees modulo 360 degrees: the angle of the similarity. We can construct the center S of this similarity solely because of its oriented angle + 135 degrees. This point S is the intersection of the two blue quarter-circles. Each of them is drawn inside a square, its center is F or T, and its radius is the dimension of the square: AF or BT. The two legs of the right triangle AEF are drawn in red, and the letters A and F are red. The rotation transforms these red legs into a blue line, and the images of A and F under the rotation are named with blue letters: U and W. The homothety transforms the blue line into a green line: the two legs of the isosceles right triangle BAT. The letters B and T are green.Français : L’un des deux carrés classiques est l’image de l’autre carré par plusieurs similitudes. Chacune d’entre elles a un rapport égal à √2 ou à son inverse, à cause du rapport 2 ou 0,5 entre les aires des deux carrés. Comme toute similitude qui n’est pas une isométrie, chaque similitude qui transforme l’un en l’autre carré a un point invariant unique, appelé son centre. Le centre de certaines similitudes est un sommet commun aux carrés. Par exemple, le point A est évidemment le centre de la similitude indirecte qui réduit le triangle EFA en BTA. Ce dessin montre la similitude directe qui réduit EFA en ATB. Un autre dessin avec les mêmes notations montre la similitude directe de centre A, qui agrandit le triangle BCA en EFA.
On conçoit la similitude directe qui transforme AEF en BAT, et B en C, grâce à quatre fines lignes rouges. Chacune commence par un arc de 135 degrés qui part d’un sommet de ABEF, et se termine en allant tout droit à l’image du point de départ, et tout droit vers S. Comme toute similitude plane directe qui n’est pas une isométrie, la similitude exhibée est la composée d’une homothétie et d’une rotation de même centre S. L’homothétie exhibée a un rapport positif, alors son rapport est égal au rapport de la similitude : 1/ √2. Et l’angle de la rotation est + 135 degrés modulo 360 degrés : l’angle de la similitude. On peut construire le centre S de cette similitude en raisonnant seulement sur son angle orienté + 135 degrés. Ce point S est l’intersection des deux quarts de cercles bleus. Chacun d’eux est tracé à l’intérieur d’un carré, son centre est F ou T, et son rayon est la dimension du carré : AF ou BT. Les deux côtés de l’angle droit du triangle rectangle AEF sont tracés en rouge, et les lettres A et F sont rouges. La rotation transforme ces côtés rouges en une ligne bleue, et les images de A et F par la rotation sont nommées par des lettres bleues : U et W. L’homothétie rétrécit la ligne bleue en une ligne verte : les deux côtés de l’angle droit du triangle rectangle isocèle BAT. Les lettres B et T sont vertes. |
| Fecha | |
| Fuente | Trabajo propio |
| Autor | Yves Arthur Baelde |
| SVG desarrollo |  El código fuente de esta imagen SVG es válido.  Este archivo fue creado con un editor de texto. Su código fuente puede contener información adicional. |
Licencia
- Eres libre:
- de compartir – de copiar, distribuir y transmitir el trabajo
- de remezclar – de adaptar el trabajo
- Bajo las siguientes condiciones:
- atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo.
- compartir igual – En caso de mezclar, transformar o modificar este trabajo, deberás distribuir el trabajo resultante bajo la misma licencia o una compatible como el original.
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 12:49 1 mar 2022 | | 600 × 600 (3 kB) | Arthur Baelde | better framing, lighter colors and other improvements |
| 10:25 18 sep 2011 |  | 625 × 625 (3 kB) | Baelde | code SVG stroke-linejoin="bevel" in element g | |
| 10:21 18 sep 2011 |  | 625 × 625 (3 kB) | Baelde | {{Information |Description ={{en|1=One of the two classical squares is the image of the other square under several similarities. Each of them |
Usos del archivo
La siguiente página usa este archivo:
Uso global del archivo
Las wikis siguientes utilizan este archivo:
- Uso en en.wiki.x.io
- Uso en id.wiki.x.io
- Uso en sr.wiki.x.io
- Uso en ta.wiki.x.io
- Uso en vi.wiki.x.io
- Uso en zh.wiki.x.io
