Wikipedia

Archivo:Random matrix eigenvalues.gif

Ver la imagen en su resolución original (800 × 800 píxeles; tamaño de archivo: 4,7 MB; tipo MIME: image/gif, bucleado, 100 frames, 10s)

Este es un archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia. Más abajo se reproduce su página de descripción con la información sobre su origen y licencia.

Resumen

Descripción
English: Eigenvalues of 4 classes of random matrices on the complex plane. (I am using ~10³ 2x2 matrices, so any central limit theorem valid for large matrices do not really apply here)
Fecha
Fuente https://twitter.com/j_bertolotti/status/1294255802296016898
Autor Jacopo Bertolotti
Permiso
(Reutilización de este archivo)		 https://twitter.com/j_bertolotti/status/1030470604418428929

Mathematica 12.1 code

\[Lambda]random = {};
Do[m = 1/2 (RandomVariate[NormalDistribution[0, 1], {2, 2}] + I RandomVariate[NormalDistribution[0, 1], {2, 2}]);
  AppendTo[\[Lambda]random, Eigenvalues[m]]; , {1000}];
\[Lambda]ortho = {};
Do[m = 1/2 (RandomVariate[NormalDistribution[0, 1], {2, 2}] + I RandomVariate[NormalDistribution[0, 1], {2, 2}]);
  m = Orthogonalize[m]; AppendTo[\[Lambda]ortho, Eigenvalues[m]]; , {1000}];
\[Lambda]symp = {};
Do[m = 1/2 (RandomVariate[NormalDistribution[0, 1], {2, 2}] + I RandomVariate[NormalDistribution[0, 1], {2, 2}]);
  m = m/Sqrt[Det[m]]; AppendTo[\[Lambda]symp, Eigenvalues[m]]; , {1000}];
\[Lambda]herm = {};
Do[m = 1/2 (RandomVariate[NormalDistribution[0, 1], {2, 2}] + I RandomVariate[NormalDistribution[0, 1], {2, 2}]);
  m = (m + ConjugateTranspose[m])/2; AppendTo[\[Lambda]herm, Eigenvalues[m]]; , {1000}];
step[t_] := Ceiling[1000*t^2]
p0 = Table[
   GraphicsGrid[{{
      ListPlot[
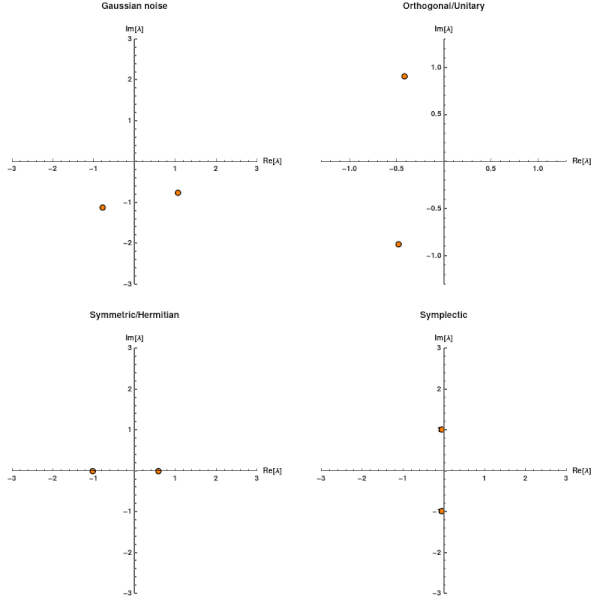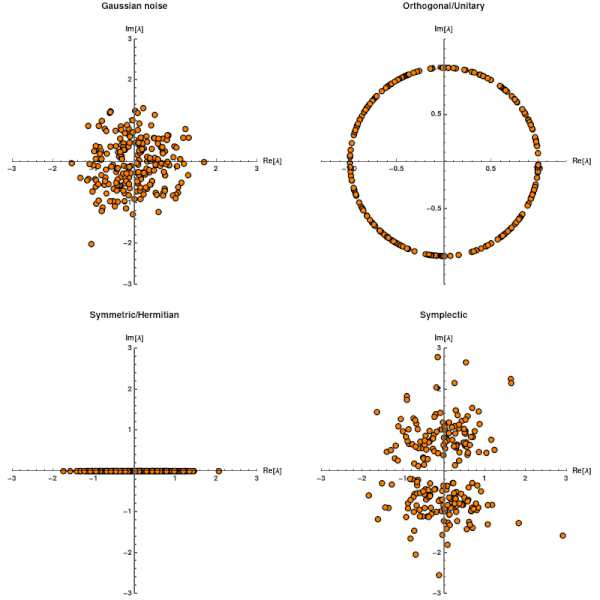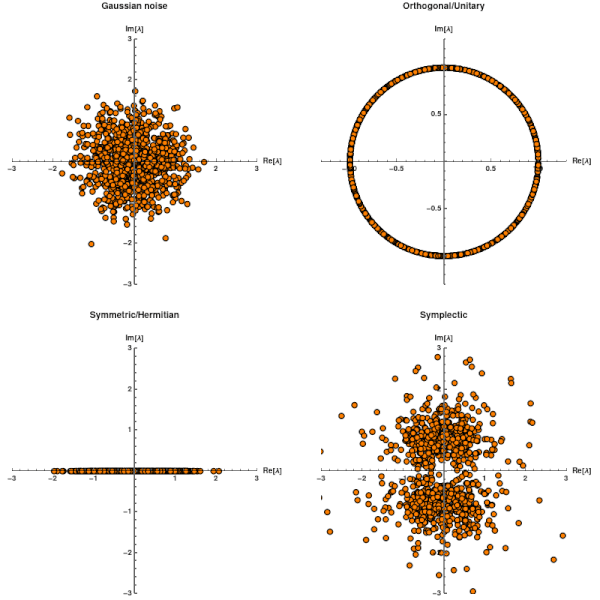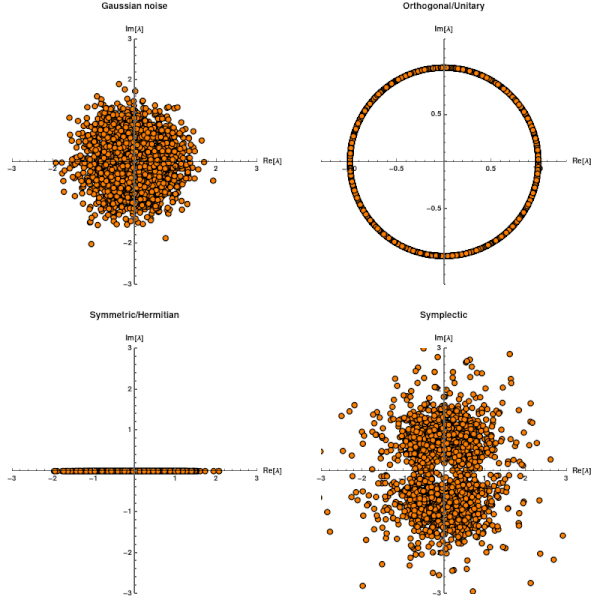
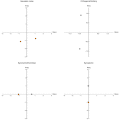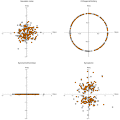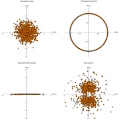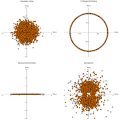
       Evaluate[{Re[#], Im[#]} & /@ Flatten[\[Lambda]random[[1 ;; step[t]]] ] ], PlotRange -> {{-3, 3}, {-3, 3}}, AspectRatio -> 1, AxesStyle -> {Black, Thick}, PlotMarkers -> {Graphics[{Orange, Disk[], Black, Circle[]}], 0.03 }, AxesLabel -> {"Re[\[Lambda]]", "Im[\[Lambda]]"}, LabelStyle -> {Black, Bold}, AxesStyle -> Black, PlotLabel -> "Gaussian noise"]
      ,
      ListPlot[
       Evaluate[{Re[#], Im[#]} & /@ Flatten[\[Lambda]ortho[[1 ;; step[t]]]] ], PlotRange -> {{-1.3, 1.3}, {-1.3, 1.3}}, AspectRatio -> 1, AxesStyle -> {Black, Thick}, PlotMarkers -> {Graphics[{Orange, Disk[], Black, Circle[]}], 0.03 }, AxesLabel -> {"Re[\[Lambda]]", "Im[\[Lambda]]"}, LabelStyle -> {Black, Bold}, AxesStyle -> Black, PlotLabel -> "Orthogonal/Unitary"]
      }, {
      ListPlot[
       Evaluate[{Re[#], Im[#]} & /@ Flatten[\[Lambda]herm[[1 ;; step[t]]]] ], PlotRange -> {{-3, 3}, {-3, 3}}, AspectRatio -> 1, AxesStyle -> {Black, Thick}, PlotMarkers -> {Graphics[{Orange, Disk[], Black, Circle[]}], 0.03 }, AxesLabel -> {"Re[\[Lambda]]", "Im[\[Lambda]]"}, LabelStyle -> {Black, Bold}, AxesStyle -> Black, PlotLabel -> "Symmetric/Hermitian"]
      ,
      ListPlot[
       Evaluate[{Re[#], Im[#]} & /@ Flatten[\[Lambda]symp[[1 ;; step[t]]]] ], PlotRange -> {{-3, 3}, {-3, 3}}, AspectRatio -> 1, AxesStyle -> {Black, Thick}, PlotMarkers -> {Graphics[{Orange, Disk[], Black, Circle[]}], 0.03 }, AxesLabel -> {"Re[\[Lambda]]", "Im[\[Lambda]]"}, LabelStyle -> {Black, Bold}, AxesStyle -> Black, PlotLabel -> "Symplectic"]
      }}, ImageSize -> 800]
   , {t, 0.0001, 1, 0.01}];
ListAnimate[p0]

Licencia

Yo, el titular de los derechos de autor de esta obra, la publico en los términos de la siguiente licencia:
Creative Commons CC-Zero Este archivo está disponible bajo la licencia Creative Commons Dedicación de Dominio Público CC0 1.0 Universal.
La persona que ha asociado una obra a este documento lo dedica al dominio público mediante la cesión mundial de sus derechos bajo la ley de derechos de autor y todos los derechos legales adyacentes propios de dicha, en el ámbito permitido por ley. Puedes copiar, modificar, distribuir y reproducir el trabajo, incluso con objetivos comerciales, sin pedir aprobación del autor.

Leyendas

Añade una explicación corta acerca de lo que representa este archivo
Eigenvalues of 4 classes of random matrices on the complex plane.

Elementos representados en este archivo

representa a

valor propio

matriz aleatoria

plano complejo

Historial del archivo

Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.

Fecha y horaMiniaturaDimensionesUsuarioComentario
actual09:06 17 ago 2020Miniatura de la versión del 09:06 17 ago 2020800 × 800 (4,7 MB)BertoUploaded own work with UploadWizard

La siguiente página usa este archivo:

Uso global del archivo

Las wikis siguientes utilizan este archivo:

Metadatos

Este archivo contiene información adicional, probablemente añadida por la cámara digital o el escáner usado para crearlo o digitalizarlo.

Si el archivo ha sido modificado desde su estado original, pueden haberse perdido algunos detalles.

Obtenido de «https://es.wiki.x.io/wiki/Archivo:Random_matrix_eigenvalues.gif»