Archivo:Uniaxial.png

Tamaño de esta previsualización: 240 × 600 píxeles. Otras resoluciones: 96 × 240 píxeles · 192 × 480 píxeles.

Ver la imagen en su resolución original (800 × 2000 píxeles; tamaño de archivo: 26 kB; tipo MIME: image/png)

Esta imagen debería volverse a crear como imágenes vectoriales SVG. Esto proporciona muchas ventajas, véase Commons:Media for cleanup (en inglés) para más información. Si ya hay una versión SVG de esta imagen disponible, por favor súbala a Commons. Tras subirla, reemplace esta plantilla con la plantilla {{vector version available|nuevo nombre de imagen.svg}} en esta imagen.

Resumen

Author: en:user:AndrewKepert
Toolchain: MetaPost and TeX.
Source: below
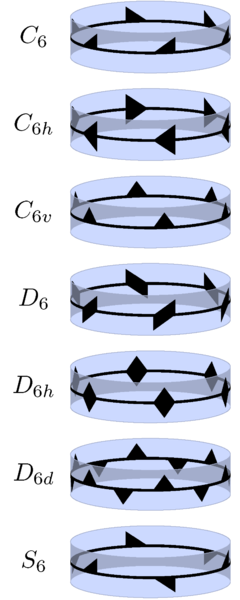
Description: Illustration of a typical member of each of 7 infinite families of 3D point groups.
Destination: en:Point groups in three dimensions.
Permission: GFDL / CC

Source code

Instructions: on a system with a modern TeTeX or similar installed save the following two files, then run

mpost uniaxial && pdftex uniaxial

You will then need to use ghostscript or similar to make a raster image out of the pdf.

Source code author: en:user:AndrewKepert

Source code license: GPL

Este PNG gráfico fue creado con MetaPost

Código fuente

PostScript code

picture pic[];
 pair pt[],pt[]n,pt[]e,pt[]w,pt[]s,pt[]ne,pt[]nw,pt[]se,pt[]sw;
 pair ux,uy,uz;
 path unitcircle; unitcircle=fullcircle scaled 2;
 boolean front[];
 color colour[];
 path p[];
 
 u=16;
 ux=.4*down*u;
 uy=right*2u;
 uz=up*.5u;
 
 transform xyplane[];
 (0,0) transformed xyplane0 = (0,0);
 (1,0) transformed xyplane0 = ux;
 (0,1) transformed xyplane0 = uy;
 for i = -1 step 1/16 until 1:
     xyplane[i]=xyplane[0] shifted (i*uz);
 endfor
 
 theta=10;
 alpha=8;
 
 N:=6;
 
 for i = -1 step .5 until N+1:
     pt[i]   = right rotated  theta        rotated (360i/N) transformed xyplane0;
     front[i]= ypart pt[i] < ypart xyplane0;
     pt[i]e  = right rotated (theta+alpha) rotated (360i/N) transformed xyplane0;
     pt[i]w  = right rotated (theta-alpha) rotated (360i/N) transformed xyplane0;
     pt[i]n  = right rotated  theta        rotated (360i/N) transformed xyplane[.75];
     pt[i]ne = right rotated (theta+alpha) rotated (360i/N) transformed xyplane[.75];
     pt[i]nw = right rotated (theta-alpha) rotated (360i/N) transformed xyplane[.75];
     pt[i]s  = right rotated  theta        rotated (360i/N) transformed xyplane[-.75];
     pt[i]se = right rotated (theta+alpha) rotated (360i/N) transformed xyplane[-.75];
     pt[i]sw = right rotated (theta-alpha) rotated (360i/N) transformed xyplane[-.75];
 endfor
 
 t0=directiontime uz of (unitcircle transformed xyplane0);
 t1=directiontime -uz of (unitcircle transformed xyplane0);
 t2=t0+length unitcircle;
 
 path backface,frontface;
 backface:=(subpath (t0,t1) of unitcircle transformed xyplane[1])
         -- (subpath (t1,t0) of unitcircle transformed xyplane[-1])
         -- cycle;
 frontface:= (subpath (t1,t2) of unitcircle transformed xyplane[1])
         -- (subpath (t2,t1) of unitcircle transformed xyplane[-1])
         -- cycle;
 
 colour0:=(.8,.85,1);
 colour1:=.8[black,colour0];
 colour2:=.6[black,colour1];
 
 def constructribbon(expr delta)=
     % stuff on back face
     pic1:=image( for i = 0 step delta until N-eps: if not front[i]: fill p[i]; fi endfor
         fill (subpath (t0,t1) of unitcircle transformed xyplane[1/16])
         -- (subpath (t1,t0) of unitcircle transformed xyplane[-1/16])
         -- cycle;);
     % stuff on front face
     pic2:=image( for i = 0 step delta until N-eps: if  front[i]: fill p[i]; fi endfor
         fill (subpath (t1,t2) of unitcircle transformed xyplane[1/16])
         -- (subpath (t2,t1) of unitcircle transformed xyplane[-1/16])
         -- cycle;);
     % all of back face
     pic0:=image(fill frontface withcolor colour0;
         fill backface withcolor colour1;
         draw pic1 withcolor colour2);
     fill backface withcolor colour0;
     fill frontface withcolor colour0;
     draw pic1;
     clip pic0 to frontface;
     draw pic0;
     draw pic2;
     draw unitcircle transformed xyplane[1] withpen pencircle scaled 0.2 withcolor colour1;
     draw subpath (t2,t1) of unitcircle transformed xyplane[-1] withpen pencircle scaled 0.2 withcolor colour1;
 enddef;
 
 beginfig(1)
     for i=0 upto N-1:
         p[i]:= pt[i]--pt[i]w--pt[i]ne--pt[i]e--cycle;
     endfor
     constructribbon(1);
 endfig;
 
 beginfig(2)
     for i=0 upto N-1:
         p[i]:=  pt[i]w--pt[i]ne--pt[i]se--cycle ;
     endfor
     constructribbon(1);
 endfig;
 
 beginfig(3)
     for i=0 upto N-1:
         p[i]:= pt[i]--pt[i]e--pt[i]n--pt[i]w--cycle ;
     endfor
     constructribbon(1);
 endfig;
 
 beginfig(4)
     for i=0 upto N-1:
         %p[i]:=  pt[i]--pt[i]ne--pt[i]e--pt[i]--pt[i]sw--pt[i]w--cycle ;
         p[i]:=          pt[i]ne--pt[i]e--       pt[i]sw--pt[i]w--cycle ;
     endfor
     constructribbon(1);
 endfig;
 
 beginfig(5)
     for i=0 upto N-1:
         p[i]:=  pt[i]n--pt[i]e--pt[i]s--pt[i]w--cycle ;
     endfor
     constructribbon(1);
 endfig;
 
 beginfig(6)
     for i=0 upto N-1:
         p[i]:=  pt[i]--pt[i]e--pt[i]n--pt[i]w--cycle ;
         p[i+.5]:=  pt[i+.5]--pt[i+.5]e--pt[i+.5]s--pt[i+.5]w--cycle ;
     endfor
     constructribbon(1/2);
 endfig;
 
 beginfig(7)
     for i=0 upto N-1:
         if odd i:
             p[i]:= pt[i]--pt[i]w--pt[i]ne--pt[i]e--cycle;
         else:
             p[i]:= pt[i]--pt[i]w--pt[i]se--pt[i]e--cycle;
         fi
     endfor
     constructribbon(1);
 endfig;
 
 
 bye

Data

\input supp-pdf
 {\tabskip=5pt  \lineskiplimit=5pt  \lineskip=\lineskiplimit
 \halign{\hfil#\hfil&\hfil$\vcenter{\convertMPtoPDF{#}{1}{1}}$\hfil\cr
     $C_6$&uniaxial.1\cr
     $C_{6h}$&uniaxial.2\cr
     $C_{6v}$&uniaxial.3\cr
     $D_6$&uniaxial.4\cr
     $D_{6h}$&uniaxial.5\cr
     $D_{6d}$&uniaxial.6\cr
     $S_6$&uniaxial.7\cr
     }
 }
 \bye

Licencia

Yo, titular de los derechos de autor de esta obra, la publico en los términos de las siguientes licencias:

Se autoriza la copia, distribución y modificación de este documento bajo los términos de la licencia de documentación libre GNU, versión 1.2 o cualquier otra que posteriormente publique la Fundación para el Software Libre; sin secciones invariables, textos de portada, ni textos de contraportada. Se incluye una copia de la dicha licencia en la sección titulada Licencia de Documentación Libre GNU.

	Este archivo se encuentra bajo la licencia Creative Commons Genérica de Atribución/Compartir-Igual 3.0.

	Eres libre: de compartir – de copiar, distribuir y transmitir el trabajo de remezclar – de adaptar el trabajo Bajo las siguientes condiciones: atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo. compartir igual – En caso de mezclar, transformar o modificar este trabajo, deberás distribuir el trabajo resultante bajo la misma licencia o una compatible como el original.
	Esta etiqueta de licencia fue agregada a este archivo como parte de la actualización de la licencia GFDL.CC BY-SA 3.0truetrue

Este archivo se encuentra bajo la licencia Creative Commons de Atribución/Compartir-Igual 2.5 Genérica, 2.0 Genérica y 1.0 Genérica.

Eres libre:

de compartir – de copiar, distribuir y transmitir el trabajo
de remezclar – de adaptar el trabajo

Bajo las siguientes condiciones:

atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo.
compartir igual – En caso de mezclar, transformar o modificar este trabajo, deberás distribuir el trabajo resultante bajo la misma licencia o una compatible como el original.

Puedes usar la licencia que prefieras.

Historial del archivo

Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.

	Fecha y hora	Miniatura	Dimensiones	Usuario	Comentario
actual	08:28 5 jul 2006		800 × 2000 (26 kB)	AndrewKepert~commonswiki	Author: user:en:AndrewKepert Toolchain: MetaPost and TeX. Source: will be uploaded Description: Illustration of a typical member of each of 7 infinite families of 3D point groups. Destination: en:Point groups in three dimensions. Permission: GF

Usos del archivo

La siguiente página usa este archivo:

Grupos de puntos en tres dimensiones

Uso global del archivo

Las wikis siguientes utilizan este archivo:

Uso en en.wiki.x.io
- Point groups in three dimensions
Uso en id.wiki.x.io
- Pengguna:Klasüo/bak pasir/Arsip 15
- Grup titik dalam tiga dimensi
Uso en nl.wiki.x.io
- Symmetriegroep
Uso en ru.wiki.x.io
- Точечная группа в трёхмерном пространстве
Uso en zh.wiki.x.io
- 三維點群

Archivo:Uniaxial.png

Sumario

Resumen

Source code

PostScript code

Data

Licencia

Leyendas

Elementos representados en este archivo

representa a

estatus de los derechos de autor

bajo derechos de autor

licencia

Creative Commons — Atribución-CompartirIgual 1.0 Genérica

Licencia de documentación libre de GNU, versión 1.2 o posterior

Creative Commons — Atribución-CompartirIgual 2.0 Genérica

Creative Commons — Atribución-CompartirIgual 2.5 Genérica

CC-BY-SA 3.0

Historial del archivo

Usos del archivo

Uso global del archivo