Arcocoseno

En trigonometría el arcocoseno está definido como la función inversa del coseno de un ángulo. Si tenemos: $\arccos \alpha \,$, su significado geométrico es el arco cuyo coseno es alfa.

Función arcocoseno
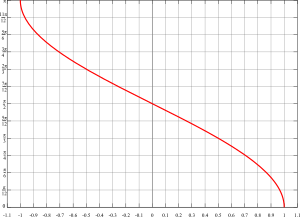Gráfica de Función arcocoseno
Definición	$\textstyle f{\mbox{ tal que }}f(\cos(x))=x\,$
Tipo	Trigonométrica inversa
Dominio	$\textstyle [-1,1]$
Codominio	$\textstyle [0,\pi ]$
Imagen	$\textstyle [0,\pi ]$
Propiedades	Estrictamente decreciente Biyectiva en su dominio
Cálculo infinitesimal
Derivada	$-{\frac {1}{\sqrt {1-x^{2}}}}$
Función inversa	$\textstyle \cos(x)\quad x\in [0,\pi ]$
Funciones relacionadas	arcoseno arcotangente

La función coseno no es biyectiva, por lo que no tiene inversa. Es posible aplicarle una restricción del dominio de modo que se vuelva inyectiva y sobreyectiva. Por convención es preferible restringir el dominio de la función coseno al intervalo $\left[0,\pi \right]$.

Notación

La notación matemática del arcocoseno es arccos; es común la escritura ambigua cos^-1. En diversos lenguajes de programación se suele utilizar la forma ACOS y ACS.

Propiedades

Función recíproca trigonométrica.

El arcocoseno de una función continua es estrictamente decreciente, definida por todo el valor del intervalo $\left[-1,1\right]$:

${\begin{array}{lccl}\arccos :&[-1,1]&\rightarrow &[0,\pi ]\\&x&\rightarrow &y=\arccos(x)\end{array}}$

Su gráfico es simétrico respecto al punto $\left(0,{\frac {\pi }{2}}\right)$, siendo:

$\arccos x=\pi -\arccos(-x)$

La derivada de la función arcocoseno es

${\frac {d}{dx}}\arccos x=-{\frac {1}{\sqrt {1-x^{2}}}}$

Por medio de la guía descrita simétrica vale la relación por argumentos negativos:

$\arccos \left(-x\right)=\pi -\arccos x$

Es posible combinar la suma o diferencia de arcocoseno en una expresión donde el arcocoseno figura una rotación:

$\arccos x_{1}+\arccos x_{2}={\begin{cases}\arccos \left(x_{1}x_{2}-{\sqrt {1-x_{1}^{2}}}{\sqrt {1-x_{2}^{2}}}\right)&x_{1}+x_{2}\geq 0\\2\pi -\arccos \left(x_{1}x_{2}-{\sqrt {1-x_{1}^{2}}}{\sqrt {1-x_{2}^{2}}}\right)&x_{1}+x_{2}<0\end{cases}}$

$\arccos x_{1}-\arccos x_{2}={\begin{cases}-\arccos \left(x_{1}x_{2}+{\sqrt {1-x_{1}^{2}}}{\sqrt {1-x_{2}^{2}}}\right)&x_{1}\geq x_{2}\\\arccos \left(x_{1}x_{2}+{\sqrt {1-x_{1}^{2}}}{\sqrt {1-x_{2}^{2}}}\right)&x_{1}<x_{2}\end{cases}}$

Serie de potencias

El desarrollo en serie de potencias del arcocoseno viene dado por:

${\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}={\frac {\pi }{2}}-x-{\frac {1}{6}}x^{3}+...$

Nótese que este desarrollo solo es válido cuando se expresa el ángulo en radianes.

Demostración

Aplicando el desarrollo en serie de Taylor es sencillo demostrar el siguiente desarrollo: ${\frac {1}{\sqrt {1-t}}}=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}}}t^{n}$ Efectuando el cambio t=s² se obtiene este desarrollo: ${\frac {1}{\sqrt {1-s^{2}}}}=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}}}s^{2n}$ Dado que: $\arccos(x)={\frac {\pi }{2}}-\int _{0}^{x}{\frac {1}{\sqrt {1-s^{2}}}}ds$ Integrando término a término la segunda serie se obtiene el desarrollo en serie del arcocoseno: $\arccos(x)={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}$

Aplicaciones

En un triángulo rectángulo, el arcocoseno equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre su cateto adyacente y la hipotenusa.

Véase también

• Trigonometría
• Identidad trigonométrica

Enlaces externos

• Weisstein, Eric W. «Arcocoseno». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q720341
• Multimedia: Arc cosine function / Q720341