Arista de corte
En teoría de grafos, una arista de corte, puente[1] o istmo[2] es una arista que al ser eliminada en un grafo incrementa el número de componentes conexas de este.[1] Equivalentemente, una arista es un puente si y sólo si no está contenida en ningún ciclo.
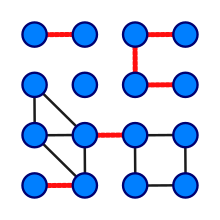
El concepto de arista de corte se puede generalizar a un conjunto de aristas. Así, un corte de aristas-l o corte de líneas-l es un conjunto de l aristas que si se quitan, desconectan el grafo. Por lo tanto, una arista de corte es un corte de aristas-1.[1]
Análogamente, un vértice de corte o punto de corte, es un vértice que al eliminarse incrementa el número de componentes conexos del grafo. La conectividad de un grafo se puede calcular en términos del número de aristas o vértices de corte que posee. Esta conectividad es una medida de su cohesión o robustez.[1]
Un importante problema abierto que involucra puentes es la conjetura del ciclo de doble cobertura,[3] propuesta por Seymour y Szekeres (1978 y 1979, independientemente), que establece que todo grafo sin puentes admite un conjunto de ciclos que contiene cada arista exactamente dos veces.
Aplicaciones
editarEn análisis de redes sociales, un puente o arista de corte es considerada una conexión o lazo interpersonal crucial entre dos actores.[1]
Véase también
editarReferencias
editar- ↑ a b c d e Wasserman y Faust, 2013, «Grafos y matrices» (por Dawn Iacobucci), pp. 121-188.
- ↑ Recuero, A. (1994). «Aplicaciones de la teoría de grafos: búsqueda de caminos en una red y análisis de su conectividad». Informes de la construcción (CSIC) 46 (433). doi:10.3989/ic.1994.v46.i433.1115.
- ↑ «The Cycle Double Cover Conjecture». Archivado desde el original el 20 de julio de 2011. Consultado el 16 de junio de 2008.
Bibliografía
editar- Wasserman, Stanley; Faust, Katherine (2013) [1994]. Análisis de redes sociales: Métodos y aplicaciones. Madrid: Centro de Investigaciones Sociológicas. ISBN 978-84-7476-631-8. OCLC 871814053.