Canteado (geometría)
En geometría, un canteado es un truncamiento de segundo orden en cualquier dimensión que bisela las aristas y los vértices de un politopo regular, creando una nueva faceta en lugar de cada arista y de cada vértice del politopo original.[1] También se aplica a los teselados regulares y a los panales. Así mismo, cantear es rectificar una rectificación.
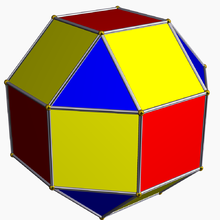

El canteado (para poliedros y teselados) también es denominado expansión en la notación utilizada por Alicia Boole Stott: corresponde a alejar las caras de la forma regular del centro y rellenar una nueva cara en el espacio para cada arista y para cada vértice descubiertos.
Notación
editarUn politopo canteado está representado por un símbolo de Schläfli prolongado t0,2{p,q,...} o r' o rr {p,q,...}.
Para poliedros, un canteado permite mostrar una secuencia directa desde un poliedro regular a su dual.
Ejemplo: secuencia de canteados entre cubo y octaedro:
Ejemplo: un cuboctaedro (figura del centro) es un tetraedro canteado.
Para politopos de mayor dimensión, un canteado ofrece una secuencia directa desde un politopo regular hasta su forma birrectificada.
Ejemplos: canteado de poliedros y teselados
editar| Forma | Poliedros | Teselados | |||
|---|---|---|---|---|---|
| Coxeter | rTT | rCO | rID | rQQ | rHΔ |
| Notación de Conway |
eT | eC= eO | eI= eD | eQ | eH= eΔ |
| Poliedro a expandir |
Tetraedro | Cubo u octaedro |
Icosaedro o dodecaedro |
Teselado cuadrado | Teselado hexagonal Teselado triangular |
| Imagen | |||||
| Animación | |||||
| Coxeter | rrt{2,3} | rrs{2,6} | rrCO | rrID |
|---|---|---|---|---|
| Notación de Conway |
eP3 | eA4 | eaO= eaC | eaI= eaD |
| Poliedros a expandir |
Prisma triangular o bipirámide triangular |
Antiprisma cuadrado o trapezoedro tetragonal |
Cuboctaedro o rombododecaedro |
Icosidodecaedro o triacontaedro rómbico |
| Imagen | ||||
| Animación |
Véase también
editarReferencias
editar- ↑ Mircea Vasile Diudea (2017). Multi-shell Polyhedral Clusters. Springer. pp. 25 de 442. ISBN 9783319641232. Consultado el 27 de octubre de 2022.
Bibliografía
editar- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Enlaces externos
editar- Weisstein, Eric W. «Expansion». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.