Circuito de conmutación
En electricidad y electrónica, las leyes del álgebra de Boole [1] y de la lógica binaria, pueden estudiarse mediante circuitos de conmutación. Un circuito de conmutación estará compuesto por una serie de conmutadores o de interruptor [2] que representarán las variables lógicas de entrada y una o varias cargas que representarán las variables lógicas o funciones de salida.

|

|

|

|

|

|

|

|
|
|

|
|

|

|

|

|
|

|
|

|

|

|

|

|
Los contactos pueden ser normalmente abiertos (NA) o normalmente cerrados (NC). Los primeros permanecerán abiertos mientras no se actúe sobre ellos (por ejemplo al pulsar sobre interruptor, saturar un transistor, etc.). Los contactos NC funcionarán justamente al contrario. Esto significa que si se actúa sobre un contacto NA se cerrará y si se hace sobre uno NC se abrirá.
Conceptos básicos
editarLos circuitos de conmutación se basan en interruptores que permiten o no la circulación de una corriente eléctrica, estos interruptores pueden ser manuales si se actúan directamente, como un interruptor de la luz, por ejemplo; eléctricos: relés o contactores, si su actuación es electro-mecánica, o electrónicos, transistores o puertas lógicas, si se basan en la tecnología electrónica.
Por sencillez, representaremos un interruptor o conmutador por sus contactos eléctricos, si un interruptor conecta dos puntos a y b, diremos que está abierto si no permite la circulación eléctrica entre esos dos puntos: a y b. Diremos que está cerrado si permite la circulación eléctrica entre esos dos puntos.
Un interruptor diremos que esta normalmente abierto (NA) si cuando no se actúa sobre él está abierto, a la posición normal también se le denomina posición de reposo, que el interruptor tendrá normalmente por la actuación de un muelle o resorte que lo lleva a esa posición.
Cuando se actúa sobre un interruptor normalmente abierto (NA), el interruptor se cierra, permitiendo la circulación eléctrica a su través.
Venciendo la fuerza ejercida por el muelle o resorte, y dando lugar al contacto eléctrico entre sus terminales.
En la figura se representa un pulsador normalmente abierto, en reposo en la parte superior, con el muelle en reposo y sus contactos separados, en la parte inferior se ve ese mismo pulsador actuado, con el muelle comprimido y sus terminales eléctricos en contacto, permitiendo la circulación eléctrica entre los puntos a y b.
Si entre dos puntos a y b, colocamos un interruptor normalmente cerrado (NC), que cuando no se actúa sobre él está cerrado, en este caso, la relajación del muelle o resorte da lugar a poner en contacto los terminales eléctricos del interruptor, permitiendo la circulación eléctrica a su través, el interruptor está cerrado. Si actuamos sobre él venciendo la acción del muelle, separando los contactos, el interruptor se abre, no permitiendo la circulación eléctrica. En estos interruptores el resultado es el contrario de la acción, si actuamos sobre el interruptor el interruptor se abre, cortando el paso de la corriente eléctrica, si no actuamos sobre el, se cierra permitiendo la circulación eléctrica.
Como se ha visto, los interruptores pueden ser actuados manualmente, o mecánicamente mediante fines de carrera, presostatos u otros elementos que partiendo de una acción exterior den lugar a una conexión o desconexión eléctrica.
Pero un circuito puede actuar sobre otro circuito, mediante relés o contactores, de modo que podemos disponer de un circuito de conmutación, cuyo resultado es la actuación sobre otro circuito, en estos casos la presencia o no de una corriente eléctrica da lugar a la modificación del estado de un interruptor, que pasara de su posición de reposo a la de actuado.
En la figura podemos ver, una serie de interruptores de este tipo. La actuación sobre ellos se hace mediante un solenoide, que genera un campo magnético y que desplaza el núcleo ferromagnético de la armadura, venciendo al muelle, y cambiando los contactos eléctricos. Cuando la corriente eléctrica no actúa, el muelle eleva al interruptor a la posición de reposo.
Convenio de representación
editarEn un circuito de conmutación se realiza un análisis de la lógica del circuito, haciendo abstracción de los detalles de funcionamiento de los mecanismos que intervienen, así como del dimensionado de los aparatos y resto del circuito para las intensidades de corriente y diferencia de potencial con los que trabaja, prestando atención prioritaria a la lógica de la conmutación, por ello no son necesarios, algunos de los detalles eléctricos, propios de los circuitos eléctricos, y si es necesario determinar un convenio de representación de los circuitos que impida errores en su interpretación, teniendo en cuenta lo siguiente:
- Circuito de conmutación, es un esquema de funcionamiento y no un plano de construcción, por lo tanto la situación de los aparatos se hará según esa lógica.
- En un circuito de conmutación no se señalan detalles eléctricos, como intensidades o tensiones eléctricas.
- Los aparatos se representan siempre en su posición de reposo, aunque estén conectados directamente a una fuente de energía.
- La actuación de los interruptores es siempre de arriba hacia abajo, la posición de reposo es la más alta y la actuada la más baja.
Componentes para un circuito de interruptores.
editar| Figura 1 |
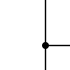
Se deberán de tener en cuenta los siguientes convenios (ver Figura 1):
- Un contacto NA representa una variable conmutable
- Un contacto NC representa una variable lógica negada (A').
- Un circuito cerrado se considera un uno lógico (1).
- Un circuito abierto se considera un cero lógico (0).
- Si no se actúa sobre un contacto se considera que la variable que representa es 0.
- Si se actúa sobre un contacto se considera que la variable que representa es 1.
- Si la carga no se excita la función se considera 0 (por ejemplo una lámpara apagada).
- Si la carga se excita la función se considera 1 (lámpara encendida).
Interruptor múltiple
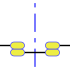
editar| Figura 2 |
Un interruptor múltiple, es el que con solo un mando mueve varios contactos simultáneamente, este tipo de interruptor, no tan sencillo, se emplea para conmutar varios circuitos al mismo tiempo, electivamente separados.
Este tipo de interruptor puede tener contactos directos e inversos, en la figura los dos primeros son directos y el tercero inverso, que a su vez pueden ser de distinta sección, según la intensidad de corriente que circule por cada uno de ellos.
El relé
editarUn relé o Contactor, es un interruptor automático controlado eléctricamente, de este modo una señal eléctrica da lugar a nuevos contactos que, a su vez, alimentan o dejan de alimentar otros circuitos.
En la figura, se puede ver la representación esquemática de un relé. Los contactos se representan en reposo, en la posición que tendrían cuando la bobina no está alimentada; cuando recibe tensión, la armadura se desplaza, cambiando la posición de los contactos.
Circuito en serie
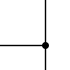
editar| Figura 3 |
De este modo la Figura 3 representa la función lógica Y (AND), esto es, L=a·b· ... ·n. De acuerdo con la tabla de verdad de dicha función, El circuito está cerrado solo si cada uno de los interruptores que intervienen está cerrados.
Circuito en paralelo
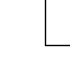
editar| Figura 4 |
Del mismo modo la Figura 4 representa la función lógica O (OR), esto es, L= a+b+ ... +n; y de acuerdo con su tabla de verdad, el circuito está cerrado si al menos uno de los interruptores está cerrado.
Conmutador
editar| Figura 5 |
El conmutador está formado por un interruptor directo y otro inverso, ver Figura 5, que actúan conjuntamente, de modo que con una sola actuación se aísla un circuito y se conecta otro, conmutando los dos circuitos.
En la figura puede verse que la conexión de la izquierda está conectada con la inferior de la derecha cuando a no está actuado.
Si a esta actuada la salida es por la conexión superior de la derecha.
| Figura 6 |
Dos conmutadores conectados según la Figura 6, da como resultado un circuito, que está abierto o cerrado alternativamente, con tan solo modificar uno de los dos conmutadores, si los dos están en la misma posición el circuito está conectado, si se modifica uno cualesquiera de los dos, se desconecta, que volverá a conectarse al actuar sobre uno de ellos, sin importar cual. este circuito se utiliza comúnmente para el encendido de luces en escaleras o la operación desde dos puntos distintos. también es llamada three way o tres vías.
Interruptor de cruce
editar| Figura 7 | |||||
| Figura 8 |
Un interruptor de cruce permuta las dos líneas de entrada (a, b) con las dos de salida (c, d), en las figuras 7 y 8, se pueden ver dos esquemas equivalentes de este tipo de interruptor.
En una posición se conecta a con c y b con d y en la otra se permutan conectándose a con d y c con b.
En estas dos figuras se puede apreciar perfectamente, que distintas distribuciones de los aparatos y distintos cableados pueden dar lugar a los mismos resultados.
Oscilador electromecánico
editarLa construcción de un Oscilador, con medios exclusivamente electromecánicos, se hace sencillamente, conectando la bobina de un relé a uno de sus contactos normalmente conectados (NC), cuando el relé se excita, el contacto (NC) se desconecta, desconectando la bobina, que da lugar a que el contacto (NC) entre en contacto de nuevo.
Este es el mecanismo en el que se basa el timbre eléctrico clásico.
Sistema combinacional
editarEn teoría de autómatas un sistema combinacional es un sistema lógico basado en el álgebra de Boole, tanto en tecnología electrónica como electromecánica. Podemos ver una implementación en conmutadores, de sistemas combinacionales, ordenando por el número de variables que intervienen.
Número de combinaciones
editarPartiendo de un número n de variables, cada una de las cuales puede tomar el valor verdadero: 1, o falso: 0, por combinatoria, podemos saber que el número total de combinaciones: C, que se pueden presentar es:
el número de combinaciones que se pueden dar con n variable, cada una de las cuales puede tomar uno entre dos valores lógicos es de dos elevado a n, esto es, el número de combinaciones: C, tiene crecimiento exponencial respecto al número de variable n:
Si consideramos que un sistema combinacional de n variables binarias, puede presentar un resultado verdadero: 1, o falso: 0, para cada una de las posibles combinaciones de entrada tenemos que se pueden construir un número de funciones: F con n variables de entrada, donde:
Que da como resultado la siguiente tabla:
Para componer una tabla de verdad, pondremos las n variables en una línea horizontal, debajo de estas variables desarrollamos las distintas combinaciones que se pueden formar con 1 y 0, dando lugar a las distintas C, número de combinaciones. Normalmente solo se representa la función para la que se confecciona la tabla de verdad, y en todo caso funciones parciales que ayuden en su cálculo, en la figura, se pueden ver todas las funciones posibles F, que pueden darse para el número de variables dado.
Así podemos ver que para dos variables binarias: a y b, n= 2 , que pueden tomar los valores 1 y 0, se pueden desarrollar cuatro combinaciones: C= 4, con estos valores se pueden definir dieciséis resultados distintos, F= 16, cada una de las cuales sería una función de dos variables binarias. Para otro número de variables se obtendrán los resultados correspondientes, dado el crecimiento exponencial de F, cuando n toma valores mayores de cuatro o cinco, la representación en un cuadro resulta compleja, y si se quiere representar las combinaciones posibles F, resulta ya complejo para n= 3.
Tabla de verdad de cero variables
editar- n= 0
- C= 1
- F= 2
Caso: 1.
editarEsta función se denomina tautología y presenta el resultado verdadero (1) en todos los casos.
Esta función se representa:
Estas funciones son equivalentes:
Caso: 2.
editarEsta función se denomina contradicción y presenta el resultado falso(0) en todos los casos.
Esta función se representa:
Estas funciones son equivalentes:
Tabla de verdad de una variable
editar- n= 1
- C= 2
- F= 4
Caso: 1.
editarEsta función se denomina tautología y presenta el resultado verdadero (1) en todos los casos.
Esta función se representa:
Estas funciones son equivalentes:
Caso: 2.
editarEsta función se denomina: afirmación lógica, asigna a la función el mismo valor lógico que tiene la variable.
Esta función se representa:
Caso: 3.
editarEsta función se denomina: negación lógica, asigna a la función el valor lógico opuesto al que tiene la variable.
Esta función se representa:
Caso: 4.
editarEsta función se denomina contradicción y presenta el resultado falso(0) en todos los casos.
Esta función se representa:
Estas funciones son equivalentes:
Tabla de verdad de dos variables
editar- n= 2
- C= 4
- F= 16
Caso: 1.
editarEsta función se una tautología y presenta el resultado verdadero(1) en todos los casos.
Esta función se representa:
Estas funciones son equivalentes:
Caso: 2.
editarEsta función se denomina: Disyunción lógica, y presenta el resultado falso(0) solo cuando las dos variablea: a, b; son falsos(0).
Esta función se representa:
Caso: 3.
editarEsta función se representa:
Caso: 4.
editarEsta función se representa:
Estas funciones son equivalentes:
Caso: 5.
editarEsta función se representa:
Caso: 6.
editarEsta función se representa:
Estas funciones son equivalentes:
Caso: 7.
editarEsta función se representa:
Caso: 8.
editarEsta función se representa:
Caso: 9.
editarEsta función se representa:
Caso: 10.
editarEsta función se representa:
Caso: 11.
editarEsta función se representa:
Estas funciones son equivalentes:
Caso: 12.
editarEsta función se representa:
Caso: 13.
editarEsta función se representa:
Estas funciones son equivalentes:
Caso: 14.
editarEsta función se representa:
Caso: 15.
editarEsta función se representa:
Caso: 16.
editarEsta función se representa:
Estas funciones son equivalentes:
Véase también
editarEnlaces externos
editarBibliografía
editar- Valentín Labarta, José Luis (2012). Introducción a los circuitos eléctricos básicos. Editorial Donostiarra, S.A. p. 64. ISBN 978-84-7063-459-8.
- Bragós Bardia, Ramon (1999). Circuitos y dispositivos electrónicos (6 edición). Edicions de la UPC, S.L. p. 463. ISBN 978-84-8301-291-8.
- García Rodríguez, Alfonso (1974). Teoría de la conmutación. Ministerio de Educación. ISBN 84-369-0369-2.
Referencias
editar- ↑ Richard Johnsonbaugh (2005). «11». Matemática discreta (Marcia Aída González Osuna, trad.) (6 edición). Pearson Educación. p. 472. ISBN 978-97-02606-37-6.
- ↑ Lladonosa Giró, Vicente (1993). «1». Circuitos básicos de contactores y temporizadores. Marcombo. p. 9. ISBN 978-84-2670-916-5.