Coordenadas parabólicas
Las coordenadas parabólicas son un sistema de coordenadas ortogonales bidimensionales en el que las líneas de coordenadas son parábolas confocales.[1]
Una versión tridimensional de las coordenadas parabólicas, denominado coordenadas cilíndricas parabólicas, se obtiene mediante la rotación del sistema bidimensional sobre el eje de simetría de las parábolas.
Las coordenadas parabólicas poseen numerosas aplicaciones, como por ejemplo, el tratamiento del efecto Stark y la teoría del potencial.
Coordenadas parabólicas bidimensionales
editarLas coordenadas parabólicas bidimensionales para se definen por las ecuaciones:
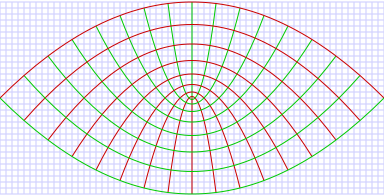
Las curvas con constante forman parábolas confocales
abiertas hacia arriba (en sentido ), mientras que las curvas con constante forman parábolas confocales
abiertas hacia abajo (en sentido ). Los focos de todas las parábolas se ubican en el origen.
Factores de escala bidimensionales
editarLos factores de escala de las coordenadas parabólicas equivalen a:
Para un elemento infinitesimal de área es
y su Laplaciano es:
Otros operadores diferenciales tales como y pueden expresarse para coordenadas (σ, τ) substituyendo los factores de escala en las fórmulas generales encontrados en las coordenadas ortogonales.
Coordenadas parabólicas tridimensionales
editarLas coordenadas parabólicas bidimensionales forman la base para dos conjuntos de coordenadas ortogonales tridimensionales. Las coordenadas cilíndricas parabólicas son producidas por proyección en la dirección .
La rotación sobre el eje de simetría de las parábolas produce un conjunto de paraboloides confocales, formando un sistema de coordenadas que también es conocido como "coordenadas parabólicas"
donde las parábolas están alineadas con el eje , sobre el cual se ha realizado la rotación. Así, el ángulo azimutal es definido por
Las superficies cuyo es constante forman paraboloides confocales
con concavidades hacia arriba (o sea, en sentido ), mientras que las superficies con constante forman paraboloides confocales
de concavidad hacia abajo (o sea, en sentido ). Los focos de todos estos paraboloides están localizados en el origen.
El tensor métrico de Riemann asociado a este sistema de coordenadas es
Factores de escala tridimensionales
editarLos tres factores de escala tridimensionales son:
Nótese que los factores de escala y son los mismos del caso bidimensional. El elemento infinitesimal de volumen es entonces
Y el laplaciano es dado por
Otros operadores diferenciales tales como y pueden ser expresados en coordenadas sustituyendo los factores de escala en las fórmulas generales encontradas en coordenadas ortogonales.
Fórmula alternativa
editarLa conversión de coordenadas cartesianas a parabólicas se realiza a través de la siguiente transformación:
El jacobiano de la transformación dada vincula términos infinitesimales como
siendo
- y
Si φ = 0 se obtiene una sección transversal con las coordenadas limitadas al plano xz:
Sea η=c (una constante), entonces
Esta es una parábola con foco en el origen, para cualquier valor c. Su eje de simetría es vertical y su concavidad está orientada hacia arriba.
Se ξ=c entonces
Esta es una parábola con foco en el origen, para cualquier valor de c. Su eje de simetría es vertical y su concavidad está orientada hacia abajo.
Ahora, considérese cualquier parábola η = c para arriba y toda parábola ξ = b hacia abajo. Si se desea encontrar su intersección:
entonces
y agrupando x²
se cancelan los factores comunes de ambos lados
tomando su raíz cuadrada,
x es la media geométrica de b y c. Una vez hallada la abscisa de la intersección, se procede a obtener la ordenada. Sustituyendo el valor de x en la ecuación de la parábola con la concavidad orientada hacia arriba:
y ahora, sustituyendo el valor de x en la ecuación de la parábola con la concavidad hacia abajo:
zc = zb. Por lo tanto, el punto de intersección es
Trácense ahora un par de tangentes a través del punto P, con una tangente en cada parábola. La recta tangente por el punto P a la parábola superior tiene la pendiente:
La recta tangente a través del punto P a la parábola inferior tiene la pendiente:
El producto de las dos pendientes es:
El producto de las pendientes es una "pendiente negativa" porque las rectas son perpendiculares. Esto es cierto para cualquier par de parábolas con las concavidades en direcciones opuestas.
Así mismo, un par de parábolas se cruzan en dos puntos, pero cuando φ es cero, en realidad limita las otras coordenadas ξ y η para moverse en el semiplano con x>0, ya que x<0 corresponde a φ = π.
Por lo tanto, un par de coordenadas ξ y η especifican un solo punto en el semiplano. Al variar φ entre 0 y 2π, el semiplano vuelve al punto (alrededor del eje z, que es el eje de revolución): la fórmula de los paraboloides. Un par de paraboloides opuestos se cortan en circunferencias, y el valor de φ especifica un semiplano que corta a través de la intersección con la circunferencia un solo punto. Las coordenadas cartesianas de los puntos son: [Menzel, p. 139]
Véase también
editarReferencias
editar- ↑ Dictionary of Analysis, Calculus, and Differential Equations. CRC Press. 1999. pp. 192 de 288. ISBN 9781420049992. Consultado el 21 de octubre de 2023.
Bibliografía
editar- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. pp. 660. ISBN 0-07-043316-X.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 185–186.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 180. ASIN B0000CKZX7.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 96.
- Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9. Mismo cuando Morse & Feshbach (1953), sustituyendo uk para ξk.
- Moon P, Spencer DE (1988). «Parabolic Coordinates (μ, ν, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print edición). New York: Springer-Verlag. pp. 34-36 (Table 1.08). ISBN 978-0-387-18430-2.
Enlaces externos
editar- Hazewinkel, Michiel, ed. (2001), "Hazewinkel, Michiel, ed. (2001), «Coordenadas parabólicas», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.", , ,
- MathWorld Descripción de coordenadas parabólicas