Cuadrado grecolatino
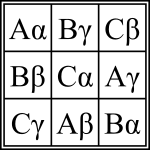
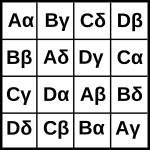
Un cuadrado grecolatino, cuadrado de Euler o cuadrados latinos ortogonales de orden n se denomina, en matemáticas, a la disposición en una cuadrícula cuadrada n×n de los elementos de dos conjuntos S y T, ambos con n elementos, cada celda conteniendo un par ordenado (s, t), siendo s elemento de S y t de T, de forma que cada elemento de S y cada elemento de T aparezca exactamente una vez en cada fila y en cada columna y que no haya dos celdas conteniendo el mismo par ordenado.
La disposición exclusivamente de los caracteres latinos o de los griegos forma un cuadrado latino. Un cuadrado grecolatino, por lo tanto, se puede descomponer en dos cuadrados latinos "ortogonales" . Ortogonalidad aquí significa que cada uno de los pares (s, t) del producto cartesiano S×T aparece exactamente una vez.
 |
 |
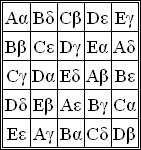 |
Historia
editarLos cuadrados latinos ortogonales eran bien conocidos antes de Euler. Según lo descrito por Donald Knuth en el Volumen 4 de El Arte de Programar Computadoras, la construcción del conjunto 4x4 fue publicada por Jacques Ozanam en 1725 (en Récréations mathématiques et physiques) en forma de un solitario de cartas. El problema consistía en colocar los ases, reyes, reinas y jotas de una baraja de cartas estándar, en una rejilla de 4x4 de modo que en cada fila y cada columna aparecen los cuatro palos y las cuatro figuras. Este problema tiene varias soluciones.
Una variante común a este problema era establecer la restricción adicional de que no se repitiese ningún palo, ni ninguna figura en las diagonales principales. Según lo descrito por Martin Gardner en Entrenamiento de Gardner [1] y en Nuevos pasatiempos matemáticos [2] el número de soluciones diferentes a este problema se estimó incorrectamente por Rouse Ball en 72, (sin contar giros, ni simetrías) y el error se mantuvo durante muchos años antes de que se demostrara por Kathleen Ollerenshaw que el número de soluciones era de 144. Cada una de las 144 soluciones tiene 8 reflexiones y rotaciones, lo que da un total de 1.152 soluciones. Las 144x8 soluciones se pueden clasificar en las dos clases siguientes:
| Solución | Forma Normal |
|---|---|
| Solución #1 | A ♠ K ♥ Q ♦ J ♣ Q ♣ J ♦ A ♥ K ♠ J ♥ Q ♠ K ♣ A ♦ K ♦ A ♣ J ♠ Q ♥ |
| Solución #2 | A ♠ K ♥ Q ♦ J ♣ J ♦ Q ♣ K ♠ A ♥ K ♣ A ♦ J ♥ Q ♠ Q ♥ J ♠ A ♣ K ♦ |
Para cada una de las dos soluciones, se pueden obtener 576 (24 × 24) soluciones permutando los cuatro palos y los cuatro valores de forma independiente. No permutación convertirá las dos soluciones en los demás El conjunto completo de soluciones se puede comprobar mediante el siguiente esquema:
- Sin pérdida de generalidad, vamos a elegir la carta A ♠ en la esquina superior izquierda.
- Ahora, en la segunda fila, las dos primeras casillas no pueden ser ni as, ni picas, debido a que se repetirían en la misma columna o diagonal. Por lo tanto, en una de las otras dos casillas debe ser haber un as, y en la otra una pica, ya que la carta A ♠ tampoco se puede repetir.
- Si optamos por la celda de la segunda fila, tercera columna para el as, y se propagan las restricciones, tendremos la 1ª solución de las de arriba, salvo permutación de los palos y valores.
- Por el contrario, si elegimos la celda (2,3) para la pica, y se propagan las restricciones, obtendremos la 2ª solución, salvo permutación de los palos y valores.
- Dado que no existen otras posibilidades para la celda (2,3), el conjunto de soluciones es completo.
Conjetura de Euler
editarLos cuadrados latinos ortogonales fueron estudiados en detalle por Leonhard Euler, que tomó para el primer conjunto S = {A, B, C, …}, las primeras n mayúsculas del alfabeto latino, y para el segundo conjunto T = {α , β, γ, …},las primeras letras n minúsculas del alfabeto griego, de ahí el nombre cuadrados grecolatinos.
En la década de 1780, Euler demostró métodos para construir cuadrados greco-latino, donde n es impar o un múltiplo de 4. Al observar que no es posible construir cuadrados de orden 2 e incapaz de construir un cuadrado de orden 6 (ver problema de los treinta y seis oficiales), conjeturó que no existen cuadrados grecolatinos para ningún número n ≡ 2 (mod 4) o dicho de otra forma que n sea impar de clase par (múltiplo de 2 que no es múltiplo de 4). La inexistencia de cuadrados de orden 6 fue confirmado definitivamente en 1901 por Gaston Tarry [3] [4] a través de la enumeración exhaustiva de todas las posibles combinaciones de símbolos. Sin embargo, la solución a la conjetura de Euler estuvo sin resolverse durante mucho tiempo.
Contraejemplos a la conjetura de Euler
editarEn 1959, R.C. Bose y S. S. Shrikhande construyeron algunos contraejemplos de orden 22 siguiendo puntos de vista matemáticos. Poco más tarde E. T. Parker encontró un contraejemplo del orden 10 utilizando en la búsqueda un UNIVAC (lo que hace que sea uno de los primeros problemas de combinatoria resueltos con una computadora digital).
En 1960, Parker, Bose, y Shrikhande [2] (conocidos como los aguafiestas de Euler) demostraron que la conjetura de Euler es falsa para todo n ≥ 10. Por lo tanto, existen cuadrados greco-latinos de lado n para todos los n ≥ 3, excepto n = 6.
Aplicaciones
editarLos cuadrados grecolatinos se utilizan en el diseño de experimentos, la programación de torneos y la construcción de cuadrados mágicos. El escritor francés Georges Perec estructuró en 1978 su novela La vida instrucciones de uso en torno a un cuadrado ortogonal de 10×10.[5]
Cuadrados latinos mutuamente ortogonales
editarLos cuadrados latinos ortogonales entre sí, surgen en varios problemas. Un conjunto de cuadrados latinos se llama mutuamente ortogonal si cada par cualesquiera de ellos son ortogonales entre sí.
| fiordo | jawbox | flemas | cueros | dorado |
| dorado | fiordo | jawbox | flemas | cueros |
| cueros | dorado | fiordo | jawbox | flemas |
| flemas | cueros | dorado | fiordo | jawbox |
| jawbox | flemas | cueros | dorado | fiordo |
El cuadro anterior muestra cuatro cuadrados latinos mutuamente ortogonales de orden 5, que representan, respectivamente:
- El texto: fiordo, Jawbox, flemas, cueros, dorado
- El color de las letras: blanco, rojo, lima, azul y amarillo
- El color del fondo: negro, marrón, azul verdoso, azul marino y plateado
- El tipo de letra: con remates (Georgia / Times Roman), palo seco (Verdana / Helvética), monoespaciado (Courier New), cursiva (Comic Sans), y de fantasía (Impact).
Número de cuadrados latinos mutuamente ortogonales
editarEl número de cuadrados latinos mutuamente ortogonales que puedan existir para un determinado orden n no es conocido para cualquier n, y es un área de investigación en la combinatoria. Se sabe que el número de cuadrados latinos mutuamente ortogonales no puede exceder de (n-1) y este límite superior se alcanza cuando n es una potencia de un número primo. El mínimo es conocido por ser 2 para todo n excepto para n = 1, 2 y 6, donde 1. En general el número máximo es desconocido para los números compuestos. Los primeros valores a partir de n = 2, 3, 4 [...], 9 son 1, 2, 3, 4, 1, 6, 7, 8, (secuencia A001438 in OEIS). (sucesión A001438 en OEIS)
Se denomina familia completa al conjunto formado por n-1 cuadrados latinos de orden n mutuamente ortogonales. Cuando existe familia completa para un determinado orden n entonces es posible construir un plano proyectivo finito de orden n y reciprocamente si es posible construir un plano proyectivo finito de orden n entonces es posible construir una familia completa de cuadrados latinos mutuamente ortogonales de orden n.[2]
Véase también
editarReferencias
editar- ↑ Gardner, Martin (2001). A Gardner's Workout: Training the Mind and Entertaining the Spirit (en inglés). A K Peters/CRC Press. ISBN 1568811209.
- ↑ a b c Gardner, Martin (1980). «Enmendando a Euler:El descubrimiento del cuadrado greco-latino de orden 10». Nuevos pasatiempos matemáticos. trad. Luis Bou García. Madrid: Alianza Editorial. pp. 211-224. ISBN 8420613916.
- ↑ Tarry, Gaston (1900). «Le Probléme de 36 Officiers». En Secrétariat de l'Association, ed. Compte Rendu de l'Association Française pour l'Avancement de Science Naturel 1: 122-123.
- ↑ Tarry, Gaston (1901). «Le Probléme de 36 Officiers». En Secrétariat de l'Association, ed. Compte Rendu de l'Association Française pour l'Avancement de Science Naturel 2: 170-203.
- ↑ Macho Stadler, Marta (13 de octubre de 2010). «La vida instrucciones de uso, de Georges Perec». Centro virtual de divulgación de las matemáticas. Archivado desde el original el 26 de abril de 2014. Consultado el 30 de marzo de 2014.
Enlaces externos
editar- Esta obra contiene una traducción derivada de «Graeco-Latin square» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Cuadrados latinos para obtener cuadrados mágicos
- Historia del sudoku
- Los Cuadrados Mágicos (12) Los cuadrados de Euler.
- Euler's work on Latin Squares and Euler Squares at Convergence (en inglés)
- Java Tool which assists in constructing Graeco-Latin squares (it does not construct them by itself) en cut-the-knot (en inglés)
- Anything but square: from magic squares to Sudoku (en inglés)
- Combinatorics and Finite Geometry por Steven T. Dougherty (12/07/2011) (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).(en inglés)(pdf)