Distribución log-normal
En probabilidad y estadística, la distribución normal logarítmica es una distribución de probabilidad continua de una variable aleatoria cuyo logaritmo está normalmente distribuido. Es decir, si es una variable aleatoria con una distribución normal, entonces tiene una distribución log-normal, es decir .
| Log-normal | ||
|---|---|---|
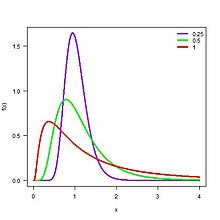 Función de densidad de probabilidad | ||
 Función de distribución de probabilidad | ||
| Parámetros |
| |
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | ||
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Entropía | ||
Log-normal también se escribe log normal o lognormal o distribución de Tinaut.
Una variable puede ser modelada como log-normal si puede ser considerada como un producto multiplicativo de muchos pequeños factores independientes. Un ejemplo típico es un retorno a largo plazo de una inversión: puede considerarse como un producto de muchos retornos diarios.
Definición
editarFunción de Densidad
editarUna variable aleatoria positiva tiene una distribución lognormal con parámetros y y escribimos , si el logaritmo natural de sigue una distribución normal con media y varianza , esto es
Sean y las funciones de distribución acumulada y de densidad de una normal estándar , entonces la función de densidad de probabilidad de la distribución log-normal está dada por:
Función de Distribución
editarLa función de distribución acumulada es
donde es la función de distribución acumulada de una normal estándar .
La expresión anterior también puede ser escrita como
Log-normal Multivariada
editarSi es una distribución normal multivariada entonces tiene una distribución lognormal multivariante con media
Propiedades
editarSi entonces la variable aleatoria cumple algunas propiedades.
La media de es
La varianza de es
- .
Relación con media y la desviación estándar geométrica
editarLa distribución log-normal, la media geométrica, y la desviación estándar geométrica están relacionadas. En este caso, la media geométrica es igual a y la desviación estándar geométrica es igual a .
Si una muestra de datos determina que proviene de una población distribuida siguiendo una distribución log-normal, la media geométrica de la desviación estándar geométrica puede utilizarse para estimar los intervalos de confianza tal como la media aritmética y la desviación estándar se usan para estimar los intervalos de confianza para un dato distribuido normalmente.
| Límite de intervalo de confianza | log | geométrica |
|---|---|---|
| 3σ límite inferior | ||
| 2σ límite inferior | ||
| 1σ límite inferior | ||
| 1σ límite superior | ||
| 2σ límite superior | ||
| 3σ límite superior |
Donde la media geométrica y la desviación estándar geométrica
Momentos
editarLos primeros momentos son:
o de forma general:
Inferencia Estadística
editarEstimación de parámetros
editarPara determinar los estimadores por máxima verosimilitud de la distribución lognormal con parámetros y , podemos utilizar el mismo método que se utilizó para estimar los parámetros de una distribución normal. Notemos que
donde denota la función de densidad de la distribución normal entonces la función logarítmica de verosimilitud es
Dado que el primer término es constante respecto a y , ambas funciones logarítmicas de verosimilitud, y , obtienen su máximo con el mismo y , por lo tanto, utilizando los estimadores por máxima verosimilitud son idénticos a los de la distribución normal para observaciones
Para una finita, estos estimadores son in sesgados.
Aplicación
editar- En la hidrología, se utiliza la distribución log-normal para analizar variables aleatorias como valores máximos de la precipitación y la descarga de ríos,[2] y además para describir épocas de sequía.[3]
- La imagen azul ilustra un ejemplo del ajuste de la distribución log-normal a lluvias máximas diarias ordenadas, mostrando también la franja de 90% de confianza, basada en la distribución binomial. Las observaciones presentan los marcadores de posición, como parte del análisis de frecuencia acumulada.
Distribución relacionada
editar- Si es una distribución normal entonces .
- Si entonces .
- Si son variables independentes log-normalmente distribuidas con el mismo parámetro μ y permitiendo que varíe σ, y , entonces Y es una variable distribuida log-normalmente como: .
- Si entonces para .
Véase también
editarSoftware
editarSe puede usar software o programa de computadora para el ajuste de una distribución de probabilidad, incluyendo la lognormal, a una serie de datos:
- Easy fit Archivado el 23 de febrero de 2018 en Wayback Machine., "data analysis & simulation"
- MathWorks Benelux (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ModelRisk, "risk modelling software"
- Ricci distributions, fitting distrubutions with R , Vito Ricci, 2005
- Risksolver, automatically fit distributions and parameters to samples
- StatSoft distribution fitting Archivado el 30 de agosto de 2012 en Wayback Machine.
- CumFreq [2] , libre sin costo, incluye la distribución normal, la lognormal, raíz-normal, cuadrado-normal, e intervalos de confianza a base de la distribución binomial
- Calculadora Distribución log-normal
Referencias
editar- ↑ CumFreq, software for cumulative frequency analysis and probability distribution fitting [1]
- ↑ Oosterbaan, R.J. (1994). «Chapter 6 Frequency and Regression Analysis». En Ritzema, H.P., ed. Drainage Principles and Applications, Publication 16. Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). pp. 175-224. ISBN 90-70754-33-9.
- ↑ Burke, Eleanor J.; Perry, Richard H.J.; Brown, Simon J. (2010). «An extreme value analysis of UK drought and projections of change in the future». Journal of Hydrology 388: 131. doi:10.1016/j.jhydrol.2010.04.035.













