Distribución t no central

En Teoría de la probabilidad y Estadística, la distribución t no central generaliza la distribución t de Student mediante un parámetro de no centralidad. Así como en un contraste de hipótesis de igualdad de medias en una población normal, la distribución t de Student describe el estadístico de contraste cuando la hipótesis nula es cierta (igualdad de medias), la distribución t no central lo hace cuando la hipótesis nula es falsa; en consecuencia, es especialmente importante en el cálculo de la potencia estadística de un contraste. También se utiliza en la modelización robusta de datos.

Distribución t no central
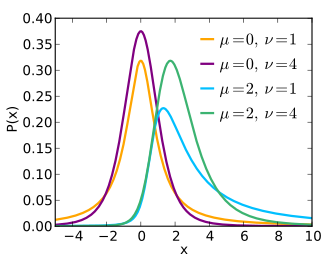Función de densidad de probabilidad
Parámetros	ν > 0 grados de libertad $\mu \in \mathbb {R}$ parámetro de no centralidad
Dominio	$x\in (-\infty ;+\infty )\,\!$
Función de densidad (pdf)	Ver texto
Función de distribución (cdf)	Ver texto
Media	$\mu \,{\sqrt {\dfrac {\nu }{2}}}\,{\dfrac {\Gamma {\Big (}{\frac {\nu -1}{2}}{\Big )}}{\Gamma {\Big (}{\frac {\nu }{2}}{\Big )}}},$ si $\nu >1.$
Varianza	${\dfrac {\nu (1+\mu ^{2})}{\nu -2}}-{\dfrac {\mu ^{2}\nu }{2}}\left({\dfrac {\Gamma {\Big (}{\frac {\nu -1}{2}}{\Big )}}{\Gamma {\Big (}{\frac {\nu }{2}}{\Big )}}}\right)^{2}$, si $\nu >2.$

Definición

Sea $Z$ una variable aleatoria normal estándar ${\mathcal {N}}(0,1)$ y $V\sim \chi _{\nu }^{2}$ una variable aleatoria χ² con $\nu >0$ grados de libertad que es independiente de $Z$. Se dice​ que la variable aleatoria

$$T={\frac {Z+\mu }{\sqrt {V/\nu }}}$$

tiene una distribución t no central con $\nu >0$ grados de libertad y parámetro de no centralidad $\mu \in \mathbb {R}$ ; se escribe $T\sim t_{\nu }(\mu )$. Cuando $\mu =0$ se obtiene una distribución $t$ de Student ordinaria $t_{\nu }$. Debe tenerse en cuenta que el parámetro de no centralidad puede ser negativo.

Comentario sobre los grados de libertad no enteros. El caso habitual de esta distribución es cuando el número de grados de libertad $\nu$ es un número natural, pero tanto desde el punto de vista de las aplicaciones como de la teoría, es conveniente que esta distribución pueda tener cualquier número estrictamente positivo de grados de libertad, $\nu >0$. Esto es correcto gracias a que una distribución χ² cuadrado está bien definida para $\nu >0$.

Función de densidad

La función de densidad de la distribución t no central no tiene una expresión sencilla y veremos diversas formulaciones que aparecen en la literatura. Sea $T\sim t_{\nu }(\mu )$.

Expresión integral ​ $$f(t)={\frac {\nu ^{\nu /2}\,e^{-{\frac {\mu ^{2}\nu }{2(\nu +t^{2})}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma ({\frac {\nu }{2}})\,(\nu +t^{2})^{\frac {\nu +1}{2}}}}\int _{0}^{\infty }z^{\nu }e^{-{\frac {1}{2}}{\Big (}z-{\frac {t\mu }{\sqrt {\nu +t^{2}}}}{\Big )}^{2}}\,dz,\quad t\in \mathbb {R} .\qquad \qquad (1)$$ Es interesante observar que cuando $\nu$ es un número natural, esta fórmula puede escribirse en términos de la función $Hh$ ​ $$f(t)={\frac {\nu ^{\nu /2}\,\nu !\,e^{-{\frac {\mu ^{2}\nu }{2(\nu +t^{2})}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma ({\frac {\nu }{2}})\,(\nu +t^{2})^{\frac {\nu +1}{2}}}}\,Hh_{\nu }{\Big (}-{\frac {t\mu }{\sqrt {\nu +t^{2}}}}{\Big )},\quad t\in \mathbb {R} ,$$ donde $$Hh_{n}(x)={\frac {1}{n!}}\int _{0}^{\infty }z^{n}e^{-{\frac {1}{2}}(z+x)^{2}}\,dz={\frac {1}{n!}}\int _{x}^{\infty }(u-x)^{n}e^{-{\frac {1}{2}}u^{2}}\,du.$$ Sobre la función $Hh$ consultar, por ejemplo, Jeffreys and Jeffreys. ​

Expresión en serie. ​ $$f(t)={\frac {\nu ^{\nu /2}\,e^{-\mu ^{2}/2}}{{\sqrt {\pi }}\,\Gamma ({\frac {\nu }{2}})}}\sum _{j=0}^{\infty }{\frac {\mu ^{j}}{j!}}\,2^{j/2}\Gamma (\nu +j+1){\frac {t^{j}}{(t^{2}+\nu )^{\frac {\nu +j+1}{2}}}},\quad t\in \mathbb {R} .\qquad \qquad (2)$$

Expresión mediante funciones especiales.

Utilizando la función cilíndrica parabólica $U$​(ver la versión digital ​),

tenemos que ​$$f(t)={\frac {{\sqrt {2}}{\big (}{\frac {\nu }{2}}{\big )}^{\frac {\nu }{2}}\,\Gamma (\nu +1)}{{\sqrt {\pi }}\,\Gamma ({\frac {\nu }{2}})}}{\frac {e^{-{\frac {\mu ^{2}}{4(\nu +t^{2})}}(2\nu +t^{2})}}{(\nu +t^{2})^{\frac {\nu +1}{2}}}}\,U{\Big (}\nu +{\frac {1}{2}},-{\frac {t\mu }{\sqrt {\nu +t^{2}}}}{\Big )},\quad t\in \mathbb {R} .\qquad \qquad (3)$$ Mediante la función hipergeométrica confluente o función de Kummer $_{1}\!F_{1}(a;b;z)$ , también denotada por $M(a,b,z)$ ​, $$f(t)=\underbrace {{\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}{\Big (}1+{\frac {t^{2}}{\nu }}{\Big )}^{-{\tfrac {\nu +1}{2}}}} _{{\text{Densidad de la }}t{\text{ de Student ordinaria}}}e^{-\mu ^{2}/2}{\Big \{}A_{\nu }(t,\mu )+B_{\nu }(t,\mu ){\Big \}},\qquad \qquad (4)$$donde $${\begin{aligned}A_{\nu }(t,\mu )&={_{1}\!F}_{1}\left({\frac {\nu +1}{2}}\,;\,{\frac {1}{2}}\,;\,{\frac {\mu ^{2}t^{2}}{2(t^{2}+\nu )}}\right),\\B_{\nu }(t,\mu )&={\frac {{\sqrt {2}}\mu t}{\sqrt {t^{2}+\nu }}}{\frac {\Gamma ({\frac {\nu }{2}}+1)}{\Gamma ({\frac {\nu +1}{2}})}}{_{1}\!F}_{1}\left({\frac {\nu }{2}}+1\,;\,{\frac {3}{2}}\,;\,{\frac {\mu ^{2}t^{2}}{2(t^{2}+\nu )}}\right),\end{aligned}}$$

Expresión en términos de la función de distribución El software estadístico R y otros programas estadísticos utilizan la siguiente expresión para calcular la función de densidad [1]:

$$f(t)={\begin{cases}{\dfrac {\nu }{t}}\,{\Bigg (}F_{\nu +2,\mu }\left(t{\sqrt {1+{\frac {2}{\nu }}}}\right)-F_{\nu ,\mu }(t){\Bigg )},&{\mbox{si}}\ t\neq 0,\\\\{\dfrac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\pi \nu }}\,\Gamma ({\frac {\nu }{2}})}}\,e^{-\mu ^{2}/2},&{\mbox{si}}\ t=0,\end{cases}}\qquad \qquad (5)$$donde $F_{\nu ,\mu }$ es la función de distribución de la distribución $t$ no central con $\nu$ grados de libertad y parámetro de no centralidad $\mu$ (véase el siguiente apartado).

Demostraciones

Fórmula (1) Escribimos $$T={\frac {X}{Y}},$$donde $X\sim {\mathcal {N}}(\mu ,1)$, $Y=H/{\sqrt {\nu }}$, con $H\sim \chi _{\nu }$ (distribución χ con $\nu$ grados de libertad), $X$ y $Y$ independientes. Utilizando que si una variable aleatoria $M$ tiene función de densidad $f_{M}$, entonces la variable aleatoria $N=CM$, con $C\neq 0$, tiene función de densidad $f_{N}(x)={\frac {1}{\vert C\vert }}f{\big (}{\frac {x}{C}}{\big )}$, tenemos que la función de densidad de $Y$ es $$f_{Y}(y)={\frac {\nu ^{\frac {\nu }{2}}}{2^{{\frac {\nu }{2}}-1}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,y^{\nu -1}e^{-{\frac {\nu y^{2}}{2}}},\ y>0.$$Dada la independencia entre $X$ y $Y$, la función de densidad conjunta del vector $(X,Y)$ es $$f_{(X,Y)}(x,y)={\frac {\nu ^{\frac {\nu }{2}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,y^{\nu -1}e^{-{\frac {(x-\mu )^{2}+\nu y^{2}}{2}}},\quad (x,y)\in \mathbb {R} \times (0,\infty ).$$Consideremos la transformación $$h(X,Y)=(T,Y),\ {\text{con}}\ T={\frac {X}{Y}},$$ específicamente $${\begin{aligned}h:\mathbb {R} \times &(0,\infty )\rightarrow \mathbb {R} \times (0,\infty )\\&(x,y)\longmapsto (t,y)\end{aligned}}$$donde $t=x/y$. Esta función es biyectiva de clase $C^{1}$. La función inversa es $${\begin{aligned}g=h^{-1}:\mathbb {R} \times &(0,\infty )\rightarrow \mathbb {R} \times (0,\infty )\\&(t,y)\longmapsto (x,y)\end{aligned}}$$con $x=ty$. El valor absoluto del determinante jacobiano de $g$ es $J_{g}=y$. Por tanto la densidad de $(T,Y)$ (después de arreglar la expresión) es $$f_{(T,Y)}(t,y)={\frac {\nu ^{\frac {\nu }{2}}e^{-{\frac {\mu ^{2}}{2}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,y^{\nu }e^{-{\frac {(t^{2}+\nu )y^{2}-2ty\mu }{2}}},\quad (t,y)\in \mathbb {R} \times (0,\infty ).$$Entonces, para $t\in \mathbb {R}$, $$f_{T}(t)=\int _{0}^{\infty }f_{(T,Y)}(t,y)\,dy={\frac {\nu ^{\frac {\nu }{2}}e^{-{\frac {\mu ^{2}}{2}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,\int _{0}^{\infty }y^{\nu }e^{-{\frac {(t^{2}+\nu )y^{2}-2ty\mu }{2}}}\,dy.\quad \quad (*)$$Haciendo el cambio $z={\sqrt {\nu +t^{2}}}$, llegamos a la expresión (1) $$f(t)={\frac {\nu ^{\nu /2}\,e^{-{\frac {\mu ^{2}\nu }{2(\nu +t^{2})}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma (\nu /2)(\nu +t^{2})^{\frac {\nu +1}{2}}}}\int _{0}^{\infty }z^{\nu }e^{-{\frac {1}{2}}{\Big (}z-{\frac {t\mu }{\sqrt {\nu +t^{2}}}}{\Big )}^{2}}\,dz.$$ Expresión en serie. Volvamos a la expresión (*), que equivale a $$f_{T}(t)={\frac {\nu ^{\frac {\nu }{2}}e^{-{\frac {\mu ^{2}}{2}}}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,\int _{0}^{\infty }y^{\nu }e^{-{\frac {(t^{2}+\nu )y^{2}}{2}}}\,e^{-ty\mu }\,dy,$$y descompongamos $e^{ty\mu }$ en serie de potencias en la variable $y$. A continuación se razona que puede intercambiarse la integral con el sumatorio y se llega a $$f_{T}(t)={\frac {\nu ^{\frac {\nu }{2}}e^{-{\frac {\mu ^{2}}{2}}}t^{j}\mu ^{j}}{{\sqrt {\pi }}\,2^{\frac {\nu -1}{2}}\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}j!}}\sum _{j=0}^{\infty }\int _{0}^{\infty }y^{\nu +j}e^{-{\frac {(t^{2}+\nu )y^{2}}{2}}}\,dy.$$Ahora se calcula cada integral mediante el cambio de variable $(t^{2}+\nu )y^{2}/2=z$ , con lo que obtenemos (2). Expresiones en términos de funciones especiales. La fórmula (3) se deduce de la fórmula (1) utilizando la representación integral de la función cilíndrica parabólica $U$ ​: para $a>-1/2$, $$U(a,t)={\frac {e^{-t^{2}/4}}{\Gamma ({\frac {1}{2}}+a)}}\int _{0}^{\infty }z^{a-{\frac {1}{2}}}e^{-{\frac {z^{2}}{2}}-zt}\,dz.$$ La fórmula (4) se obtiene a partir de (3) mediante la relación entre las funciones cilíndricas parabólicas y las funciones hipergeométricas confluentes ​ ​ ​ $$U(a,x)={\frac {\sqrt {\pi }}{2^{{\frac {a}{2}}+{\frac {1}{4}}}\,\Gamma ({\frac {3}{4}}+{\frac {a}{2}})}}\,e^{-x^{2}/4}\,_{1}\!F_{1}{\Big (}{\frac {a}{2}}+{\frac {1}{4}};{\frac {1}{2}};{\frac {x^{2}}{2}}{\Big )}-{\frac {\sqrt {\pi }}{2^{{\frac {a}{2}}-{\frac {1}{4}}}\,\Gamma ({\frac {1}{4}}+{\frac {a}{2}})}}\,x\,e^{-x^{2}/4}\,_{1}\!F_{1}{\Big (}{\frac {a}{2}}+{\frac {3}{4}};{\frac {3}{2}};{\frac {x^{2}}{2}}{\Big )}.$$Expresión en términos de la función de distribución (5): véase el siguiente apartado..

Función de distribución

La función de distribución de la distribución t no central con $\nu$ grados de libertad y parámetro de no centralidad $\mu$ se puede expresar como ​​ $$F_{\nu ,\mu }(x)={\begin{cases}{\widetilde {F}}_{\nu ,\mu }(x),&{\mbox{si }}x\geq 0,\\\\1-{\widetilde {F}}_{\nu ,-\mu }(-x),&{\mbox{si }}x<0,\end{cases}}\qquad \qquad (6)$$donde $${\widetilde {F}}_{\nu ,\mu }(x)=\Phi (-\mu )+{\frac {1}{2}}\sum _{j=0}^{\infty }{\bigg (}p_{j}I_{y}{\Big (}j+{\frac {1}{2}},{\frac {\nu }{2}}{\Big )}+q_{j}I_{y}{\Big (}j+1,{\frac {\nu }{2}}{\Big )}{\bigg )},\qquad \qquad (7)$$

$I_{y}\,\!(a,b)$ es la función beta incompleta regularizada,

$$y={\frac {x^{2}}{x^{2}+\nu }},\quad p_{j}={\frac {1}{j!}}\,{\bigg (}{\frac {\mu ^{2}}{2}}{\bigg )}^{j}\,e^{-\mu ^{2}/2}\quad {\text{y}}\quad q_{j}={\frac {\mu }{{\sqrt {2}}\,\Gamma (j+{\frac {3}{2}})}}\,{\bigg (}{\frac {\mu ^{2}}{2}}{\bigg )}^{j}\,e^{-\mu ^{2}/2},$$

y $\Phi$ es la función de distribución de la distribución normal estándar. Nótese que ${\widetilde {F}}_{\nu ,\mu }(x)$ sólo depende de $x^{2}$ y por tanto en (6), para $x<0$ es indistinto poner ${\widetilde {F}}_{\nu ,-\mu }(-x)$ o ${\widetilde {F}}_{\nu ,-\mu }(x)$.

Demostración

Esta fórmula se deduce a partir de la expresión en serie de la función de densidad (2). Empezaremos demostrando una fórmula intermedia que nos será de utilidad más adelante. Argumentando que la convergencia de la serie en (2) es uniforme en cualquier intervalo finito ​ , podemos integrar término a cabo; concretamente, para $x>0$, se obtiene $$P(0<T\leq x)=\int _{0}^{x}f(t)\,dt={\frac {1}{2{\sqrt {\pi }}}}\sum _{j=0}^{\infty }{\frac {\mu ^{j}}{j!}}2^{j/2}\,\Gamma {\Big (}{\frac {j+1}{2}}{\Big )}I_{x^{2}/(\nu +x^{2})}{\Big (}{\frac {j+1}{2}},{\frac {\nu }{2}}{\Big )}.$$Ahora se utiliza la fórmula de duplicación de la función gamma: $$\Gamma {\Big (}{\frac {j+1}{2}}{\Big )}={\frac {2^{-j}j!\,{\sqrt {\pi }}}{\Gamma {\Big (}{\frac {j}{2}}+1{\Big )}}},$$y se obtiene $$P(0<T\leq x)={\frac {1}{2}}\,e^{-\mu ^{2}/2}\sum _{j=0}^{\infty }{\frac {\mu ^{j}}{2^{j/2}}}\,{\frac {1}{\Gamma {\Big (}{\frac {j}{2}}+1{\Big )}}}I_{x^{2}/(\nu +x^{2})}{\Big (}{\frac {j+1}{2}},{\frac {\nu }{2}}{\Big )}.$$ Por otro lado, $$P(T\leq 0)=P{\Big (}{\frac {Z+\mu }{\sqrt {V/\nu }}}\leq 0{\Big )}=P(Z+\mu \leq 0)=P(Z\leq -\mu )=\Phi (-\mu ).$$Así, $$F_{\nu ,\mu }(x)=P(T\leq 0)+P(0<T\leq x)=\Phi (-\mu )+{\frac {1}{2}}\,e^{-\mu ^{2}/2}\sum _{j=0}^{\infty }{\frac {\mu ^{j}}{2^{j/2}}}\,{\frac {1}{\Gamma {\Big (}{\frac {j}{2}}+1{\Big )}}}I_{x^{2}/(\nu +x^{2})}{\Big (}{\frac {j+1}{2}},{\frac {\nu }{2}}{\Big )}.\qquad \qquad (8)$$Designemos la expresión de la derecha por ${\widetilde {F}}_{\nu ,\mu }(x)$ . Para $x\leq 0$ , tenemos$${\begin{aligned}P(T\leq x)&=P{\Big (}{\frac {Z+\mu }{\sqrt {V/\nu }}}\leq x{\Big )}=P{\Big (}{\frac {Z}{\sqrt {V/\nu }}}\leq x-{\frac {\mu }{\sqrt {V/\nu }}}{\Big )}=P{\Big (}{\frac {Z}{\sqrt {V/\nu }}}\geq -x+{\frac {\mu }{\sqrt {V/\nu }}}{\Big )}\\&=1-P{\Big (}{\frac {Z-\mu }{\sqrt {V/\nu }}}\leq -x{\Big )}=1-{\widetilde {F}}_{\nu ,-\mu }(-x)=1-{\widetilde {F}}_{\nu ,-\mu }(x),\end{aligned}}$$donde hemos utilizado que $Z/{\sqrt {V/\nu }}$ es simétrica respecto al 0 y que la función ${\widetilde {F}}_{\nu ,\mu }(x)$ que hemos calculado antes sólo depende de $x^{2}$ . Finalmente, para obtener la expresión (7), el sumatorio de (8) se separa en dos, uno para los índices $j$ pares y el otro para los impares.

Demostración de la fórmula de la densidad en términos de la función de distribución

La demostración consiste en calcular la diferencia $F_{\nu +2,\mu }{\bigg (}t{\sqrt {1+{\frac {2}{\nu }}}}{\bigg )}-F_{\nu ,\mu }(t)$ utilizando la fórmula (8). Fijemos $t>0$; el punto clave de la prueba es que en la expresión (8) de $F_{\nu +2,\mu }{\bigg (}t{\sqrt {1+{\frac {2}{\nu }}}}{\bigg )}$ y de $F_{\nu ,\mu }(t)$, para cada término $j$ del sumatorio, el subíndice de la función gamma incompleta es el mismo . Concretamente, si definimos la función$$y(z,\alpha )={\frac {z^{2}}{\alpha +z^{2}}},$$entonces, $$y{\Big (}t{\sqrt {1+{\tfrac {2}{\nu }}}},\nu +2{\Big )}=y(t,\nu )={\frac {t^{2}}{\nu +t^{2}}}.$$A a partir de esa observación se aplica la fórmula ​ $$I_{y}(p,q+1)-I_{y}(p,q)={\frac {y^{p}(1-y)^{q}}{q\,B(p,q)}},$$donde $B(p,q)$ es la función Beta, en cada una de las diferencias entre los sumandos del mismo índice $j$ (ambas series son convergentes y las podemos restar término a término), de donde $$I_{\frac {t^{2}}{\nu +t^{2}}}{\Big (}{\frac {j+1}{2}},{\frac {\nu +2}{2}}{\Big )}-I_{\frac {t^{2}}{\nu +t^{2}}}{\Big (}{\frac {j+1}{2}},{\frac {\nu }{2}}{\Big )}={\frac {{\Big (}{\frac {t^{2}}{\nu +t^{2}}}{\Big )}^{\frac {j+1}{2}}{\Big (}1-{\frac {t^{2}}{\nu +t^{2}}}{\Big )}^{\frac {\nu }{2}}\,\Gamma ({\frac {\nu +j+1}{2}})}{{\frac {\nu }{2}}\,\Gamma ({\frac {j+1}{2}})\,\Gamma ({\frac {\nu }{2}})}}.$$ Aplicando la fórmula de duplicación de la función beta y simplificando, juntando todos los términos del sumatorio, se obtiene $t/\nu$ que multiplica la expresión de la derecha de (2), con lo que se demuestra (5 ) cuando $t>0$. Para $t<0$ , por los cálculos efectuados, tenemos que$$F_{\nu +2,\mu }{\bigg (}t{\sqrt {1+{\frac {2}{\nu }}}}{\bigg )}-F_{\nu ,\mu }(t)={\widetilde {F}}_{\nu ,-\mu }(-t)-{\widetilde {F}}_{\nu +2,-\mu }{\bigg (}-t{\sqrt {1+{\frac {2}{\nu }}}}{\bigg )}={\frac {-t}{\nu }}{\big (}-f_{\nu ,-\mu }(-t){\big )},$$donde $f_{\nu ,\mu }(t)$ designa la función de densidad de la distribución $t$ con $\nu$ grados de libertad y parámetro de no centralidad $\mu$. Pero como se comprueba a partir de (1) o (2), $$f_{\nu ,-\mu }(-t)=f_{\nu ,\mu }(t).$$

Momentos

El momento de orden $k$ de una distribución $t$ no central es ​

$${\mbox{E}}\left[T^{k}\right]={\begin{cases}{\Big (}{\dfrac {\nu }{2}}{\Big )}^{\frac {k}{2}}\,{\dfrac {\Gamma {\big (}{\frac {\nu -k}{2}}{\big )}}{\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}\,e^{-\mu ^{2}/2}{\dfrac {d^{k}e^{\mu ^{2}/2}}{d\mu ^{k}}},&{\mbox{si }}k<\nu ,\\\\{\mbox{no existe}},&{\mbox{si }}k\geq \nu ,\end{cases}}$$

donde $d^{k}e^{\mu ^{2}/2}/d\mu ^{k}$ designa la derivada de orden k -ésimo de la función $e^{\mu ^{2}/2}$ .

En particular, la media y la varianza son: $${\begin{aligned}{\mbox{E}}[T]&={\begin{cases}\mu \,{\sqrt {\dfrac {\nu }{2}}}\,{\dfrac {\Gamma {\Big (}{\frac {\nu -1}{2}}{\Big )}}{\Gamma {\Big (}{\frac {\nu }{2}}{\Big )}}},&{\mbox{si }}\nu >1,\\\\{\mbox{no existe}},&{\mbox{si }}\nu \leq 1,\\\end{cases}}\\\\{\mbox{Var}}(T)&={\begin{cases}{\dfrac {\nu (1+\mu ^{2})}{\nu -2}}-{\dfrac {\mu ^{2}\nu }{2}}\left({\dfrac {\Gamma {\Big (}{\frac {\nu -1}{2}}{\Big )}}{\Gamma {\Big (}{\frac {\nu }{2}}{\Big )}}}\right)^{2},&{\mbox{si }}\nu >2,\\\\{\mbox{no existe}},&{\mbox{si }}\nu \leq 2.\\\end{cases}}\end{aligned}}$$

Demostración

Debido a la independencia entre el numerador i el denominador en la definición de la distribución $t$ no central, a que una variable normal tiene momentos de todos los órdenes y que $V\geq 0$, el cálculo de los momentos se reduce a $$E[T^{k}]=\nu ^{k/2}E{\big [}V^{-k/2}{\big ]}\,E{\big [}(Z+\mu )^{k}{\big ]},$$ pudiendo ser esta expresión finita o $+\infty$. Por un lado, para la distribución normal estándar $Z\sim {\mathcal {N}}(0,1)$ tenemos la siguiente expresión: $$E{\big [}(Z+\mu )^{k}{\big ]}=e^{-\mu ^{2}/2}\,{\dfrac {d^{k}e^{\mu ^{2}/2}}{d\mu ^{k}}}.$$ Por otra parte, debido a que $V\geq 0$, podemos calcular la siguiente integral para cualquier número natural $k$ $$E{\big [}V^{-k/2}{\big ]}={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{-k/2}x^{(\nu /2)-1}e^{-x/2}\,dx={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{(\nu -k)/2-1}e^{-x/2}\,dx.$$ Hacemos el cambio de variables $y=x/2$, y la integral de la derecha da $2^{(\nu -n)/2}\Gamma ((\nu -k)/2)$ $(\nu -k)/2>0$, y $+\infty$ en caso contrario.

Aplicación al cálculo de la potencia del contraste t de Student

Véase Johnson and Welch ​. Sea $X_{1},\dots ,X_{n}$ una muestra de una población normal ${\mathcal {N}}(\mu ,\sigma ^{2})$, es decir, las variables aleatorias $X_{1},\dots ,X_{n}$ son independientes y todas tienen distribución ${\mathcal {N}}(\mu ,\sigma ^{2})$. Fijado un número $\mu _{0}\in \mathbb {R}$. Queremos contrastar $$H_{0}:\ \mu =\mu _{0}\qquad {\text{contra}}\quad H_{1}:\ \mu >\mu _{0}.$$ En el contraste de Student, el estadístico de contraste es $$T={\frac {{\overline {X}}-\mu _{0}}{S/{\sqrt {n}}}},$$ donde ${\overline {X}}$ és la media muestral y $S^{2}$ es la varianza muestral (modificada): $${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}\quad {\text{y}}\quad S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2}.$$ Bajo la hipótesis nula $H_{0}$, $T\sim t_{n-1}$ (véase la distribución $t$ de Student). Fijado un nivel de significación $\alpha \in (0,1)$ (habitualmente $\alpha =0'05$ o $0'01$), para determinar la región crítica calculamos el valor $c_{\alpha }$ tal que$$P(W>c_{\alpha })=\alpha ,$$donde $W\sim t_{n-1}$ En este contexto, rechazamos $H_{0}$ si $T>c_{\alpha }$. Dado un valor $\mu _{1}>\mu _{0}$ (por tanto, de la hipótesis alternativa), podemos calcular la potencia del test, es decir, la probabilidad de rechazar la hipótesis nula cuando es falsa, en este punto, de la siguiente manera: escribimos$$T={\frac {{\overline {X}}-\mu _{0}}{S/{\sqrt {n}}}}={\frac {{\frac {{\overline {X}}-\mu _{1}}{\sigma /{\sqrt {n}}}}+{\frac {\mu _{1}-\mu _{0}}{\sigma /{\sqrt {n}}}}}{S/\sigma }}.$$En la expresión de la derecha,

1. Si suponemos $\mu =\mu _{1}$, entonces $({\overline {X}}-\mu _{1})/(\sigma /{\sqrt {n}})\sim {\mathcal {N}}(0,1)$ .
2. Tenemos que $${\frac {S^{2}}{\sigma ^{2}}}={\frac {(n-1)S^{2}}{(n-1)\sigma ^{2}}}={\frac {{\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})}{n-1}},$$y por tanto $S^{2}/\sigma ^{2}$ es una variable aleatoria con una distribución $\chi _{n-1}^{2}$ (véase la distribución χ²) dividida por sus grados de libertad.
3. Las variables aleatorias de los puntos 1 y 2 son independientes (véase la distribución χ²) .

En consecuencia, si $\mu =\mu _{1}$, tenemos que $T\sim t_{n-1}{\bigg (}{\frac {\mu _{1}-\mu _{0}}{\sigma /{\sqrt {n}}}}{\bigg )}$. Por tanto, la potencia del test en el punto $\mu _{1}$ será $$P(T>c_{\alpha }\,\vert \mu =\mu _{1})=1-F_{n-1,{\frac {\mu _{1}-\mu _{0}}{\sigma /{\sqrt {n}}}}}(c_{\alpha }).$$

Uso en intervalos de tolerancia

Los intervalos de tolerancia normales unilaterales tienen una solución exacta en términos de la media muestral y la varianza muestral basada en la distribución t no central ​. Esto permite calcular un intervalo estadístico dentro del cual, con cierto nivel de confianza, se encuentra una proporción especificada de la población.

Referencias

• Datos: Q6960434