Espectroscopía rotacional
La espectroscopía rotacional es un tipo de espectroscopía que se dedica a la medición de las energías de transición entre estados rotacionales cuantizados de moléculas en fase gaseosa. La energía rotacional de moléculas polares puede medirse como absorción o emisión de microondas[1] o mediante espectroscopía infrarroja lejana. el espectro rotacional de moléculas no polares no puede observarse por estos métodos pero puede medirse a través de la espectroscopía Raman. La espectroscopía rotacional a veces es nombrada "pura", para distinguirla de la espectroscopía rotacional-vibracional, donde los cambios en la energía rotacional están sobrepuestos con los cambios en la energía vibracional. También sirve para distinguirla de la espectroscopía ro-vibrónica, donde los cambios de energía rotacional, vibracional y electrónica están sobrepuestos.
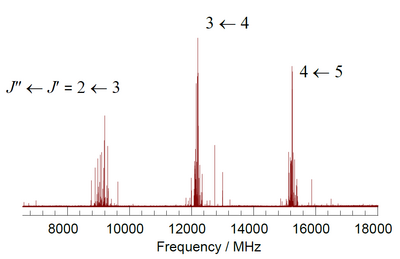
3I. Cada transición rotacional está marcada con el número cuántico J del estado inicial y final , y están altamente desdobladas debido a los efectos del acoplamiento cuadrupolar nuclear con el núcleo de 127I.
Para la espectroscopía rotacional, las moléculas se clasifican de acuerdo a su simetría en esféricas, lineales y altamente simétricas. Es posible derivar expresiones analíticas para los términos de la energía rotacional de estas moléculas. Las expresiones analíticas pueden derivarse para una cuarta categoría: las moléculas asimétricas, para niveles rotacionales hasta J=3, sin embargo, niveles superiores deben determinarse a través de métodos numéricos. Las energías rotacionales se derivan teóricamente considerando a las moléculas como rotores rígidos y luego aplicando términos correctivos para la distorsión centrífuga, la estructura fina, la estructura hiperfina y el acoplamiento de Coriolis. El ajuste de las expresiones teóricas a los espectros experimentales arroja valores numéricos del momento angular de inercia de los cuales se derivan valores precisos de longitudes y ángulos de enlace. En presencia de un campo electrostático, el desdoblamiento de Stark permite determinar los momentos dipolares eléctricos.
Una aplicación importante de la espectroscopía rotacional es la exploración de la composición química del medio interestelar a través de radiotelescopios.
Aplicaciones
editarLa espectroscopía rotacional ha sido utilizada principalmente para investigar aspectos fundamentales de física molecular. Es una herramienta única para la determinación de estructuras moleculares en fase gas. Puede utilizarse para establecer barreras de rotación interna como la asociada a la rotación del metilo (CH3) en relación con el grupo clorobenceno (C6H4Cl) en el clorotolueno (C7H7Cl).[2] Cuando la estructura fina e hiperfina son observables, la técnica también provee información acerca de las estructuras electrónicas de las moléculas. Una buena parte del entendimiento de las interacciones moleculares débiles como las de van der Waals, puentes de hidrógeno y puentes de halógeno se han establecido a través de esta técnica.
En relación con la radioastronomía, la técnica posee un papel esencial en la exploración de la composición química del medio interestelar. Las transiciones de microondas se miden en el laboratorio y luego se comparan con las emisiones del medio interestelar medidas con un radiotelescopio. El amoniaco (NH3) fue la primera molécula poliatómica estable en ser identificada en el medio interestelar.[3] Por otro lado, la medición del monóxido de cloro es relevante para la química atmosférica, pues se sabe que la reducción en los niveles de ozono está relacionada con la activación de compuestos halogenados, especialmente el antes mencionado.[4] Los proyectos actuales en la radioastronomía involucran tanto la espectroscopía de microondas en laboratorio y las observaciones de radiotelescopios modernos como el ALMA.[5]
Generalidades
editarUna molécula en fase gas es libre de rotar en relación con un conjunto de ejes ortogonales de orientación fija en el espacio, centrados en el centro de masa de la molécula. La rotación libre no es posible en fase gaseosa o sólida debido a la presencia de interacciones intermoleculares. La rotación alrededor de cada eje está asociada con un conjunto de niveles de energía cuantizados dependientes del momento de inercia de ese eje y de un número cuántico. Por lo tanto, para moléculas lineales, los niveles energéticos se describen con un único momento de inercia y un único número cuántico J, que define la magnitud del momento angular rotacional.
Para moléculas no lineales que son rotores simétricos, existen dos momentos de inercia y cuya energía depende también de un segundo número cuántico rotacional K, que define el componente vectorial del momento angular rotacional alrededor del principal eje de simetría.[6] El análisis de datos espectroscópicos con las expresiones detalladas más abajo resulta en la determinación cuantitativa de los valores de momento de inercia. De estos valores de la estructura molecular, se pueden obtener sus dimensiones.
Para una molécula lineal, el análisis del espectro rotacional provee valores para la constante rotacional y el momento de inercia de la molécula. Conociendo las masas atómicas, puede utilizarse para determinar la longitud de enlace directamente. Para moléculas diatómicas, este proceso es directo. Para moléculas lineales con más de dos átomos, es necesario medir el espectro de dos o más isotopólogos, como 16O12C32S contra 16O12C34S. Esto permite que un conjunto de ecuaciones simultáneas se agrupen y resuelvan para las longitudes de enlace. El valor obtenido por este método puede diferir de la longitud de enlace al equilibrio, debido a que existe energía de punto cero en el estado vibracional basal, al cual, el estado rotacional está referido, mientras que la longitud de enlace al equilibrio se encuentra en el mínimo de la curva de energía potencial. La relación entre las constantes rotacionales está dada por la ecuación:
donde v es el número cuántico vibracional y alfa es una constante de interacción vibracional-rotacional que puede ser calculada si se tienen los valores de B para dos diferentes estados vibracionales.[7]
Para otras moléculas, si el espectro puede ser resuelto y se pueden asignar transiciones individuales, se pueden deducir las longitudes y ángulos de enlace. Cuando esto no es posible, como sucede con las moléculas asimétricas, lo único que se puede hacer es ajustar el espectro a 3 momentos de inercia calculados para una estructura molecular asumida. Al variar la estructura molecular, el ajuste puede mejorarse, dando una estimación cualitativa de su estructura. La sustitución isotópica es invaluable al utilizar esta aproximación para la determinación de la estructura molecular
Clasificaciones de los rotores moleculares
editarEn mecánica cuántica, la rotación libre de una molécula se encuentra cuantizada, por lo que la energía rotacional y el momento angular pueden obtener únicamente valores fijos, los cuales están relacionados con el momento de inercia de la molécula. Para cualquier estructura, existen tres momentos de inercia: que se encuentran tres ejes ortogonales A, B y C, con origen en el centro de masa del sistema. La convención general es definir los ejes de manera que con el eje A correspondiendo al menor momento de inercia. Algunos autores, sin embargo, definen el eje A como el eje de rotación molecular de mayor orden.
El patrón particular de niveles de energía (y, por lo tanto, las transiciones del espectro rotacional) para una molécula está determinada por su simetría. Una manera conveniente de verlo es dividirlas en 4 clases, basándonos en la simetría de su estructura. Estos son:
Rotor esférico
editarLos tres momentos de inercia son iguales entre sí . Ejemplos de estos incluyen el fósforo elemental (P4), tetracloruro de carbono (CCl4) y otros tetra haluros, metano (CH4), silano (SiH4), hexafluoruro de azufre (SF6) y otros hexa haluros. Estas moléculas pertenecen a los grupos puntuales Td u Oh.
Moléculas lineales
editarLos momentos de inercia se ordenan de forma que . Para la mayoría de los propósitos, se puede aproximar . Ejemplos de estos son el oxígeno (O2), nitrógeno (N2), monóxido de carbono (CO), el radical hidroxilo (HO•), dióxido de carbono (CO2), cianuro de hidrógeno (HCN), sulfuro de carbonilo (SCO), acetileno (HCCH) y dihaloetinos. Estas moléculas pertenecen a los grupos puntuales C∞v o D∞h.
Rotores simétricos
editarUn rotor simétrico es una molécula en la que dos de sus momentos de inercia son los mismos y el tercero no es despreciable, aunque sí es menor, de forma que o . Por definición, un rotor simétrico debe tener un eje de rotación de orden 3 o superior. Por conveniencia, los espectroscopistas dividen las moléculas en 2 clases: rotores simétricos oblatos (en forma de disco), donde y rotores simétricos prolatos (balón de fútbol americano), donde . El espectro es completamente diferente e instantáneamente reconocible. Ejemplos incluyen:
- Oblatos: benceno (C6H6), amoniaco (NH3), tetrafluoruro de xenón (XeF4)
- Prolatos: clorometano (CH3Cl), propino (CH3CCH)
Rotores asimétricos
editarUn rotor asimétrico es aquel en el que los tres momentos de inercia poseen valores diferentes. Ejemplos de moléculas pequeñas asimétricas incluyen el agua (H2O) y el dióxido de nitrógeno (NO2), cuyos ejes de mayor orden son de 2. La mayoría de las moléculas grandes son asimétricas.
Reglas de selección
editarMicroondas e infrarrojo lejano
editarLas transiciones entre estados rotacionales pueden observarse en moléculas con un momento dipolar eléctrico permanente.[8] Una consecuencia de esta regla es que no pueden observarse espectros de microondas para moléculas centrosimétricas lineales como nitrógeno o etino, los cuales son no polares. Las moléculas tetraédricas como el metano, que poseen un momento dipolar nulo y una polarizabilidad isotrópica, no tendrían un espectro de rotación puro, sin embargo, debido al efecto de la distorsión centrífuga, cuando la molécula rota alrededor de un eje de simetría de orden 3, se crea un pequeño momento dipolar, permitiendo observar un espectro débil de rotación en la espectroscopía de microondas.[8]
En moléculas simétricas, la regla de selección para las transiciones de moléculas con dipolo permanente (y por lo tanto, permitidas por la primera regla) es que . Debido a que estas transiciones se deben a la absorción o emisión de un único fotón con espín 1, la conservación del momento angular implica que el cambio en el momento angular puede ser sólo de una unidad.[6] Más allá de eso, el número cuántico K está limitado a valores entre +J y -J.[7]
Referencias
editar- ↑ Cook, Robert L. (1984). Microwave molecular spectra (3rd ed edición). Wiley. ISBN 978-0-471-08681-9. OCLC 11090587. Consultado el 10 de septiembre de 2021.
- ↑ «Millimeterwave rotational spectrum and internal rotation in o-chlorotoluene». Journal of Molecular Spectroscopy (en inglés) 237 (2): 137-142. 1 de junio de 2006. ISSN 0022-2852. doi:10.1016/j.jms.2006.03.011. Consultado el 10 de septiembre de 2021.
- ↑ Cheung, A. C.; Rank, D. M.; Townes, C. H.; Thornton, D. D.; Welch, W. J. (16 de diciembre de 1968). «Detection of N${\mathrm{H}}_{3}$ Molecules in the Interstellar Medium by Their Microwave Emission». Physical Review Letters 21 (25): 1701-1705. doi:10.1103/PhysRevLett.21.1701. Consultado el 10 de septiembre de 2021.
- ↑ Ricaud, P.; Baron, P.; de La Noë, J. (14 de junio de 2004). «Quality assessment of ground-based microwave measurements of chlorine monoxide, ozone, and nitrogen dioxide from the NDSC radiometer at the Plateau de Bure». Annales Geophysicae (en inglés) 22 (6): 1903-1915. ISSN 0992-7689. doi:10.5194/angeo-22-1903-2004. Consultado el 10 de septiembre de 2021.
- ↑ «Astrochemistry | Department of Astronomy, U.Va.». astronomy.as.virginia.edu. Consultado el 10 de septiembre de 2021.
- ↑ a b De Paula, Julio (2006). Atkins' Physical chemistry (8th ed edición). Oxford University Press. ISBN 978-0-19-870072-2. OCLC 62307289. Consultado el 10 de septiembre de 2021.
- ↑ a b McCash, Elaine M. (1994). Fundamentals of molecular spectroscopy (4th ed edición). McGraw-Hill. ISBN 0-07-707976-0. OCLC 29753560. Consultado el 17 de septiembre de 2021.
- ↑ a b Hollas, J. Michael (1996). Modern spectroscopy (3rd ed edición). J. Wiley. ISBN 0-471-96522-7. OCLC 34192026. Consultado el 17 de septiembre de 2021.