Evolvente

La evolvente del círculo, a veces llamada involuta, es una curva plana de desarrollo, cuyas normales son tangentes de la circunferencia.

Evolvente del círculo.

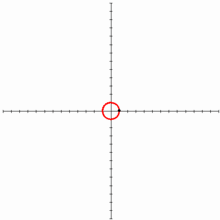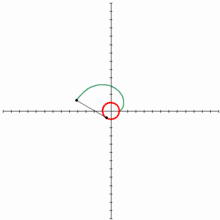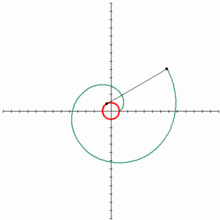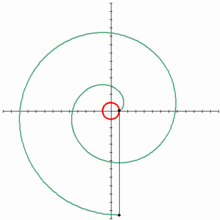
A menudo se traza sin saberlo: cuando un hilo tenso o un cable se desenrollan de una bobina circular sus puntos describen la evolvente de la circunferencia de esa bobina.

Fue estudiada originalmente por Christian Huygens,​ que trataba de diseñar relojes de péndulo para uso marino. Huygens utilizó la cicloide para forzar la oscilación regular del péndulo. Cuando un hilo tenso se enrolla en una cicloide cada uno de sus puntos describe un cicloide, es decir, la curva de desarrollo de una cicloide es una cicloide, como la de una circunferencia es una evolvente. La aplicación a los perfiles de las ruedas dentadas fue propuesta por Leonhard Euler.​

Definición matemática

La evolvente de la circunferencia (en trazo negro) es semejante a la Espiral de Arquímedes (en rojo), pero no coinciden.

La curva se puede definir paramétricamente mediante la siguiente ecuación:

${\begin{cases}x(t)=k(\cos {t}+t\,\operatorname {sen} {t})\\y(t)=k(\operatorname {sen} {t}-t\,\cos {t})\end{cases}}$

donde k es el radio en el punto de contacto.

También puede ser definido por una ecuación intrínseca:

$R_{c}^{2}=2k\,s$, donde $R_{c}$ representa el radio de curvatura y la $s$ la abscisa curvilínea.

Propiedades y aplicaciones

Si se hace rodar sin deslizamiento una recta sobre un círculo, cada punto de esta línea describe con respecto al círculo una evolvente.

Engranajes con perfil en evolvente.

Los dientes de los engranajes rectos tienen perfil de evolvente de circunferencia, porque garantiza una relación de transmisión constante y una transmisión de energía óptima entre los engranajes, ya que en el punto de contacto entre dos dientes la tangente al perfil es común a ambos dientes.

Otras propiedades notables de engranajes de evolvente son las siguientes:

1. Si un diente de engranaje de perfil de evolvente engrana con otro diente con el mismo perfil, a velocidad de rotación uniforme, el movimiento angular de la rueda accionada es uniforme también, incluso cuando variamos la distancia entre ejes.
2. La velocidad de movimiento relativo entre la rueda conductora y la rueda conducida de un engranaje está establecida por los diámetros de sus círculos base.
3. El contacto de acoplamiento entre el diente de las ruedas conducida y conductora se producen a lo largo de una recta tangente al círculo base de las ruedas. Esta recta se llama línea de acción. Pasa en general entre los círculos base (engranajes convencional), pero puede estar fuera (en el llamado engranaje paradójico, cuyas ruedas giran en el mismo sentido). A lo largo de esta recta están los puntos de engrane, en los que el deslizamiento relativo entre las superficies es cero.
4. Las superficies de desgaste activo se distribuye de manera más uniforme.
5. Las vibraciones son más bajas que con otro perfil.

La longitud de la evolvente es equivalente a $d\cdot \pi ^{2}\cdot \theta ^{2}$, donde:

• d es el diámetro del círculo
• π es el número pi
• θ es el ángulo en revoluciones

Véase también

• Clotoide
• Desarrollo (geometría)
• Engranaje
• Espiral
• Christiaan Huygens
• Leonhard Euler

Enlaces externos

• Curvas Técnicas y Cíclicas por José Antonio Cuadrado (15/5/12)
• Weisstein, Eric W. «Evolvente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q680712
• Multimedia: Involute / Q680712