Pentágono
En geometría, se denomina pentágono (del griego πεντάγωνον, de πέντε pénte "cinco" y γωνία gōnía "ángulo") a un polígono de cinco lados y cinco vértices. La suma de los ángulos internos de un simple pentágono es 540°.
| Pentágono | ||
|---|---|---|
 Un pentágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 5 | |
| Vértices | 5 | |
| Grupo de simetría | , orden 2x5 | |
| Símbolo de Schläfli | {5} (pentágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
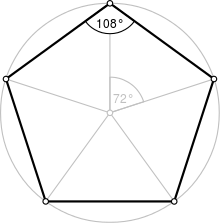
| Ángulo interior | 108° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Un pentágono puede ser simple o auto-intersecantes. Un pentágono regular auto-intersecante (o pentágono estrella ) se llama Estrella pentagonal
Definición
editarUn pentágono regular es aquel que tiene todos sus lados iguales y sus ángulos internos congruentes.
Proposiciones
editar- Cada ángulo interno mide 108 grados o radianes.
- Es convexo.
- Cada ángulo externo del pentágono regular mide 72°.
- Tiene exactamente cinco diagonales.
- Un pentágono regular se puede inscribir como circunscribir en sendas circunferencias circuncéntricas.
- Las dos diagonales que parten de un vértice común determinan en el pentágono tres triángulos en sucesión, uno en la parte media : isósceles, cuyos lados iguales son las diagonales; dos triángulos iguales a los costados del anterior, son también isósceles por tener como lados iguales, dos de los lados del pentágono regular.
- Lo interesante es que las dos diagonales trisecan al ángulo de cuyo vértice parten, pues cada ángulo mide 36°, cuya suma da el ángulo en el vértice de 108° .
Propiedades
editarApotema
editarLa apotema, , de un pentágono regular de lado es[1]
Área
editarEl área de un pentágono regular de lado es
O, en función el radio de la circunferencia circunscrita, ,
O bien,
Y en función de la apotema, [1]
Perímetro
editarEl perímetro de un pentágono regular lado es
O bien, en función de la apotema ( ),[1]
Fórmula para calcular los ángulos interiores
editarLa suma de los ángulos internos de un pentágono es de 540°.
La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es:
El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5):
Movimientos
editar- El pentágono regular es una figura simétrica respecto del eje que contiene un apotema y su prolongación que pasa por el vértice opuesto a la base del apotema.
- Hay cinco ejes de simetría
- Cinco casos de rotación: la de 72°, 144°, 216°,288° y 360°[2]
Construcción de un pentágono regular
editarUn pentágono regular es construible usando un compás y una regla, ya sea inscribiendo uno en un círculo dado o construyendo uno en un lado dado. Euclides describió este proceso en sus Elementos, alrededor del año 300 a. C.[3][4]
Se puede construir con regla y compás un pentágono regular, inscrito en una circunferencia (véase la figura), de la siguiente manera:
- Trazamos dos rectas perpendiculares (aunque de la segunda solo nos interesa un segmento, OQ en la figura) por el centro O de la circunferencia (PD y OQ en la figura). Determinamos el punto medio M del segmento OQ y trazamos la recta PM. Con centro en M, trazamos la circunferencia de radio MO. Denotemos con R y S las intersecciones de esta circunferencia con la recta PM. Las circunferencias de centro en P y radios PR y PS determinan los vértices del pentágono regular.
Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él. En el centro quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.
Método de Richmond
editarUn método para construir un pentágono regular en un círculo dado es el descrito por Richmond[5] y discutido con más detalle en Polyhedra de Cromwell.[6]
El panel superior muestra la construcción utilizada en el método de Richmond para crear el lado del pentágono inscrito. El círculo que define el pentágono tiene radio unitario. Su centro está situado en el punto C y un punto medio M está marcado en la mitad de su radio. Este punto se une a la periferia verticalmente por encima del centro en el punto D. El ángulo CMD es bisecado, y la bisectriz interseca el eje vertical en el punto Q. Una recta horizontal que pasa por Q corta al círculo en el punto P, y la cuerda PD es el lado necesario del pentágono inscrito.
Para determinar la longitud de este lado, se representan debajo del círculo los dos triángulos rectángulos DCM y QCM. Utilizando el teorema de Pitágoras y dos lados, se halla la hipotenusa del triángulo mayor como . El lado h del triángulo menor se halla entonces utilizando la fórmula del semiángulo:
donde coseno y seno de ϕ del triángulo mayor son conocidos. El resultado es:
Si DP es realmente el lado de un pentágono regular, , por lo que DP = 2 cos(54°), QD = DP cos(54°) = 2cos2(54°), y CQ = 1 - 2cos2(54°), que es igual a -cos(108°) por la fórmula del doble ángulo del coseno. Este es el coseno de 72°, que es igual a como se desea.
Círculos de Carlyle
editarEl círculo de Carlyle se inventó como método geométrico para hallar las raíces de una ecuación cuadrática.[7] Esta metodología conduce a un procedimiento para construir un pentágono regular. Los pasos son los siguientes:[8]
- Dibuja un círculo en el que inscribir el pentágono y marca el punto central O.
- Traza una línea horizontal por el centro del círculo. Marca la intersección izquierda con el círculo como punto B.
- Traza una línea vertical que pase por el centro. Marca una intersección con el círculo como punto A.
- Construye el punto M como el punto medio de O y B.
- Dibuja un círculo centrado en M que pase por el punto A. Marca su intersección con la línea horizontal dentro del círculo original como el punto W y su intersección fuera del círculo como el punto V.
- Dibuja un círculo de radio OA y centro W. Corta al círculo original en dos de los vértices del pentágono.
- Dibuja un círculo de radio OA y centro V. Corta al círculo original en dos de los vértices del pentágono.
- El quinto vértice es la intersección más a la derecha de la recta horizontal con el círculo original.
Los pasos 6-8 son equivalentes a la siguiente versión, mostrada en la animación:
- 6a. Construye el punto F como punto medio de O y W.
- 7a. Construye una recta vertical que pase por F. Ésta interseca al círculo original en dos de los vértices del pentágono. El tercer vértice es la intersección más a la derecha de la recta horizontal con la circunferencia original.
- 8a. Construye los otros dos vértices utilizando el compás y la longitud del vértice hallada en el paso 7a.
Pentágonos equiláteros
editarUn pentágono equilátero es un polígono con cinco lados de igual longitud. Sin embargo, sus cinco ángulos internos pueden tomar una serie de valores, lo que le permite formar una familia de pentágonos. En cambio, el pentágono regular es único hasta la semejanza, porque es equilátero y es equiangular (sus cinco ángulos son iguales).
Pentágonos cíclicos
editarUn cíclico pentágono es aquel en el que una circunferencia, llamada circunscrita, pasa por los cinco vértices. El pentágono regular es un ejemplo de pentágono cíclico. El área de un pentágono cíclico, regular o no, puede expresarse como la cuarta parte de la raíz cuadrada de una de las raíces de una ecuación séptica cuyos coeficientes son funciones de los lados del pentágono.[9][10][11]
Existen pentágonos cíclicos con lados racionales y área racional, llamados pentágonos de Robbins. Se ha demostrado que las diagonales de un pentágono de Robbins deben ser todas racionales o todas irracionales, y se conjetura que todas las diagonales deben ser racionales.[12]
Pentágonos convexos generales
editarPara todos los pentágonos convexos, la suma de los cuadrados de las diagonales es menor que 3 veces la suma de los cuadrados de los lados.[13]: p.75, #1854
Pentágonos en mosaicos
editarUn pentágono regular no puede aparecer en ningún mosaico de polígonos regulares. En primer lugar, para demostrar que un pentágono no puede formar un teselado regular (uno en el que todas las caras son congruentes, lo que requiere que todos los polígonos sean pentágonos), observe que 360° / 108° = 31⁄3 (donde 108° es el ángulo interior), que no es un número entero; por tanto, no existe un número entero de pentágonos que compartan un único vértice y no dejen huecos entre ellos. Más difícil es demostrar que un pentágono no puede estar en ningún mosaico de borde a borde formado por polígonos regulares:
La máxima densidad de empaquetamiento conocida de un pentágono regular es de aproximadamente 0,921, lograda por el doble enrejado de empaquetamiento mostrado. En un preprint publicado en 2016, Thomas Hales y Wöden Kusner anunciaron una prueba de que el empaquetamiento de doble celosía del pentágono regular (al que llaman empaquetamiento "pentagonal ice-ray", y que remontan al trabajo de artesanos chinos en 1900) tiene la densidad óptima entre todos los empaquetamientos de pentágonos regulares en el plano.[14], su prueba aún no ha sido arbitrada y publicada.
No existen combinaciones de polígonos regulares con 4 o más vértices que contengan un pentágono. Para combinaciones con 3, si 3 polígonos se encuentran en un vértice y uno tiene un número impar de lados, los otros 2 deben ser congruentes. La razón de esto es que los polígonos que tocan las aristas del pentágono deben alternarse alrededor del pentágono, lo que es imposible debido al número impar de lados del pentágono. Para el pentágono, esto resulta en un polígono cuyos ángulos son todos (360 - 108) / 2 = 126°. Para encontrar el número de lados de este polígono tiene, el resultado es 360 / (180 - 126) = 62⁄3, que no es un número entero. Por lo tanto, un pentágono no puede aparecer en ningún mosaico formado por polígonos regulares.
Hay 15 clases de pentágonos que pueden alicatar monohedralmente el plano. Ninguno de los pentágonos tiene simetría en general, aunque algunos tienen casos especiales con simetría especular.
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
Relaciones geométricas del pentágono regular
editarRelación con el número áureo
editarVeamos que la razón entre un segmento que una dos de sus vértices no consecutivos y uno de los lados del pentágono es la razón aúrea o número áureo, por ejemplo que
Por simetría, los segmentos CE y CA son iguales. Observamos que los triángulos ANF y CMF son semejantes. De la semejanza de sus lados tenemos que
Observemos que MC es la mitad de CE y que AN es la mitad de AB. Por otra parte, como el triángulo FCD es isósceles, tenemos que FC = CD. Así podemos escribir AF = AC - FC = CE - CD. Por tanto
Sustituyendo CE/CD por tenemos
en otras palabras . Esta ecuación describe la razón dorada. es el único número positivo que cuando le restamos la unidad, obtenemos su inverso.
Algunas consideraciones sobre triángulos
editarConsideremos a un pentágono (regular) y la circunferencia circunscrita a dicho pentágono. Tracemos la perpendicular por el centro de la circunferencia al lado DA del pentágono y sea M la intersección de esta perpendicular con la circunferencia el ángulo AOB mide 360°/5=72° y el ángulo AOM es su mitad, es decir 36°. El ángulo MOB, suma de estos dos vale 108° y como el triángulo AOB es isósceles tenemos que
- La razón entre el segmento MB y el radio OM de la circunferencia es la razón dorada
Así, sea P la intersección de las rectas OA y MB. El triángulo PMO es isósceles, y la razón entre el radio OM y el segmento PM es la razón dorada. Finalmente, el triángulo OBP también es isósceles, con lo que PB = OB ( =OM). Tenemos :
Lo anterior se puede interpretar como una demostración geométrica de la ecuación (1).
Véase también
editarReferencias
editar- ↑ a b c Sapiña, R. «Calculadora del área y perímetro del pentágono regular». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 19 de junio de 2020.
- ↑ Tema análogo en Álgebra moderna de Birkhoff y Mac Lane.
- ↑ George Edward Martin (1998). Springer, ed. Construcciones geométricas (en inglés). p. 6. ISBN 0-387-98276-0.
- ↑ Euklid's Elements of Geometry, Book 4, Proposition 11 (Richard Fitzpatrick, trad.) (en inglés). 2008. p. 119. ISBN 978-0-6151-7984-1.
- ↑ Richmond, Herbert W. (1893). «A Construction for a Regular Polygon of Seventeen Sides». The Quarterly Journal of Pure and Applied Mathematics 26: 206-207.
- ↑ Peter R. Cromwell (22 de julio de 1999). Polyhedra. p. 63. ISBN 0-521-66405-5. Parámetro desconocido
|title-link=ignorado (ayuda) - ↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd edición). CRC Press. p. 329. ISBN 1-58488-347-2.
- ↑ DeTemple, Duane W. (Feb 1991). «Carlyle circles and Lemoine simplicity of polygon constructions». The American Mathematical Monthly 98 (2): 97-108. JSTOR 2323939. doi:10.2307/2323939. Archivado desde el original el 21 de diciembre de 2015.
- ↑ Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [1]
- ↑ Robbins, D. P. (1994). «Areas of Polygons Inscribed in a Circle». Discrete and Computational Geometry 12 (2): 223-236. doi:10.1007/bf02574377.
- ↑ Robbins, D. P. (1995). «Areas of Polygons Inscribed in a Circle». The American Mathematical Monthly 102 (6): 523-530. JSTOR 2974766. doi:10.2307/2974766.
- ↑ *Buchholz, Ralph H.; MacDougall, James A. (2008), «Cyclic polygons with rational sides and area», Journal of Number Theory 128 (1): 17-48, MR 2382768, doi:10.1016/j.jnt.2007.05.005..
- ↑ Desigualdades propuestas en "Crux Mathematicorum", [2].
- ↑ Hales, Thomas; Kusner, Wöden (September 2016), Empaquetamientos de pentágonos regulares en el plano, arXiv:1602.07220.
Enlaces externos
editar- Wikimedia Commons alberga una categoría multimedia sobre pentágonos.
- Wikcionario tiene definiciones y otra información sobre pentágono.
- Una posibilidad de poder ver pentágonos exactos mediante SVG se puede encontrar en Wikimedia Commons


