Pirámide pentagonal giroelongada
En geometría, la pirámide pentagonal giroelongada es uno de los sólidos de Johnson (J11). Como sugiere su nombre, se puede construir tomando una pirámide pentagonal y "giroelongándola", lo que supone pegar un antiprisma pentagonal a su base. También puede verse como un icosaedro con la tapa (una pirámide pentagonal, J2) cortada por un plano.
| Pirámide pentagonal giroelongada | ||
|---|---|---|
 Imagen del sólido | ||
| Tipo |
Johnson J10 - J11 - J12 | |
| Caras |
3x5 triángulos 1 pentágono | |
| Aristas | 25 | |
| Vértices | 11 | |
| Configuración de vértices |
5(33.5) 1+5(35) | |
| Grupo de simetría | C5v | |
| Poliedro dual | - | |
| Propiedades | ||
| Convexo | ||
| Desarrollo | ||
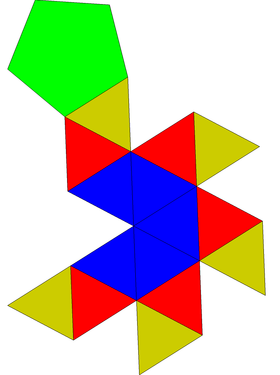 | ||
Un sólido de Johnson es uno de los 92 poliedros convexos que se componen estrictamente de caras poligonales regulares, pero que no son poliedros uniformes (es decir, no son sólidos platónicos, sólidos arquimedianos, prismas o antiprismas). Fueron nombrados por Norman Johnson, quien los enumeró por primera vez en 1966.[1]
También puede verse como un icosaedro disminuido, un icosaedro con la parte superior (un pirámide pentagonal, J2) cortada por un plano. Se pueden formar otros sólidos de Johnson cortando múltiples pirámides pentagonales de un icosaedro: el antiprisma pentagonal y el icosaedro metabidisminuido (eliminando dos pirámides) y el icosaedro tridisminuido (eliminando tres pirámides).
Poliedro dual
editarEl dual de la pirámide pentagonal giroelongada tiene 11 caras: 5 deltoides, 1 pentágono regular y 5 pentágonos irregulares.
| Poliedro dual de la pirámide pentagonal giroelongada | Desarrollo del dual |
|---|---|
Referencias
editar- ↑ Johnson, Norman W. (1966), «Convex polyhedra with regular faces», Canadian Journal of Mathematics 18: 169-200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8..
Enlaces externos
editar- Weisstein, Eric W. «Johnson solid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Gyroelongated pentagonal pyramid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.