Plano de Fano

En geometría proyectiva, el plano de Fano (cuyo nombre se debe a Gino Fano) es el plano proyectivo finito con el menor número posible de puntos y líneas: solo 7 de cada uno.

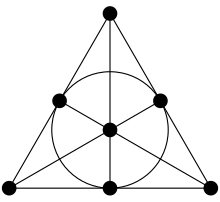
Definiciones formales

Coordenadas homogéneas

Está construido sobre el espacio vectorial $Z_{2}^{3}$ y sus siete puntos pueden representarse como coordenadas homogéneas utilizando una codificación binaria de números distintos de cero, de la siguiente manera:

(0,0,1)

(0,1,0)

(1,0,0)

(0,1,1)

(1,0,1)

(1,1,0)

(1,1,1)

Definición axiomática

Otra manera de definir el plano de Fano es mediante los siguientes axiomas:

Cada línea del plano tiene al menos tres puntos.
Por cada punto del plano pasan al menos tres líneas.
Por cada par de puntos pasa una y solo una línea.
Cada par de líneas se une exactamente en un punto.
Cada línea del plano tiene un máximo de tres puntos.
Por cada punto del plano pasan a lo más tres líneas.

Los dos últimos axiomas son los que realmente determinan un plano de Fano.

Matriz de incidencia

Sea A={1,2,3,4,5,6,7} el conjunto de vértices que conforman el Plano de Fano, entonces este también puede representarse como el hipergrafo conformado por las hiperaristas {1,2,3}, {1,4,7}, {1,5,6}, {2,4,5}, {2,6,7}, {3,4,6} y {3,5,7}. Una tercera manera de definir el Plano de Fano es, entonces, a través de la matriz de incidencia de este hipergrafo. Es decir, como la matriz booleana:

1 2 3 4 5 6 7
1 1 1 0 0 0 0 1 0 0 1 0 0 1 1 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0 1 1 0 1 0 0 0 1 0 1 0 1

Referencias

Baez, John (2002), «The Octonions», Bull. Amer. Math. Soc. 39: 145-205, doi:10.1090/S0273-0979-01-00934-X .. Online HTML version at http://math.ucr.edu/home/baez/octonions/.
van Lint, J.H.; Wilson, R.M. (1992), A Course in Combinatorics, Cambridge University Press, p. 197 ..
Manivel, L. (2006), «Configurations of lines and models of Lie algebras», Journal of Algebra 304 (1): 457-486, doi:10.1016/j.jalgebra.2006.04.029 ..
Weisstein, Eric W. «Fano Plane». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Finite plane and Fano plane en PlanetMath.

Véase también

Datos: Q1395814
Multimedia: Fano plane / Q1395814