Poliedro noble
Un poliedro noble se caracteriza por ser isoedral (tener todas las caras iguales) e isogonal (todos los vértices iguales).[1] Fueron estudiados por primera vez en profundidad por Hess y Bruckner a finales del siglo XIX, y más tarde por Grünbaum.[2]
 | |
 disfenoide |
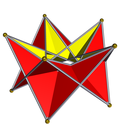 pentagonal |
Clases de poliedros nobles
editarHay cuatro clases principales de poliedros nobles:
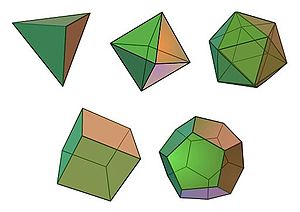
- [1] Los nueve poliedros regulares también son nobles.
- [2] Tetraedros disfenoides, que junto con los sólidos platónicos son los únicos poliedros convexos nobles.
- [3] Poliedros en corona o estefanoides, toda una serie infinita de toroides.
- Distintos ejemplos variados, dado que no se sabe si su número es finito o no, y cuántos pueden quedar por ser descubiertos.
Si se consideran como poliedros algunas de las construcciones extrañas de Grünbaum, entonces se incluirían dos series infinitas más de toroides:
- Poliedros en guirnalda. Poseen caras triangulares en pares coplanares que comparten un borde.
- Poliedros con caras en V. Poseen vértices en pares coincidentes y caras degeneradas.
Dualidad de los poliedros nobles
editarSe puede distinguir entre formas estructurales duales (topologías) por un lado, y disposiciones geométricas duales cuando se intercambian alrededor de una esfera concéntrica por el otro. En lo que sigue, el término 'dual' cubre ambos tipos cuando no se indica lo contrario.
El dual de un poliedro noble también es noble. Muchos también son autoduales:
- Los nueve poliedros regulares forman pares duales, siendo el tetraedro auto dual.
- Los tetraedros disfenoides son todos topológicamente idénticos. Geométricamente vienen en pares duales: uno alargado y otro correspondientemente aplastado.
- Un poliedro en corona es topológicamente auto dual. No se sabe si existen ejemplos geométricamente autoduales.
- Los poliedros en guirnalda y los poliedros con caras en V son duales entre sí.
Referencias
editar- ↑ Mircea Vasile Diudea (2017). Multi-shell Polyhedral Clusters. Springer. pp. 40 de 442. ISBN 9783319641232. Consultado el 24 de noviembre de 2019.
- ↑ Polytopes: Abstract, Convex and Computational. Springer Science & Business Media. 2012. pp. 60 de 507. ISBN 9789401109246. Consultado el 24 de noviembre de 2019.
Bibliografía
editar- Grünbaum, B.; Polyhedra with hollow faces, Proc. NATO-ASI Conf. on polytopes: abstract, convex and computational, Toronto 1983, Ed. Bisztriczky, T. Et Al., Kluwer Academic (1994), pp. 43–70.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Archivado el 3 de agosto de 2016 en Wayback Machine. Discrete and Computational Geometry: The Goodman-Pollack Festschrift. B. Aronov, S. Basu, J. Pach, and Sharir, M., eds. Springer, New York 2003, pp. 461–488.