Quimiometría
La quimiometría es la disciplina química que tiene como misión extraer información de sistemas químicos mediante el tratamiento estadístico y matemático de los datos procedentes de las diferentes observaciones experimentales. No obstante, la quimiometría es inherentemente interdisciplinaria ya que utiliza metodología frecuentemente empleada en otras disciplinas básicas como análisis de datos, estadística multivariante, deconvolución de señales e informática (entre otras muchas), para abordar problemas de química, bioquímica, medicina, biología e ingeniería química.
Introducción
editarLa notación "quimiometría" tiene su origen en la palabla inglesa "chemometrics", término introducido en 1972 por el científico sueco Svante Wold y el norteamericano Bruce R. Kowalski. Estos mismos autores fundaron dos años después la International Chemometrics Society (ICS), que en 1975 propuso la definición de quimiometría[1]:
... la disciplina química que utiliza métodos matemáticos y estadísticos tanto para diseñar o seleccionar los experimentos y procedimientos más adecuados como para obtener la máxima información química a partir de los datos químicos obtenidos.
En esta primera etapa, aunque todavía relativamente pocos químicos se identificaban con la quimiometría, algunos grupos de científicos entusiastas se lanzaron a promover el nombre y la idea con lo que el término quimiometría comenzó a ser utilizado con cierta frecuencia, sobre todo por aquellos químicos que se dedicaban a la evaluación de datos procedentes de medidas analíticas, ya que lo encontraron especialmente útil en estudios de análisis multivariante o en determinaciones cuantitativas simultáneas de varios componentes (calibración multivariante y análisis multicomponente). En aquella época, la mayoría de los usuarios de la quimiometría, en realidad eran programadores bastante expertos usuarios de la computadora central de sus centros de investigación o, posteriormente, utilizando caros ordenadores personales primitivos, de muy baja capacidad y escasa velocidad de procesamiento. Estos pioneros a menudo tenían que desarrollar sus propios programas de cálculo, pues no existían paquetes estadísticos o de otro software relacionado con la quimiometría. Es a partir de la década de 1980, como consecuencia de una mayor facilidad de acceso a los ordenadores personales, cuando se inicia una nueva era para la quimiometría. A ello contribuyó una reunión de expertos patrocinado por la OTAN y que tuvo lugar en Cosenza (Italia) en 1983[2], tras el cual los acontecimientos se desarrollaron rápidamente, apareciendo las primeras revistas científicas especializadas Journal of Chemometrics, Chemometrics and Intelligent Laboratory Systems, and Journal of Chemical Information and Modeling, además de varios e importantes libros y monografías como la primera edición del libro de Malinowski; Factor Analysis in Chemistry,[3], la primera edición del libro de Sharaf, Illman and Kowalski titulado Chemometrics,[4], el libro de Massart y colaboradores; Chemometrics: a textbook[5], o el libro monográfico dedicado a la calibración multivariante publicado por Martens and Naes[6], a la vez que empezaron a surgir importantes paquetes de software como The Unscrambler o SIMCA.
Métodos quimiométricos
editarEn principio la quimiometría hace uso de cualquier herramienta matemática o estadística, lo que lleva a que la investigación en esta disciplina abarque un amplio campo de diferentes métodos que pueden ser aplicados en química. Aunque la mayoría de estos métodos tienen nombre en español o han sido castellanizados, los científicos que hacen uso de estas herramientas, a menudo se refieren a ellas por sus siglas en inglés. A continuación se describen brevemente los principales métodos utilizados agrupados en diferentes áreas:
Calibración multivariante.
editarEn el análisis moderno es muy frecuente el empleo de técnicas instrumentales. Por otro lado, el empleo de estas técnicas requiere, como paso preliminar a su aplicación, el calibrado del instrumento, ya que es preciso conocer de antemano la relación que existe entre la concentración o la cantidad de analito y la señal analítica proporcionada por dicho instrumento. En este caso, el objetivo de la quimiometría es desarrollar modelos matemáticos capaces de predecir estas relaciones señal instrumental/concentración de analitos mediante el empleo simultáneo de múltiples señales espectrales. El proceso global, implica partir de un conjunto de muestras con contenidos conocidos de los analitos de interés (muestras de referencia o muestras patrón)y con ellas construir el modelo matemático que permita, posteriormente, determinar la concentración de esos analitos en nuevas muestras con contenidos de analito no conocidos previamente.
Los métodos de calibración multivariante se suelen clasificar en métodos de regresión clásica (CLS o MLR) por sus nombres en inglés (Classical Least Squares o Multiple Linear Regression ) y en métodos de regresión inversa, como por ejemplo la Regresión Lineal de Componentes Principales (PCR) o la Regresión Lineal de Mínimos Cuadrados Parciales (PLS)[6] [7].
La principal diferencia entre estos dos enfoques es que en la calibración clásica los modelos se obtienen relacionando la señal analítica, como variable dependiente, con la concentración o con la propiedad que va a ser determinada, de la misma forma que se hace en los procedimientos de calibración univariante mediante regresión lineal (una sola señal espectral y un solo componente). Por el contrario, en la calibración inversa es la concentración del analito la que se modela como una función de la señal instrumental[8]. Así, mientras que los métodos clásicos requieren disponer de conocimientos previos de cómo se relaciona la señal instrumental con la propiedad a determinar (como en el caso de la ley de Beer en espectrofotometría), en el caso de los métodos inversos no es necesario este nivel de conocimiento y, en teoría, son capaces de proporcionar mejores predicciones, lo que hace que los métodos inversos se apliquen con mayor frecuencia.
La principal utilidad de la calibración multivariante es la determinación multicomponente de muestras no excesivamente complejas, ya que permite determinar varios analitos de forma simultánea sin necesidad de separaciones previas mediante el empleo de técnicas más complejas como la cromatografía líquida.
Clasificación, reconocimiento de pautas y análisis de agrupamientos
editarEn la actualidad los químicos disponen de avanzados y sofisticados medios instrumentales capaces de suministrar grandes cantidades de datos relativos a los analitos presentes en una muestra, así como de sus propiedades físico-químicas. Así, p.ej., un analizador automático de sangre, de los que se utilizan en un laboratorio clínico, es capaz de determinar el contenido en suero y plasma de una veintena de analitos de interés clínico, que junto con los datos hematológicos y los obtenidos mediante los analizadores de orina pueden suponer un total de cuarenta datos por paciente. Cualquier espectrómetro moderno (IR, espectrofotómetro, etc.) en un solo barrido puede obtener miles de datos de intensidad o de absorción de la radiación de una sola muestra, a la vez de que son capaces de analizar multitud de muestras en periodos de tiempo relativamente corto. En química analítica, esta cantidad ingente de datos, puede ser utilizada para clasificar muestras, buscar similitudes o diferencias entre ellas o agruparlas según sus similitudes[9]. El conjunto de métodos matemáticos que pueden ser utilizados con esto fines recibe el nombre de Análisis Multivariante, que podría ser definido como “conjunto de métodos y herramientas estadísticas utilizadas para evaluar la contribución de un conjunto de factores o variables en los resultados analíticos”. Si este análisis multivariante se hace con el único y exclusivo fin de conocer cómo se relacionan entre sí las muestras u objetos analizados, buscando diferencias y similitudes entre ellos, se trataría de un reconocimiento de pautas no supervisado. Por el contrario, si de antemano ya se conoce la relación existente entre las muestras que forman los grupos y las causas que hacen que estos tengas propiedades similares, entonces se dice que el reconocimiento de pautas es supervisado.
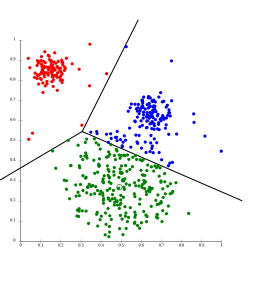
El análisis multivariante se asienta sobre el principio de que los objetos o muestras sometidas a evaluación, cuando son similares presentan valores muy parecidos de ciertas propiedades medibles, es decir, presentas similares pautas. En los procedimiento no supervisados, esta similitud o diferencias se suelen expresar en términos de distancias vectoriales entre los diferentes objetos analizados y para realizarlos se utilizan diferentes métodos matemáticos, el más sencillo y simple es medir las distancias euclídeas entre cada objeto y todos los demás y una vez conocidas estas, generar un diagrama jerarquizado que recibe el nombre de dendrograma a partir del cual se deducen los diferentes agrupamientos de las muestras según sus características, de ahí que este procedimiento reciba comúnmente el nombre de análisis de agrupamientos o análisis clúster. Este procedimiento solo da información sobre las similitudes o diferencias entre muestras u objetos sin considerar el modo en que estas se relacionan con las variables que han generado los agrupamientos o la relación existente entre las diferentes variables. Cuando se requiere disponer de esta información, se recurre a procedimientos de reducción dimensional, como el análisis de componentes principales (PCA) o al análisis de factores (FA), en que las muestras se representan como puntos o “scores” y los vectores (“loadings”) proyectados sobre sus componentes principales[10].
Respecto a los procedimientos supervisados de clasificación, estos están estrechamente relacionadas con los procedimientos de calibración multivariante, en el sentido de que se utiliza un conjunto de calibración o entrenamiento para desarrollar un modelo matemático capaz de clasificar muestras futuras. Entre los métodos utilizados en quimiometría destacan el análisis discriminante lineal, la máquina de aprendizaje lineal y las redes neuronales artificiales.
Tratamiento de señales
editarEn el análisis moderno, la mayoría de los datos se obtienen en formato digital, como espectros, cromatogramas, voltamperogramas, etc. que son almacenados por la computadora para su posterior registro en dominios de frecuencia, longitud de onda, de tiempo, etc. La mayoría de estas señales analíticas requieren de un tratamiento matemático previo a su posterior uso en calibración o clasificación. Estos tratamientos incluyen el filtrado y suavizado de señales mediante métodos matemáticos más o menos sencillos como el filtrado mediante promedios móviles u otros más complejos, como el suavizado polinomial mediante el filtro de Savitzky-Golay o el filtro de Kalman. También se incluyen en esta área de aplicación de la quimiometría, la integración y la derivación matemática de series de datos o las tranformaciones de estas mediante el empleo de algoritmos de transformada de Fourier o de Hadamard.
Resolución multivariante de curvas
editarEn la resolución de curvas generalmente se busca la deconvolución de las señales obtenidas por los instrumentos cuando estas proceden de varias sustancias presentes en la muestra y que de forma individual muestran señales similares, aunque suficientemente diferenciadas como para que pueda ser estimada la contribución de cada uno de los componentes en el resultado final, que sería la señal medida. Esta situación se da con mucha frecuencia en el análisis espectral de sustancias moleculares, ya que generalmente muestran bandas anchas de absorción o de emisión de radiación electromagnética. Así, por ejemplo, a partir de un conjunto de datos que comprende espectros de fluorescencia de una serie de muestras, cada una de las cuales conteniendo múltiples fluoróforos, se pueden usar métodos multivariantes para extraer los espectros de fluorescencia de los fluoróforos individuales, como si estos se hubieran obtenido a partir de los componentes individuales por separado. Es precisamente este campo de la espectrometría uno de los más beneficiados por el empleo de métodos de resolución multivariante de curvas[11][12].
Diseño experimental y optimización
editarA menudo en los laboratorios de investigación se requiere poner a punto nuevos métodos para los que se necesita realizar determinados experimentos científicos. Es en este aspecto de la química donde incide esta área de la quimiometría. El término diseño experimental se utiliza habitualmente para describir las diferentes etapas de este proceso de puesta a punto de nuevos procedimientos: identificación de factores que afectan al resultado final; diseño de los experimentos de modo que se minimicen los efectos de aquellos factores no controlados y, finalmente, tomar decisiones sobre cuáles son las condiciones óptimas en que se puede llevar a cabo el proceso químico estudiado (análisis, síntesis de alguna sustancia, rendimiento de una reacción, etc.).
Para evitar en lo posible la subjetividad del científico, tanto el diseño o diseños iniciales como en la toma de las decisiones finales se siguen unas determinadas normas, generalmente basadas en criterios estadísticos. Los procesos de optimización pueden ser de dos tipos: los basados en diseños secuenciales y lo que utilizan de diseños simultáneos como punto de partida. Los diseños secuenciales se caracterizan por partir de un número reducido de experimentos iniciales realizados bajo determinadas condiciones. En función de los resultados obtenidos en estos experimentos se van desechando algunas condiciones de trabajo y añadiendo otras nuevas en sucesivos experimentos hasta encontrar las condiciones óptimas. Muchos de los métodos de este tipo están basados en el procedimiento de optimización mediante geometría Simplex, inicialmente propuesto por Spendley[13]. Respecto a los diseños simultáneos, al contrario de lo que ocurre con los métodos secuenciales, en primer lugar se planifican todos los experimentos que se van a realizar y no es hasta después de haber obtenido todas las respuestas o resultados experimentales, cuando se decide cuáles son las condiciones óptimas. La mayoría de estos procedimientos están basados en diseños factoriales o variantes de estos, como los diseños compuestos centrados o los diseños de mezclas[14].
Además de los métodos comentados anteriormente, la quimiometría recurre con mucha frecuencia a otros métodos estadísticos, como los diferentes ensayos de hipótesis, el análisis de la varianza (ANOVA), el análisis de correlaciones (CA), métodos de análisis espacial y geoestadística, métodos de estadística de muestreo, gráficos y estadística de control de procesos, validación de cruce y otros muchos.
Véase también
editarReferencias
editar- ↑ Otto, Matthias (2017). «1.- What is chemometrics». Chemometrics. Statistics and Computer Application in Analytical Chemistry (en inglés). Weinheim, Germany: Wiley-VCH. ISBN 978-3-527-34097-2.
- ↑ Brereton, Richard G. (2018). «1. Introduction». Chemometrics. Data Driven Extraction for Science (en inglés). Chichester (UK): John Wiley & Sons.
- ↑ Malinowski, E. R.; Howery, D. G. (1980). Factor Analysis in Chemistry (en inglés). Wiley. ISBN 978-0471058816.
- ↑ Sharaf, M. A.; Illman, D. L.; Kowalski, B. R., eds., ed. (1986). Chemometrics (en inglés). Nueva York: Wiley. ISBN 978-0471831068.
- ↑ Massart, D. L.; Vandeginste, B. G. M.; Deming, S. M.; Michotte, Y.; Kaufman, L. (1988). Chemometrics: a textbook (en inglés). Amsterdam: Elsevier. ISBN 978-0444426604.
- ↑ a b Martens, H.; Naes, T. (1989). Multivariate Calibration (en inglés). Nueva York: Wiley. ISBN 978-0471909798.
- ↑ Franke, J. (2002). «Inverse Least Squares and Classical Least Squares Methods for Quantitative Vibrational Spectroscopy». En Chalmers, John M., ed. Handbook of Vibrational Spectroscopy (en inglés). New York: Wiley. ISBN 978-0471988472.
- ↑ Miller, J.N. y Miller J. C. (2002). Estadística y Quimiometría para Química Analítica. Madrid: Prentice Hall. pp. 239-242. ISBN 84-205-3514-1.
- ↑ Miller, J.N. y Miller J.C. (2002). «Cap. 8. Análisis Multivariante». Estadística y Quimiometría para Química Analítica. Madrid: Prentice Hall. ISBN 84-205-3514-1.
- ↑ Pérez-Arribas L.V., León-González M.A., and Rosales-Conrado N. (2017). «Learning Principal Component Analysis by using data Air Quality Network». Journal Chemical Education (en inglés) 94: 458-467. doi:10.1021/acs.jchemed.6b00550.
- ↑ Malinowski, E. R. (1991). Factor Analysis in Chemistry (en inglés) (2 edición). New York: Wiley.
- ↑ de Juan, A.; Tauler, R. (2006). «Multivariate Curve Resolution (MCR) from 2000: Progress in Concepts and Applications». Critical Reviews in Analytical Chemistry (en inglés). 3-4: 163-176. doi:10.1080/10408340600970005.
- ↑ W. Spendley, G.R. Hext and F.R. Himsworth (1962). «Sequential Application of Simplex Designs in Optimisation and Evolutionary Operation». Technometrics 4 (4): 441-461.
- ↑ Brereton, Richard G. (2003). «Cap.2 Experimental Design». Chemometrics (en inglés). New York: John Wiley and Sons. ISBN 0-471-48977-8.
Bibliografía
editar- Ramis Ramos G. y García Alvarez-Coque Mª C. (2001). Quimiometría. Madrid: Síntesis. ISBN 84-7738-904-7.
- Miller, J.N. y Miller, J.C. (2002). Estadística y Quimiometría para Química Analítica. Madrid: Prentice Hall. ISBN 84-205-3514-1.
- Mongay Fernández, Carlos (2005). Quimiometría. PUV. ISBN 84-370-5923-2.
- Matthias, Otto (2017). Chemometrics. Statistics and Computer Application in Analytical Chemistry (en inglés). New York: Wiley-VCH. ISBN 978-3-527-34097-2.
Enlaces externos
editar