Reconexión magnética

La "reconexión magnética" es un proceso físico que ocurre en plasmas altamente conductores en el que la topología magnética se reorganiza y la energía magnética se convierte en energía cinética, energía térmica y aceleración de partículas. La reconexión magnética se produce en escalas de tiempo intermedias entre la lenta difusión resistiva del campo magnético y las rápidas Alfvénicas.

Reconexión magnética: Esta vista es una sección transversal a través de cuatro dominios magnéticos sometidos a reconexión Parker-Sweet separadora. Dos separatrices (ver texto) dividen el espacio en cuatro dominios magnéticos con un separador en el centro de la figura. Las líneas de campo (y el plasma asociado) fluyen hacia el interior desde encima y debajo del separador, se reconectan y saltan hacia el exterior a lo largo de la hoja de corriente. Mediciones espaciales in situ en la magnetosfera​ y experimentos con plasma en laboratorio​ significan que este proceso se comprende cada vez mejor: una vez iniciado, procede muchos órdenes de magnitud más rápido de lo previsto por la teoría Parker-Sweet.

Evolución de la reconexión magnética durante una erupción solar.​

El concepto de reconexión magnética se introdujo por primera vez en 1950 en la tesis doctoral de James Dungey para explicar el acoplamiento de masa, energía y momento del viento solar en la magnetosfera terrestre.​ y se publicó por primera vez en la literatura abierta en su artículo seminal de 1961.​

Principios fundamentales

La reconexión magnética es un fallo de la "magnetohidrodinámica ideal" y por tanto del "teorema de Alfvén" (también llamado "teorema del flujo congelado") que se aplica a regiones a gran escala de un magnetoplasma altamente conductor, para el que el Número de Reynolds magnético es muy grande: esto hace que el término convectivo en la ecuación de inducción domine en dichas regiones. El teorema del flujo congelado afirma que en tales regiones el campo se mueve con la velocidad del plasma (la media de las velocidades de iones y electrones, ponderada por su masa). El fallo de reconexión de este teorema ocurre en regiones de gran cizalladura magnética (por la ley de Ampére son hojas de corrientes) que son regiones de pequeña anchura donde el Número de Reynolds magnético puede llegar a ser lo suficientemente pequeño como para hacer que el término de difusión en la ecuación de inducción domine, lo que significa que el campo se difunde a través del plasma desde regiones de alto campo a regiones de bajo campo. En la reconexión, las regiones de flujo de entrada y de salida obedecen ambas al teorema de Alfvén y la región de difusión es una región muy pequeña en el centro de la lámina de corriente donde las líneas de campo se difunden juntas, se fusionan y se reconfiguran de tal manera que se transfieren desde la topología de las regiones de flujo de entrada (es decir, a lo largo de la lámina de corriente) a la de las regiones de flujo de salida (es decir, enhebrando la lámina de corriente). La velocidad de esta transferencia de flujo magnético es el campo eléctrico asociado tanto al flujo de entrada como al de salida y se denomina "velocidad de reconexión".​​

La equivalencia de cizalladura magnética y corriente puede verse a partir de una de las ecuaciones de Maxwell

$\nabla \times \mathbf {B} =\mu \mathbf {J} +\mu \epsilon {\frac {\partial \mathbf {E} }{\partial t}}.$

En un plasma (gas ionizado), para todos los fenómenos excepto excepcionalmente alta frecuencia, el segundo término en el lado derecho de esta ecuación, la corriente de desplazamiento, es despreciable en comparación con el efecto de la corriente libre $\mathbf {J}$ y esta ecuación se reduce a la ley de Ampére para cargas libres. La corriente de desplazamiento se desprecia tanto en los tratamientos teóricos de Parker-Sweet y Petschek de la reconexión, discutidos más adelante, como en la derivación del MHD ideal y el teorema de Alfvén que se aplica en esas teorías en todas partes fuera de la pequeña región de difusión.

La resistividad de la capa de corriente permite que el flujo magnético de cualquier lado se difunda a través de la capa de corriente, anulando el flujo de salida del otro lado de la frontera. Sin embargo, la pequeña escala espacial de la lámina de corriente hace que el Número de Reynolds magnético sea pequeño, por lo que esto por sí solo puede hacer que el término de difusión domine en la ecuación de inducción sin que la resistividad se vea aumentada. Cuando las líneas de campo difusoras de los dos sitios de la frontera se tocan forman las separatrices y así tienen tanto la topología de la región de entrada (es decir, a lo largo de la hoja de corriente) como la región de salida (es decir, enhebrando la hoja de corriente). En la reconexión magnética, las líneas de campo evolucionan desde la topología de afluencia a través de la topología de separatrices hasta la topología de flujo de salida. Cuando esto ocurre, el plasma es arrastrado hacia fuera por la Fuerza de tensión magnética que actúa sobre las líneas de campo reconfiguradas y las expulsa a lo largo de la hoja de corriente. La caída de presión resultante atrae más plasma y flujo magnético hacia la región central, dando lugar a un proceso autosostenido. La importancia del concepto de Dungey de una ruptura localizada del MHD ideal radica en que el flujo de salida a lo largo de la hoja de corriente evita la acumulación de presión en el plasma que, de otro modo, ahogaría el flujo de entrada. En la reconexión Parker-Sweet, el flujo de salida se produce sólo a lo largo de una fina capa en el centro de la lámina de corriente, lo que limita la velocidad de reconexión a valores bajos. Por otro lado, en la reconexión Petschek la región de flujo de salida es mucho más amplia, encontrándose entre frentes de choque (ahora se piensa que son ondas de Alfvén) que se encuentran en el flujo de entrada: esto permite un escape mucho más rápido del plasma congelado en las líneas de campo reconectadas y la tasa de reconexión puede ser mucho mayor.

Dungey acuñó el término "reconexión" porque inicialmente preveía que las líneas de campo de la topología de afluencia se rompieran y luego se unieran de nuevo en la topología de flujo de salida. Sin embargo, esto significa que existirían monopolos magnéticos, aunque durante un periodo muy limitado, lo que violaría las Ecuaciones de Maxwell de que la divergencia del campo es cero. Sin embargo, al considerar la evolución a través de la topología de la separatriz, se evita la necesidad de invocar monopolos magnéticos. Los modelos numéricos globales MHD de la magnetosfera, que utilizan las ecuaciones del MHD ideal, siguen simulando la reconexión magnética a pesar de que se trata de una ruptura del MHD ideal.​ La razón se acerca a las ideas originales de Dungey: en cada paso temporal del modelo numérico se resuelven las ecuaciones de MHD ideal en cada punto de la rejilla de la simulación para evaluar las nuevas condiciones del campo y del plasma. Las líneas de campo magnético tienen que ser trazadas de nuevo. El algoritmo de trazado comete errores en las láminas de corriente delgadas y une las líneas de campo enhebrándolas donde antes estaban alineadas con la lámina de corriente. Esto suele denominarse "resistividad numérica" y las simulaciones tienen valor predictivo porque el error se propaga según una ecuación de difusión.

Un problema actual en física de plasmas es que la reconexión observada ocurre mucho más rápido de lo predicho por MHD en plasmas de número de Lundquist alto (es decir, reconexión magnética rápida). Las fulguraciones solares, por ejemplo, se producen 13-14 órdenes de magnitud más rápido de lo que sugeriría un cálculo ingenuo, y varios órdenes de magnitud más rápido que los modelos teóricos actuales que incluyen turbulencia y efectos cinéticos. Un posible mecanismo para explicar la discrepancia es que la turbulencia electromagnética en la capa límite sea lo suficientemente fuerte como para dispersar electrones, aumentando la resistividad local del plasma. Esto permitiría que el flujo magnético se difundiera más rápidamente.

Propiedades

Evento de reconexión magnética en el sol

Interpretación física

La descripción cualitativa del proceso de reconexión es tal que las líneas de campo magnético de diferentes dominios magnéticos (definidos por la conectividad de las líneas de campo) se empalman entre sí, cambiando sus patrones de conectividad con respecto a las fuentes. Se trata de una violación de una ley de conservación aproximada en física de plasmas, llamada teorema de Alfvén (también llamada "MHD ideal" del "teorema del flujo congelado") y puede concentrar energía mecánica o magnética tanto en el espacio como en el tiempo. Las erupciones solares, las mayores explosiones del Sistema Solar, pueden implicar la reconexión de grandes sistemas de flujo magnético en el Sol, liberando, en cuestión de minutos, energía que ha estado almacenada en el campo magnético durante un periodo de horas a días. La reconexión magnética en la magnetosfera de la Tierra es uno de los mecanismos responsables de la aurora polar, y es importante para la ciencia de la fusión nuclear controlada porque es uno de los mecanismos que impiden el confinamiento magnético del combustible de fusión.

En un plasma conductor de la electricidad, las líneas de campo magnético se agrupan en "dominios": haces de líneas de campo que se conectan desde un lugar concreto a otro lugar concreto y que son topológicamente distintas de otras líneas de campo cercanas. Esta topología se conserva aproximadamente incluso cuando el propio campo magnético está fuertemente distorsionado por la presencia de corrientes variables o el movimiento de fuentes magnéticas, porque los efectos que de otro modo podrían cambiar la topología magnética inducen corrientes parásitas en el plasma; las corrientes parásitas tienen el efecto de cancelar el cambio topológico.

Tipos de reconexión

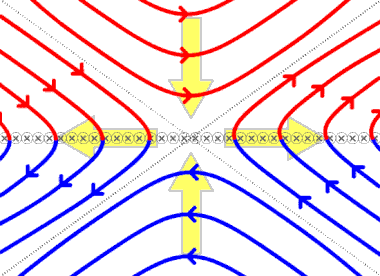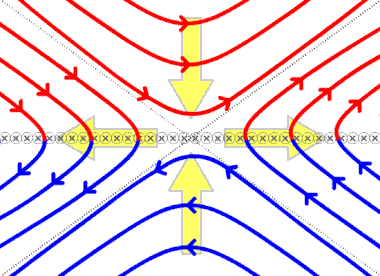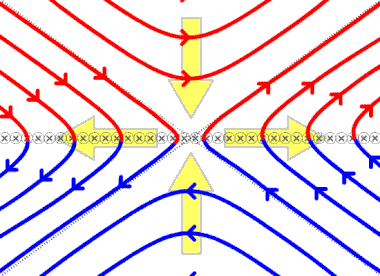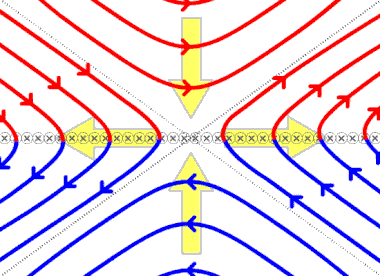
En dos dimensiones, el tipo más común de reconexión magnética es la reconexión separadora, en la que cuatro dominios magnéticos separados intercambian líneas de campo magnético. Los dominios en un plasma magnético están separados por superficies separatrix]: superficies curvas en el espacio que dividen diferentes haces de flujo. Las líneas de campo en un lado de la separatriz terminan todas en un polo magnético particular, mientras que las líneas de campo en el otro lado terminan todas en un polo diferente de signo similar. Dado que cada línea de campo comienza generalmente en un polo magnético norte y termina en un polo magnético sur, la forma más general de dividir sistemas de flujo simples implica cuatro dominios separados por dos separatrices: una superficie de la separatriz divide el flujo en dos haces, cada uno de los cuales comparte un polo sur, y la otra superficie de la separatriz divide el flujo en dos haces, cada uno de los cuales comparte un polo norte. La intersección de las separatrices forma un separador, una única línea que se encuentra en el límite de los cuatro dominios separados. En la reconexión de separatrices, las líneas de campo entran en el separador desde dos de los dominios, y se empalman una con otra, saliendo del separador en los otros dos dominios (véase la primera figura).

En tres dimensiones, la geometría de las líneas de campo se vuelve más complicada que en el caso bidimensional y es posible que se produzca reconexión en regiones donde no existe separador, pero con las líneas de campo conectadas por gradientes pronunciados.​ Estas regiones se conocen como capas cuasi-separadoras (QSL)', y se han observado en configuraciones teóricas​ y las erupciones solares.​​

Descripciones teóricas

Reconexión lenta: Modelo de Sweet-Parker

El primer marco teórico de la reconexión magnética fue establecido por Peter Sweet y Eugene Parker en una conferencia en 1956. Sweet señaló que al empujar dos plasmas con campos magnéticos dirigidos opuestamente entre sí, la difusión resistiva es capaz de ocurrir en una escala de longitud mucho más corta que una escala de longitud de equilibrio típica.​ Parker asistió a esta conferencia y desarrolló relaciones de escala para este modelo durante su viaje de regreso.​

El modelo Sweet-Parker describe la reconexión magnética independiente del tiempo en el marco MHD resistivo cuando los campos magnéticos de reconexión son antiparalelos (dirigidos opuestamente) y los efectos relacionados con la viscosidad y la compresibilidad no son importantes. La velocidad inicial es simplemente una velocidad $E\times B$, por lo que

$E_{y}=v_{\text{in}}B_{\text{in}}$

donde $E_{y}$ es el campo eléctrico fuera del plano, $v_{\text{in}}$ es la velocidad de afluencia característica, y $B_{\text{in}}$ es la intensidad de campo magnético característica aguas arriba. Despreciando la corriente de desplazamiento, la ley de Ampere de baja frecuencia, $\mathbf {J} ={\frac {1}{\mu _{0}}}\nabla \times \mathbf {B}$ da la relación

$J_{y}\sim {\frac {B_{\text{in}}}{\mu _{0}\delta }},$

donde $\delta$ es el semiespesor de la lámina de corriente. Esta relación utiliza que el campo magnético se invierte sobre una distancia de $\sim 2\delta$. Haciendo coincidir el campo eléctrico ideal fuera de la capa con el campo eléctrico resistivo $\mathbf {E} ={\frac {1}{\sigma }}\mathbf {J}$ dentro de la capa (usando la ley de Ohm), encontramos que

$v_{\text{in}}={\frac {E_{y}}{B_{\text{in}}}}\sim {\frac {1}{\mu _{0}\sigma \delta }}={\frac {\eta }{\delta }},$

donde $\eta$ es la difusividad magnética. Cuando la densidad de entrada es comparable a la densidad de salida, la conservación de la masa produce la relación

$v_{\text{in}}L\sim v_{\text{out}}\delta ,$

donde $L$ es la semilongitud de la lámina de corriente y $v_{\text{out}}$ es la velocidad de salida. Los lados izquierdo y derecho de la relación anterior representan el flujo de masa hacia la capa y hacia fuera de la capa, respectivamente. Igualando la presión magnética aguas arriba con la presión dinámica aguas abajo se obtiene

${\frac {B_{\text{in}}^{2}}{2\mu _{0}}}\sim {\frac {\rho v_{\text{out}}^{2}}{2}}$

donde $\rho$ es la densidad de masa del plasma. Resolviendo para la velocidad de salida se obtiene entonces

$v_{\text{out}}\sim {\frac {B_{\text{in}}}{\sqrt {\mu _{0}\rho }}}\equiv v_{A}$

donde $v_{A}$ es la velocidad de Alfvén. Con las relaciones anteriores, la tasa adimensional de reconexión $R$ puede entonces escribirse en dos formas, la primera en términos de $(\eta ,\delta ,v_{A})$ usando el resultado derivado anteriormente de la ley de Ohm, la segunda en términos de $(\delta ,L)$ a partir de la conservación de la masa como

$R={\frac {v_{\text{in}}}{v_{\text{out}}}}\sim {\frac {\eta }{v_{A}\delta }}\sim {\frac {\delta }{L}}.$

Dado que el número de Lundquist adimensional. $S$ viene dado por

$S\equiv {\frac {Lv_{A}}{\eta }},$

las dos expresiones diferentes de $R$ se multiplican entre sí y luego se elevan al cuadrado, dando una relación simple entre la tasa de reconexión $R$ y el número de Lundquist $S$.

$R~\sim {\sqrt {\frac {\eta }{v_{A}L}}}={\frac {1}{S^{\frac {1}{2}}}}.$

La reconexión Sweet-Parker permite tasas de reconexión mucho más rápidas que la difusión global, pero no es capaz de explicar las rápidas tasas de reconexión observadas en las erupciones solares, la magnetosfera terrestre y los plasmas de laboratorio. Además, la reconexión Sweet-Parker no tiene en cuenta los efectos tridimensionales, la física sin colisiones, los efectos dependientes del tiempo, la viscosidad, la compresibilidad y la presión descendente. Las simulaciones numéricas de la reconexión magnética bidimensional suelen coincidir con este modelo.​ Los resultados del Experimento de Reconexión Magnética (MRX) de reconexión colisional muestran concordancia con un modelo generalizado de Sweet-Parker que incorpora compresibilidad, presión aguas abajo y resistividad anómala.​​

Reconexión rápida: Modelo Petschek

La razón fundamental por la que la reconexión Petshek es más rápida que la Parker-Sweet es que amplía la región de flujo de salida y elimina así parte de la limitación causada por la acumulación de presión en el plasma. La velocidad de entrada, y por tanto la velocidad de reconexión, sólo puede ser muy pequeña si la región de salida es estrecha. En 1964, Harry Petschek propuso un mecanismo en el que las regiones de flujo de entrada y de salida están separadas por choques estacionarios de modo lento que se encuentran en los flujos de entrada.​ La relación de aspecto de la región de difusión es entonces del orden de la unidad y la tasa de reconexión máxima se convierte en

${\frac {v_{\text{in}}}{v_{A}}}\approx {\frac {\pi }{8\ln S}}.$

Esta expresión permite una reconexión rápida y es casi independiente del número de Lundquist. La teoría y las simulaciones numéricas demuestran que la mayor parte de las acciones de los choques que propuso Petshek pueden llevarse a cabo mediante ondas Alfvén y, en particular, discontinuidades rotacionales (RD). En los casos de densidades de plasma asimétricas en los dos lados de la lámina de corriente (como en la magnetopausa diurna de la Tierra) la onda de Alfvén que se propaga en el flujo de entrada en el lado de mayor densidad (en el caso de la magnetopausa la magnetosfera más densa) tiene una velocidad de propagación más baja y por lo tanto la rotación del campo se hace cada vez más en ese RD como la línea de campo se propaga lejos del sitio de reconexión: por lo tanto, la lámina de corriente de la magnetopausa se concentra cada vez más en el exterior, más lento, RD.

Las simulaciones de reconexión MHD resistiva con resistividad uniforme mostraron el desarrollo de láminas de corriente alargadas de acuerdo con el modelo Sweet-Parker más que con el modelo Petschek. Sin embargo, cuando se utiliza una resistividad anómala localizada, la reconexión Petschek puede realizarse en simulaciones MHD resistivas. Dado que el uso de una resistividad anómala sólo es apropiado cuando el camino libre medio de la partícula es grande en comparación con la capa de reconexión, es probable que otros efectos sin colisión se vuelvan importantes antes de que se pueda realizar la reconexión Petschek.

Resistividad anómala y difusión de Bohm

En el modelo de Sweet-Parker, la suposición común es que la difusividad magnética es constante. Esto se puede estimar usando la ecuación de movimiento para un electrón con masa $m$ y carga eléctrica $e$:

${d{\mathbf {v} } \over dt}={e \over m}\mathbf {E} -\nu \mathbf {v} ,$

donde $\nu$ es la frecuencia de colisión. Como en el estado estacionario, $d{\mathbf {v} }/dt=0$, entonces la ecuación anterior junto con la definición de corriente eléctrica, ${\mathbf {J} }=en{\mathbf {v} }$, donde $n$ es la densidad del número de electrones, da como resultado

$\eta =\nu {c^{2} \over \omega _{pi}^{2}}.$

Sin embargo, si la velocidad de deriva de los electrones supera la velocidad térmica del plasma, no se puede alcanzar un estado estacionario y la difusividad magnética debe ser mucho mayor que la dada en lo anterior. Esto se denomina resistividad anómala, $\eta _{\text{anom}}$, que puede aumentar la velocidad de reconexión en el modelo de Sweet-Parker en un factor de $\eta _{\text{anom}}/\eta$.

Otro mecanismo propuesto se conoce como difusión de Bohm a través del campo magnético. Este sustituye la resistividad óhmica por $v_{A}^{2}(mc/eB)$, sin embargo, su efecto, similar al de la resistividad anómala, sigue siendo demasiado pequeño en comparación con las observaciones.​

Reconexión estocástica

En la reconexión estocástica,​ campo magnético tiene un componente aleatorio de pequeña escala que surge debido a la turbulencia.​ Para el flujo turbulento en la región de reconexión, debe utilizarse un modelo de turbulencia magnetohidrodinámica como el desarrollado por Goldreich y Sridhar en 1995.​ Este modelo estocástico es independiente de la física a pequeña escala, como los efectos resistivos, y depende sólo de los efectos turbulentos.​ A grandes rasgos, en el modelo estocástico, la turbulencia lleva líneas de campo magnético inicialmente distantes a pequeñas separaciones donde pueden reconectarse localmente (reconexión tipo Sweet-Parker) y separarse de nuevo debido a la difusión turbulenta super- lineal turbulenta (difusión de Richardson​). Para una lámina de corriente de la longitud $L$, el límite superior para la velocidad de reconexión viene dado por

$v=v_{\text{turb}}\;\operatorname {min} \left[\left({L \over l}\right)^{\frac {1}{2}},\left({l \over L}\right)^{\frac {1}{2}}\right],$

donde $v_{\text{turb}}=v_{l}^{2}/v_{A}$. Aquí $l$, y $v_{l}$son la escala de longitud de inyección de turbulencia y la velocidad respectivamente y $v_{A}$es la velocidad de Alfvén. Este modelo ha sido probado con éxito mediante simulaciones numéricas.​​

Proceso no-MHD: Reconexión sin colisiones

En escalas de longitud más cortas que la longitud inercial de los iones $c/\omega _{pi}$ donde

$\omega _{pi}\equiv {\sqrt {\frac {n_{i}Z^{2}e^{2}}{\epsilon _{0}m_{i}}}}$

es la frecuencia del plasma de iones), los iones se desacoplan de los electrones y el campo magnético se congela en el fluido de electrones en lugar de en el plasma. A estas escalas, el efecto Hall adquiere importancia. Las simulaciones de dos fluidos muestran la formación de una geometría de punto X en lugar de la geometría de doble punto Y característica de la reconexión resistiva. A continuación, los electrones son acelerados a velocidades muy altas por Ondas de Whistler. Debido a que los iones pueden moverse a través de un "cuello de botella" más amplio cerca de la capa de corriente y debido a que los electrones se mueven mucho más rápido en MHD Hall que en MHD estándar, la reconexión puede proceder más rápidamente. La reconexión de dos fluidos/sin colisión es particularmente importante en la magnetosfera terrestre.