Squircle
Un círculo cuadrado (en inglés Squircle, acrónimo de square y circle) es una forma intermedia entre un cuadrado y un círculo. Existen al menos dos definiciones de 'squircle' en uso, la más común de las cuales se basa en la superelipse. Los squircles se han aplicado en diseño y óptica.
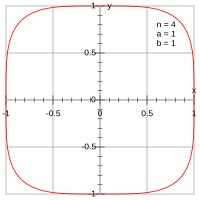
Squircle basado en superelipse
editarEn el sistema de coordenadas cartesianas, la superelipse se define mediante la ecuación
donde ra y rb son el Semieje mayor y el menor, a y b son las coordenadas x e y del centro de la elipse e y n es un número positivo. El squircle se define entonces como la superelipse con ra = rb y n = 4 . Su ecuación es:[1]
donde r es el radio menor del squircle. Compárese esto con la ecuación de una circunferencia. Cuando el squircle está centrado en el origen, entonces a = b = 0, y se denomina cuártico especial de Lamé.
El área dentro del squircle se puede expresar en términos de la función gamma Γ(x) como[1]
donde r es el radio menor del squircle, y es la constante de la lemniscata.
Notación norma p
editarEn términos de norma p ‖ · ‖p en ℝ2, el squircle se puede expresar como:
donde p = 4, xc = (a,b) es el vector que denota el centro del squircle, y x = (x,y). Efectivamente, esto sigue siendo una especie de círculo de puntos a una distancia r del centro, pero la distancia se define de manera diferente. A modo de comparación, el círculo habitual es el caso p = 2, mientras que el cuadrado está dado por el caso p → ∞ (la norma del supremo), y un cuadrado girado está dado por p = 1 (la norma del taxista). Esto permite una generalización sencilla a un cubo esférico, o sphube, en ℝ3, o hipersphubes en dimensiones superiores.[2]
Squircle de Fernández-Guasti
editarOtro problema proviene del trabajo en óptica.[3][4] Se le puede llamar el squircle de Fernández-Guasti, en honor a uno de sus autores, para distinguirla del relacionado con la superelipse anterior.[2] Este tipo de squircle, centrado en el origen, se puede definir mediante la ecuación:
donde r es el menor radio del squircle, s es el parámetro de cuadratura, y x e y son en el intervalo [−r,r]. Si s = 0, la ecuación es un círculo; si s = 1, este es un cuadrado. Esta ecuación permite una parametrización suave de la transición de un círculo a un cuadrado, sin involucrar al infinito.
Formas similares
editarSe puede generar una forma similar a un squircle, llamado cuadrado redondeado, separando cuatro cuartos de un círculo y conectando sus extremos sueltos con líneas rectas, o separando los cuatro lados de un cuadrado y conectándolos con cuartos de círculo. Tal forma es muy similar pero no idéntica a la del squircle. Aunque construir un cuadrado redondeado puede ser conceptual y físicamente más simple, el squircle tiene la ecuación más simple y se puede generalizar mucho más fácilmente. Una consecuencia de esto es que el squircle y otras superelipses se pueden escalar hacia arriba o hacia abajo con bastante facilidad. Esto es útil cuando, por ejemplo, se desea crear squircles anidados.
Otra forma similar es un círculo truncado, el límite de la intersección de las regiones encerradas por un cuadrado y por un círculo concéntrico cuyo diámetro es mayor que la longitud del lado del cuadrado y menor que la longitud de la diagonal del cuadrado (para que cada figura tenga puntos interiores que no estén en el interior de la otra). Tales formas carecen de la continuidad tangente que poseen tanto las superelipsis como los cuadrados redondeados.
Usos
editarLos squircles son útiles en óptica. Si la luz pasa a través de una abertura cuadrada bidimensional, el punto central en el patrón de difracción se puede modelar de cerca mediante un círculo o supercírculo. Si se usa una abertura rectangular, el punto puede aproximarse mediante una superelipse.[4]
Los squircles también se han utilizado para construir platos llanos. Un plato squircular tiene un área más grande (y por lo tanto puede contener más comida) que uno circular con el mismo radio, pero aún ocupa la misma cantidad de espacio en un armario rectangular o cuadrado.[5]
Muchos modelos de teléfonos Nokia se han diseñado con un botón de panel táctil en forma de squircle.[6][7]
El fabricante de automóviles Fiat utilizó numerosos squircles en el diseño interior y exterior de la tercera generación del Panda.[8]
Apple Inc. usa una forma que se asemeja a un squircle como la forma de los íconos de aplicaciones en iOS, iPadOS y macOS (a partir de macOS Big Sur), pero en realidad no es un squircle sino una aproximación de una superelipse quíntica.[9] La misma forma se ve en el botón de inicio en dispositivos iOS con un botón de inicio pero no Touch ID (actualmente solo el iPod Touch).
Una de las formas de los iconos adaptables disponibles en el sistema operativo Android "Oreo" es un squircle.[10]
El logo utilizado por Instagram desde 2016 incluye un squircle que forma el contorno de una cámara.
Véase también
editarReferencias
editar- ↑ a b Weisstein, Eric W. «Squircle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ a b Chamberlain Fong (2016). Squircular Calculations. Bibcode:2016arXiv160402174F. arXiv:1604.02174.
- ↑ M. Fernández Guasti (1992). «Analytic Geometry of Some Rectilinear Figures». Int. J. Educ. Sci. Technol. 23: 895-901.
- ↑ a b M. Fernández Guasti; A. Meléndez Cobarrubias; F.J. Renero Carrillo; A. Cornejo Rodríguez (2005). «LCD pixel shape and far-field diffraction patterns». Optik 116 (6): 265-269. Bibcode:2005Optik.116..265F. doi:10.1016/j.ijleo.2005.01.018. Consultado el 20 de noviembre de 2006.
- ↑ «Squircle Plate». Kitchen Contraptions. Archivado desde el original el 1 de noviembre de 2006. Consultado el 20 de noviembre de 2006.
- ↑ Nokia Designer Mark Delaney mentions the squircle in a video regarding classic Nokia phone designs:
Copia archivada. Archivado desde el original el 6 de enero de 2010. Consultado el 2 de octubre de 2021. - ↑ «Clayton Miller evaluates shapes on mobile phone platforms». Consultado el 2 de julio de 2011.
- ↑ «PANDA DESIGN STORY». Archivado desde el original el 24 de abril de 2012. Consultado el 30 de diciembre de 2018.
- ↑ «The Hunt for the Squircle». Consultado el 20 de octubre de 2017.
- ↑ «Adaptive Icons». Consultado el 15 de enero de 2018.