Teoría del caos
La teoría del caos es la rama de la matemática, la física y otras ciencias (biología, meteorología, entre ellas) que trata ciertos tipos de sistemas complejos y sistemas dinámicos no lineales muy sensibles a las variaciones en las condiciones iniciales.

Pequeñas variaciones en dichas condiciones iniciales pueden implicar grandes diferencias en el comportamiento futuro, imposibilitando la predicción a largo plazo. Esto sucede aunque estos sistemas son en rigor deterministas, es decir, su comportamiento puede ser completamente determinado conociendo sus condiciones iniciales.
La disciplina asociada a los sistemas caóticos aclara por qué existe cierto tipo de sistemas cuyo comportamiento es prácticamente imposible de predecir, no sólo porque sean complejos formados por muchos elementos, sino también aclara por qué sistemas relativamente simples y con pocos grados de libertad pueden ser difíciles de predecir a largo plazo.
El comportamiento caótico existe en muchos sistemas naturales, incluyendo el flujo de fluidos, las irregularidades del ritmo cardíaco, el clima y el tiempo.[1] También ocurre espontáneamente en algunos sistemas con componentes artificiales, como el tráfico vehicular. Este comportamiento puede estudiarse mediante el análisis de un modelo matemático caótico o mediante técnicas analíticas como los diagramas de recurrencia y los mapas de Poincaré. La teoría del caos tiene aplicaciones en diversas disciplinas, incluyendo la meteorología, la antropología,[2] la sociología, la ciencia ambiental, la informática, la ingeniería, la economía, la ecología y la gestión de crisis pandémicas.[3][4] La teoría formó la base para campos de estudio como los sistemas complejos, la teoría del borde del caos y los procesos de autoensamblaje.
Clasificación de los sistemas
editarLos sistemas dinámicos se pueden clasificar
- Estables, cuando dos soluciones con condiciones iniciales suficientemente cercanas siguen siendo cercanas a lo largo del tiempo. Así, un sistema estable tiende a lo largo del tiempo a un punto, u órbita, según su dimensión (atractor o sumidero).
- Inestables, cuando dos soluciones con condiciones iniciales diferentes acaban divergiendo por pequeñas que sean las diferencias entre las condiciones iniciales. Así un sistema inestable «escapa» de los atractores.
- Caóticos, cuando el sistema no es inestable y si bien dos soluciones se mantienen a una distancia «finita» cercana a un atractor del sistema dinámico, las soluciones se mueven en torno al atractor de manera irregular y pasado el tiempo ambas soluciones no son cercanas, si bien suelen ser cualitativamente similares. De esa manera, el sistema permanece confinado en una zona de su espacio de estados, pero sin tender a un atractor fijo.
Una de las principales características tanto de los sistemas inestables como los caóticos es que tienen una gran dependencia de las condiciones iniciales (esto diferencia a ambos tipos de los sistemas estables). De un sistema del que se conocen sus ecuaciones de evolución temporal características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distinta. Ejemplos de tales sistemas son el Sistema Solar, las placas tectónicas, los fluidos en régimen turbulento y los incrementos de población.[5]
Caos determinista
editarEl caos determinista comprende una serie de fenómenos encontrados en la teoría de sistemas dinámicos, la teoría de ecuaciones diferenciales y la mecánica clásica. En términos generales el caos determinista da lugar a trayectorias asociadas a la evolución temporal de forma muy irregular y aparentemente azarosa que sin embargo son totalmente deterministas, a diferencia del azar genuino. La irregularidad de las trayectorias está asociada a la imposibilidad práctica de predecir la evolución futura del sistema, aunque esta evolución sea totalmente determinista.
Definición de caos y atractores
editarNo hay una definición universal sobre el caos, pero hay tres ingredientes en los que todos los científicos están de acuerdo:
- Movimiento oscilante. Las trayectorias no se ajustan a un punto fijo, órbita periódica u órbita cuasiperiódica cuando el tiempo tiende a infinito.
- Determinismo. El sistema no es azaroso sino determinista. El comportamiento irregular, en dimensión finita, surge de la no linealidad. Por eso se define como determinista.
- Sensibilidad a las condiciones. Las trayectorias que comienzan cerca, con el tiempo se separan exponencialmente. Es decir, condiciones iniciales muy similares acaban dando lugar a comportamientos diferentes pasado un tiempo suficientemente largo.
Los sistemas caóticos típicamente se caracterizan por ser modelizables mediante un sistema dinámico que posee un atractor. Para definir propiamente un atractor hay que recurrir a tecnicismos, y es difícil dar una idea intuitiva sin ellos. En una primera aproximación puede decirse que un atractor es un conjunto en el que todas las trayectorias cercanas convergen. Los puntos fijos y círculos límite son un ejemplo de ello. Al igual que en la definición del caos, hay 3 ingredientes universales:
- Cualquier trayectoria que esté en un atractor, estará en él para .
- Atraen un conjunto de condiciones iniciales. El conjunto lo componen las condiciones iniciales de su trayectoria que acabe en el atractor cuando .
- No existen condiciones iniciales que satisfagan las dos reglas anteriores.
Dentro de los atractores se define como atractor extraño o caótico al atractor que exhibe dependencia sensible con las condiciones iniciales.
La importancia de la no linealidad en dimensión finita
editarHay dos importantes tipos de sistemas dinámicos: las ecuaciones diferenciales y los sistemas iterativos de funciones. Las ecuaciones diferenciales describen la evolución de un sistema a tiempo real y los mapas iterados evolucionan en problemas donde el tiempo es discreto. Ambos son útiles para dar ejemplos del caos y también para analizar soluciones periódicas o caóticas de las ecuaciones diferenciales.
Se dice que un sistema es no lineal cuando la potencia de las variables de ese sistema es diferente a uno, hay productos entre diferentes variables o funciones de las variables, por ejemplo:
, ,
La mayoría de sistemas no lineales son analíticamente irresolubles. En estos casos se puede lograr alguna solución haciendo una aproximación, pero se pierden soluciones físicas. La razón de que las ecuaciones lineales sean más fáciles de analizar es que los sistemas lineales se pueden separar en partes, resolver cada una de ellas y juntar las soluciones para obtener la solución final. El hecho es que muchos fenómenos en la naturaleza actúan de forma no lineal.
La importancia que tienen los sistemas en el caos es el siguiente: se dice que un sistema dinámico es no sensible cuando pequeños cambios en las condiciones iniciales del sistema no originan grandes cambios en el proceso y resultado final del mismo.
Divergencia exponencial de trayectorias cercanas
editarLos atractores exhiben una dependencia sensible de las condiciones iniciales. Esto significa que dos trayectorias que comienzan cerca una de la otra divergen, y cada una tendrá un futuro totalmente diferente de la otra. Haciendo estudios numéricos de los atractores extraños se puede encontrar la siguiente proporción:
donde es el vector que separa 2 trayectorias, es la separación inicial y es el exponente Lyapunov. Cuando el sistema tiene un exponente de Lyapunov positivo ( ), se encuentra un tiempo de horizonte donde la predicción deja de ser válida. Si se toma como el valor máximo de la distancia aceptable entre dos trayectorias (la predicción será intolerable cuando ), entonces el tiempo de horizonte se define como
Lo peor del tiempo de horizonte es que, por mucho que se minimice la separación inicial, no logrará ser mucho más grande. Esto es, aunque se logre una precisión muy buena, el incremento del tiempo de horizonte que se logra será insignificante comparado con la disminución de . Por esto, Edward Lorenz dijo que era tan difícil predecir el tiempo. Este obstáculo de la predicción se conoce con el nombre efecto mariposa por una charla de Lorenz con el título: ¿Puede el batir de las alas de una mariposa en Brasil dar lugar a un tornado en Texas?.
La sensibilidad a las condiciones es tan extremadamente exagerada que, aparte del provocativo título de la charla de Lorenz, se encuentran otras frases como,
Por perder un clavo, el caballo perdió la herradura, el jinete perdió al caballo, el jinete no combatió, la batalla se perdió, y con ella perdimos el reino.
Si se dibuja una gráfica con los ejes y , se observa que para un corto plazo de , la función se mueve alrededor de una pendiente. El valor de esta pendiente equivale al exponente de Lyapunov. Como se observa en el ejemplo de abajo, después de un tiempo la función no continúa cerca de la pendiente. Esto es debido a que, como el atractor está acotado en un espacio del espacio de fases, la distancia no puede aumentar hasta el infinito.
Atractores
editarEl comportamiento o movimiento en un sistema dinámico puede representarse sobre el espacio de fases. Los diagramas de fases no muestran una trayectoria bien definida, sino que ésta es errabunda alrededor de algún movimiento bien definido. Cuando esto sucede se dice que el sistema es atraído hacia un tipo de movimiento, es decir, que hay un atractor.
Al hablar de atractores no se hace referencia única y exclusivamente a los atractores caóticos, ya que antes de que apareciera el caos se conocían otros tipos de atractores. De acuerdo a la forma en que sus trayectorias evolucionen, los atractores pueden ser clasificados como:
- Atractor de punto fijo: Corresponde al más simple, el sistema que tenga un atractor de punto fijo tenderá a estabilizarse en un único punto. Un ejemplo común es el péndulo, que tiende al punto en el que el ángulo es nulo respecto a la vertical, debido al rozamiento con el aire.
- Atractor de ciclo límite o atractor periódico: Es el segundo tipo de atractor más sencillo. Este tipo de atractor tiende a mantenerse en un periodo igual para siempre. Como ejemplo, se puede tomar un péndulo alimentado para contrarrestar la fuerza de rozamiento, por lo que oscilaría de lado a lado.
- Atractor caótico: Aparece en sistemas no lineales que tienen una gran sensibilidad a las condiciones. Un famoso ejemplo de estos atractores es el atractor de Lorenz.
Estos nombres se relacionan exactamente con el tipo de movimiento que provocan en los sistemas. Un atractor periódico, por ejemplo, puede guiar el movimiento de un péndulo en oscilaciones periódicas; sin embargo, el péndulo seguirá trayectorias erráticas alrededor de estas oscilaciones debidas a otros factores menores no considerados.
Ejemplos de atractores
editarSe verá una introducción de estos distintos tipos de atractores con un modelo matemático muy usado para explicar el caos. Consiste en una varilla de acero con un extremo fijado a un soporte y el otro libre para oscilar entre dos imanes colocados simétricamente. El soporte de la varilla se halla sometido a una fuerza armónica , como se observa en la figura del modelo matemático.
Es fácilmente observable que cuando la varilla está en posición vertical, hay un punto de equilibrio inestable entre dos puntos de equilibrio estables situados simétricamente. El potencial de este sistema es
de modo que la ecuación de movimiento será,
Si ahora se agrega una fuerza de rozamiento del aire proporcional a la velocidad (- ) y una fuerza externa armónica, se logra la ecuación de Duffing:
A continuación se ve cómo el término no lineal tiene consecuencias dinámicas asombrosas.
Suponiendo que inicialmente no se tiene fricción ( ) ni fuerza externa ( ), el sistema es conservativo y se tendrá una integral primera que proporciona las trayectorias en el espacio de fases :
En los mínimos de la energía potencial se observa que los puntos son estables mientras que el máximo corresponde a un punto de silla inestable. Las trayectorias de energía nula son órbitas homoclínicas que se hallan tanto en la variedad estable como en la inestable. Las demás trayectorias corresponden a oscilaciones periódicas cuyas órbitas encierran un solo punto estable ( ) o ambos ( ).
Si ahora se tiene en cuenta el rozamiento, se obtendrán oscilaciones amortiguadas, por lo que es lógico pensar que el sistema perderá energía monótonamente, mientras el tiempo transcurra. En consecuencia, las trayectorias tenderán a uno de los atractores de punto fijo.
Si ahora, además del rozamiento, se introduce una fuerza externa armónica que contrarresta a la fuerza de rozamiento, el sistema ya no tenderá al equilibrio. Al ser una fuerza armónica se encuentran soluciones periódicas (ciclos límite), pero nada que ver con los periodos de los que se habla cuando el sistema es conservativo ( ). En este caso los periodos son independientes de la energía por la fuerza de rozamiento y la armónica, así que los periodos dependen de la fuerza armónica externa.
Al aumentar la fuerza externa ( ), las órbitas periódicas desaparecen y oscilan sin cesar sin ninguna regularidad. Además de la irregularidad del sistema, este exhibe una gran sensibilidad a las condiciones iniciales por lo que nos encontramos ante un atractor extraño (o caótico).
En conclusión, para que haya caos en dimensión finita se necesita que se cumplan los siguientes 3 puntos en un sistema:
- El sistema debe ser no lineal.
- El sistema debe tener mínimo 3 variables (puede ser por ejemplo de 2 variables y no autónomo).
- El sistema debe tener dependencia sensible a las condiciones iniciales.
Cuando el modelo matemático tenía era un sistema no lineal, pero al introducir se logra la tercera variable, el tiempo. Aunque no tenía dependencia a las condiciones iniciales. Por eso se ha de remarcar que el caos implica que el sistema sea de 3 o más variables, pero 3 o más variables no implican que haya caos.
Una manera de visualizar el movimiento caótico, o cualquier tipo de movimiento, es hacer un diagrama de fases del movimiento. En tal diagrama el tiempo está implícito y cada eje representa una dimensión del estado. Por ejemplo, un sistema en reposo será dibujado como un punto, y un sistema en movimiento periódico será dibujado como un círculo.
Atractores extraños
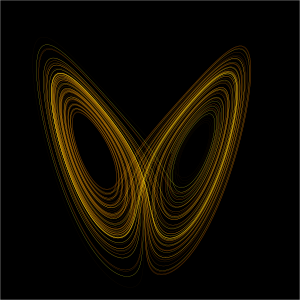
editarLa mayoría de los tipos de movimientos mencionados en la teoría anterior suceden alrededor de atractores muy simples, tales como puntos y curvas circulares llamadas ciclos límite. En cambio, el movimiento caótico está ligado a lo que se conoce como atractores extraños, que pueden llegar a tener una enorme complejidad como, por ejemplo, el modelo tridimensional del sistema climático de Lorenz, que lleva al famoso atractor de Lorenz. El atractor de Lorenz es, quizá, uno de los diagramas de sistemas caóticos más conocidos, no solo porque fue uno de los primeros, sino también porque es uno de los más complejos y peculiares, pues desenvuelve una forma particular, parecida a las alas de una mariposa.
Los atractores extraños están presentes tanto en los sistemas continuos dinámicos (tales como el sistema de Lorenz) como en algunos sistemas discretos (por ejemplo, la aplicación de Hénon). Otros sistemas dinámicos discretos tienen una estructura repelente, de tipo conjunto de Julia, la cual se forma en el límite entre las cuencas de dos puntos de atracción fijos. Julia puede ser sin embargo un atractor extraño. Ambos, atractores extraños y atractores tipo conjunto de Julia, tienen típicamente una estructura de fractal.
El teorema de Poincaré-Bendixson muestra que un atractor extraño solo puede presentarse como un sistema continuo dinámico si tiene tres o más dimensiones. Sin embargo, tal restricción no se aplica a los sistemas discretos, los cuales pueden exhibir atractores extraños en dos o incluso una dimensión.
Algo más de atractores
editarLos atractores extraños son curvas del espacio de fases que describen la trayectoria elíptica de un sistema en movimiento caótico. Un sistema con estas características es impredecible, conocer su configuración en un momento dado no permite predecirla con certeza en un momento posterior. De todos modos, el movimiento no es absolutamente aleatorio.
En la mayoría de sistemas dinámicos se encuentran elementos que permiten un tipo de movimiento repetitivo y, a veces, geométricamente establecido. Los atractores son los encargados de que las variables que inician en un punto de partida mantengan una trayectoria establecida, y lo que no se puede establecer de una manera precisa son las oscilaciones que las variables puedan tener al recorrer las órbitas que lleguen a establecer los atractores. Por ejemplo, es posible ver y de cierta manera prever la trayectoria de un satélite alrededor de la Tierra; lo que aparece, en este caso, como algo indeterminado son los movimientos e inconvenientes varios que se le pueden presentar al objeto para efectuar este recorrido.
Transformación del panadero
editarEn los atractores extraños se observan órbitas irregulares, que las trayectorias divergen exponencialmente y que permanecen en un espacio de fases acotado. Para explicar estas propiedades se usará la transformación del panadero que consiste en un doble proceso de estirar y plegar.
Este proceso doble de estirar (para separar exponencialmente las trayectorias) y plegar (para que la región del espacio de fases se mantenga acotado) es un mecanismo fundamental del caos determinista. A este proceso se le denomina transformación del panadero, porque el proceso de homogeneizar la masa consiste también en estirar (para homogeneizar) y plegar (para tener unas dimensiones manejables) la masa repetidas veces.
Al repetir infinitas veces el proceso, se logran infinitas capas que le dan al atractor una estructura fractal. Un ejemplo de esto se puede apreciar en el atractor de Rössler. Viendo el gráfico se observa cómo en el número 1 se estira y en el 3 se pliega. Cogiendo el 3 y volviendo a aplicar el proceso, se obtiene el doble de capas.
Otro ejemplo para explicar la trasformación es la ecuación de Duffing. En este caso como el espacio de fases es tridimensional. Pero al aparecer en un coseno, una dimensión es cíclica, por lo que para visualizar el atractor se considera una sección estroboscópica para valores , ( .
En el siguiente dibujo hay 16 secciones por lo que , ( )
Breve historia
editarEl caos y los fractales son parte de un tema más amplio, la dinámica, rama de la física que empezó a mediados de 1600 cuando Isaac Newton descubrió las ecuaciones diferenciales, las leyes de movimiento y la gravitación general. Con estos elementos Newton resolvió problemas de dos cuerpos que interactúan por medio de la gravedad pero, lo que de verdad le llamaba la atención era el movimiento de la Luna y su generalización conocida con el nombre de problema de los tres cuerpos. Las siguientes generaciones de matemáticos y físicos trataron problemas de tres cuerpos y notaron que resultaban mucho más difíciles que los problemas de dos cuerpos, hasta el punto de darlos como imposibles.
El determinismo laplaciano
editarEn 1776 el matemático francés Pierre Simon de Laplace comenzó a publicar los 5 volúmenes del Traité de Mécanique Céleste, donde el autor afirmaba categóricamente que, si se conociera la velocidad y la posición de todas las partículas del universo en un instante, se podría predecir su pasado y su futuro. Durante más de 100 años su afirmación pareció correcta y, por ello, se llegó a la conclusión de que el libre albedrío no tenía espacio en mecánica clásica, ya que todo estaba determinado por el estado del universo en un tiempo anterior.
El determinismo laplaciano consistía en afirmar que, si se conocen las leyes que gobiernan los fenómenos estudiados (y estas son deterministas como en mecánica clásica), se conocen las condiciones iniciales y se es capaz de calcular la solución, entonces se puede predecir con total certeza el futuro del sistema estudiado.
El cuestionamiento de Poincaré
editarA finales del siglo XIX Henri Poincaré (1854-1912), matemático francés, introdujo un nuevo punto de vista al preguntarse si el Sistema Solar sería estable para siempre. Poincaré fue el primero en pensar en la posibilidad del caos, en el sentido de un comportamiento que dependiera sensiblemente en las condiciones iniciales. En 1903 Poincaré postulaba acerca de lo aleatorio y del azar en los siguientes términos:
El azar no es más que la medida de la ignorancia del hombre.
reconociendo, a la vez, la existencia de innumerables fenómenos que no eran completamente aleatorios, sino que simplemente no respondían a una dinámica lineal; aquellos donde pequeños cambios en las condiciones iniciales conducían a enormes cambios en el resultado.
Algunas propiedades identificadas por Poincaré y que hacían imposible la predicción a largo plazo se encontraron en la práctica en sistemas físicos tales como el clima, la sangre fluyendo a través del corazón, las turbulencias, las formaciones geológicas, los atascos de vehículos, las epidemias, la bolsa y la forma en que las flores florecen en un prado.
El aporte de Lorenz
editarEl comienzo de la reciente historia del caos se sitúa en la década de 1950 cuando se inventaron los ordenadores y se desarrollaron algunas intuiciones sobre el comportamiento de los sistemas no lineales. Esto es, cuando se vieron las primeras gráficas sobre el comportamiento de estos sistemas mediante métodos numéricos. En 1963 Edward Lorenz trabajaba en unas ecuaciones, las mundialmente conocidas como ecuaciones de Lorenz, que esperaba predijeran el tiempo en la atmósfera, y trató mediante los ordenadores de ver gráficamente el comportamiento de sus ecuaciones. Los ordenadores de aquella época eran muy lentos, por eso se dice que Lorenz fue a tomar un té mientras el ordenador hacía los cálculos, y cuando volvió se encontró con una figura que ahora se conoce como atractor de Lorenz.
Pensó que se había cometido algún error al ejecutar el programa y lo intentó repetidas veces, logrando siempre el mismo resultado hasta que se dio cuenta de que algo pasaba con el sistema de ecuaciones simplificado con el que estaba trabajando. Después de estudiar detenidamente el problema y hacer pruebas con diferentes parámetros (tanto iniciales como las constantes del sistema), Lorenz llegó a la conclusión de que las simulaciones eran muy diferentes para condiciones iniciales muy próximas. Al llegar a la misma, recordó que en el programa que él había creado para su sistema de meteorología con la computadora u ordenador Royal McBee, se podían introducir un máximo de 3 decimales para las condiciones iniciales, aunque el programa trabajaba con 6 decimales y los 3 últimos decimales que faltaban se introducían aleatoriamente. Lorenz publicó sus descubrimientos en revistas de meteorología, pasando desapercibidos durante casi una década.
La década de 1970 fue el «auge del caos». En 1971 David Ruelle y Floris Takens propusieron una nueva teoría para la turbulencia de fluidos basada en un atractor extraño. Años después el ecólogo teórico Robert May en 1976 encontró ejemplos de caos en dinámica de poblaciones usando la ecuación logística discreta. A continuación llegó el más sorprendente descubrimiento de todos de la mano de Feigenbaum. Este descubrió que hay un conjunto de leyes universales concretas que diferencian la transición entre el comportamiento regular y el caos, por tanto, es posible que dos sistemas evolucionen hacia un comportamiento caótico semejante.
Ecuaciones de Lorenz
editarEl primer sistema de ecuaciones bien caracterizado que exhibía comportamiento caótico fue el sistema de ecuaciones propuesto por Lorenz:
donde es el número de Prandtl (viscosidad/conductividad térmica), es el número de Rayleigh (John Strutt) (diferencia de temperatura entre base y tope) y es la razón entre la longitud y altura del sistema.
Lorenz observó dos cosas fundamentales que ocurrían en su ecuación:
- Cualquier diferencia en las condiciones iniciales antes de los cálculos, incluso infinitesimal, cambiaba de forma drástica los resultados. Tan solo se podía predecir el sistema por cortos períodos. Llevando eso a la meteorología, suponía lo que se llamó efecto mariposa, hipersensibilidad a las condiciones iniciales.
- A pesar de lo anterior, la impredecibilidad del sistema, lejos de ser un comportamiento al azar, tenía una curiosa tendencia a evolucionar dentro de una zona muy concreta del espacio de fases, situando una especie de pseudocentro de gravedad de los comportamientos posibles.
Las ecuaciones de Lorenz fueron propuestas como un modelo muy simplificado de la convección en forma de anillos que parece ocurrir a veces en la atmósfera terrestre. Por ello, las tres magnitudes a las que Lorenz se refiere en su sistema son,
- Razón de rotación del anillo.
- Gradiente de temperatura.
- Desviación de la temperatura respecto a su valor de equilibrio.
Lorenz descubrió que su sistema contenía una dinámica extremadamente errática. Las soluciones oscilaban irregularmente sin llegar a repetirse, aunque lo hacían en una región acotada del espacio de fases. Vio que las trayectorias rondaban siempre alrededor de lo que ahora se define como atractor extraño. El sistema de Lorenz es disipativo.
Aplicaciones
editarLa teoría del caos y la teoría de sistemas dinámicos cuentan actualmente con numerosas aplicaciones tanto en ciencias naturales como en tecnología y ciencias sociales. Se han desarrollado aplicaciones prácticas en el campo del control, la caracterización y el modelado de sistemas complejos. Durante las cuatro décadas que siguieron a los años 1960 aumentó mucho la literatura sobre los sistemas complejos y la teoría del caos, así como las temáticas y aplicaciones alumbradas a raíz de la investigación en dicho campo interdisciplinar.
En Teoría del Caos, el tercer paradigma, se explica cómo la estadística inferencial trabaja con modelos aleatorios para crear series caóticas predictoras para el estudio de eventos presumiblemente caóticos en las ciencias sociales.
En meteorología
editarEl tiempo atmosférico, además de ser un sistema dinámico, es muy sensible a los cambios en las variables iniciales; es un sistema transitivo y también sus órbitas periódicas son densas, lo que hace del tiempo un sistema apropiado para trabajarlo con matemática caótica. La precisión de las predicciones meteorológicas es relativa, y los porcentajes anunciados tienen poco significado sin una descripción detallada de los criterios empleados para juzgar la exactitud de una predicción.
Al final del siglo XX se ha vuelto común atribuirles una precisión de entre 80 y 85 % en plazos de un día. Los modelos numéricos estudiados en la teoría del caos han introducido considerables mejoras en la exactitud de las previsiones meteorológicas en comparación con las predicciones anteriores, realizadas por medio de métodos subjetivos, en especial para periodos superiores a un día. Actualmente es posible demostrar la confiabilidad de las predicciones específicas para periodos de hasta cinco días gracias a la densidad entre las órbitas periódicas del sistema y se han logrado algunos éxitos en la predicción de variaciones anormales de la temperatura y la pluviosidad para periodos de hasta 30 días.
Antes de la aparición de la teoría del caos, se pensaba que para que el tiempo llegara a ser predicho con exactitud newtoniana no era más que una cuestión de introducir más y más variables en un ordenador lo suficientemente potente como para procesarlas. Sin embargo, de unas pocas variables de hace tan solo unas décadas se ha pasado a considerar cientos de miles de variables sin conseguir la predictibilidad esperada. El tiempo atmosférico, como sistema caótico, ha de entenderse como un sistema impredecible dentro de un atractor que le confiere cierto orden a través de las estaciones. Más recientemente se ha probado que el carácter caótico del tiempo atmosférico tiene que ver con las propiedades geométricas del grupo de evolución del sistema climático terrestre, en concreto dicho grupo puede dotarse de la estructura de una variedad de Riemann de dimensión infinita con curvatura negativa, lo cual implica que curvas arbitrariamente cercanas acaban divergiendo en el tiempo. Estos resultados sugieren una imposibilidad práctica de predecir el tiempo atmosférico a medio y largo plazo. Se ha estimado que una predicción a dos meses vista requeriría conocer las condiciones iniciales con una precisión unas 100 mil veces superior a la precisión obtenida por dicha predicción. El clima, por otra parte, al tratarse del tiempo atmosférico promedio no es tan sensible a las condiciones iniciales, lo que resulta en un sistema no caótico. En consecuencia, la capacidad de predicción del clima, a diferencia de la del tiempo, depende del conocimiento de todos los forzamientos radiativos que alteran el balance energético de la Tierra y no de una gran precisión en la medida de los valores iniciales.
En economía
editarEs posible que los modelos económicos también puedan mejorarse mediante la aplicación de la teoría del caos, pero predecir el estado de un sistema económico y qué factores influyen más en él es una tarea extremadamente compleja.[6] Según algunas interpretaciones, los sistemas económicos y financieros son fundamentalmente diferentes de los de las ciencias naturales clásicas, ya que los primeros son inherentemente de naturaleza estocástica, ya que resultan de las interacciones de las personas y, por lo tanto, es poco probable que los modelos deterministas puros proporcionen representaciones precisas. de los datos. La literatura empírica que prueba el caos en economía y finanzas presenta resultados muy variados, en parte debido a la confusión entre pruebas específicas para el caos y pruebas más generales para relaciones no lineales.[7]
El caos se puede encontrar en la economía por medio de recurrence quantification analysis (i.e. análisis de cuantificación de recurrencia). De hecho, Orlando et al.[8] por medio del llamado índice de correlación de cuantificación de recurrencia fueron capaces de detectar cambios ocultos en las series temporales. Luego, se empleó la misma técnica para detectar transiciones de fases laminares (regulares) a turbulentas (caóticas), así como diferencias entre variables macroeconómicas y resaltar características ocultas de la dinámica económica.[9] Finalmente, el caos podría ayudar a modelar el funcionamiento de la economía, así como a incorporar shocks debido a eventos externos como el COVID-19.[10]
En medicina
editarEl análisis de las series temporales procedentes de electrocardiogramas y encefalogramas que en algunos detalles presentan detalles aparentemente aleatorios, parecen estar generados por una dinámica que de hecho es un sistema caótico. Los exponentes y parámetros matemáticos que caracterizan dichas series han podido ser usados como medio de diagnóstico de ciertas patologías. Esto permite un diagnóstico precoz de algunas de esas patologías.
Véase también
editarReferencias
editar- ↑ Ivancevic, Vladimir G.; Tijana T. Ivancevic (2008). Complex nonlinearity: chaos, phase transitions, topology change, and path integrals. Springer. ISBN 978-3-540-79356-4.
- ↑ Mosko M.S., Damon F.H. (Eds.) (2005). On the order of chaos. Social anthropology and the science of chaos. Oxford: Berghahn Books.
- ↑ Piotrowski, Chris. «Covid-19 Pandemic and Chaos Theory: Applications based on a Bibliometric Analysis». researchgate.net. Consultado el 13 de mayo de 2020.
- ↑ Weinberger, David (2019). Everyday Chaos – Technology, Complexity and How We're Thriving in a New World of Possibility. Harvard Business Review Press. ISBN 9781633693968.
- ↑ «Análisis Computacional de Modelos Biológicos para su Aplicación a Modelos Económicos». CIT Internacional.
- ↑ Juárez, Fernando (2011). «Applying the theory of chaos and a complex model of health to establish relations among financial indicators». Procedia Computer Science 3: 982-986. doi:10.1016/j.procs.2010.12.161.
- ↑ Brooks, Chris (1998). «Chaos in foreign exchange markets: a sceptical view». Computational Economics 11 (3): 265-281. ISSN 1572-9974. S2CID 118329463. doi:10.1023/A:1008650024944. Archivado desde el original el 9 de agosto de 2017.
- ↑ Orlando, Giuseppe; Zimatore, Giovanna (18 de diciembre de 2017). «RQA correlations on real business cycles time series». Indian Academy of Sciences – Conference Series 1 (1): 35-41. doi:10.29195/iascs.01.01.0009.
- ↑ Orlando, Giuseppe; Zimatore, Giovanna (1 de mayo de 2018). «Recurrence quantification analysis of business cycles». Chaos, Solitons & Fractals (en inglés) 110: 82-94. Bibcode:2018CSF...110...82O. ISSN 0960-0779. S2CID 85526993. doi:10.1016/j.chaos.2018.02.032.
- ↑ Orlando, Giuseppe; Zimatore, Giovanna (1 de agosto de 2020). «Business cycle modeling between financial crises and black swans: Ornstein–Uhlenbeck stochastic process vs Kaldor deterministic chaotic model». Chaos: An Interdisciplinary Journal of Nonlinear Science 30 (8): 083129. Bibcode:2020Chaos..30h3129O. PMID 32872798. S2CID 235909725. doi:10.1063/5.0015916.
Bibliografía
editar- (en inglés) Kathleen T. Alligood, Tim Sauer et James A. Yorke, Chaos: An Introduction to Dynamical Systems, Springer-Verlag, 1997 ISBN 978-0-387-94677-1
- (en inglés) Vladimir Arnold, Mathematical Methods of Classical Mechanics, Springer-Verlag, 2×10{{{1}}} édition, 1989 ISBN 0-387-96890-3.
- (en inglés) Vladimir Arnold, V.V. Kozlov et A.I. Neishtadt, Mathematical Aspects of Classical and Celestial Mechanics, Encyclopaedia of Mathematical Sciences, Springer-Verlag (2×10{{{1}}} édition-1993). Une synthèse de l'état de l'art en mécanique céleste, par l'un des plus brillants mathématiciens du domaine (Arnold) et ses collaborateurs. À partir du second cycle universitaire.
- (en inglés) Vladimir Arnold y André Avez, Ergodic problems of classical mechanics, Advanced Book Classics, Addison-Wesley, 1988.
- (en inglés) Vladimir Damgov, Nonlinear and parametric phenomena - Applications in radiophysical and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.
- González-Miranda, J. M. (2004). Synchronization and Control of Chaos. An introduction for scientists and engineers. Imperial College Press. ISBN 1-86094-488-4.
- Gutzwiller, Martin (1990). Chaos in Classical and Quantum Mechanics. Springer-Verlag New York, LLC. ISBN 0-387-97173-4.
- (en inglés) Robert May, Simple Mathematical Models with Very Complicated Dynamics, Nature, Vol. 261, p. 459, 10 de junio de 1976.
- Moon, Francis (1990). Chaotic and Fractal Dynamics. Springer-Verlag New York, LLC. ISBN 0-471-54571-6.
- Perpinyà, Núria (2021). Caos, virus, calma. La Teoría del Caos aplicada al desórden artístico, social y político. Páginas de Espuma. ISBN 978-84-8393-288-9
- Orlando G., Pisarchik A., Stoop R. (2021). Nonlinearities in Economics: An Interdisciplinary Approach to Economic Dynamics, Growth and Cycles. Springer-Verlag. doi:10.1007/978-3-030-70982-2.
- Ott, Edward (2002). Chaos in Dynamical Systems. Cambridge University Press New, York. ISBN 0-521-01084-5.
- (en francés) Henri Poincaré, Les méthodes nouvelles de la mécanique céleste, 3 volumes, Éditions Gauthiers-Villars, 1892
- (en francés) Jacques Hadamard, Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de mathématiques pures et appliquées 4 (1898), 27. Pour une revue plus récente, voir e.g. la référence suivante : Pierre Pansu, Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991) publié dans : Astérisque 201-203 (1991) 269-298.
- Hoover, William Graham (1999,2001). Time Reversibility, Computer Simulation, and Chaos. World Scientific. ISBN 981-02-4073-2.
- (en inglés) T. W. B. Kibble et F.H. Berkshire, Classical Mechanics, Prentice Hall, 4×10{{{1}}} édition, 1997 ISBN 0-582-25972-X.
- (en inglés) David Ruelle, Deterministic chaos: the science and the fiction, Proceedings of the Royal Society London A 427 (1990), 241-248
- (en inglés) David Ruelle et Jean-Pierre Eckman, Ergodic theory of chaos and strange attractors, Review of Modern Physisc 57 (1985), 617-656
- Solé, R. V., y Manrubia, S. C. (2001). Orden y caos en sistemas complejos. Universidad Politécnica de Cataluña, ISBN 9788483014301
- Santos-Burguete, Carlos (2018). Física del caos en la predicción meteorológica. ed. digital de libre distribución NIPO: 014-18-009-X (1ª edición). AEMET. p. 1156. Consultado el 11 de noviembre de 2018.
Enlaces externos
editar- Wikimedia Commons alberga una categoría multimedia sobre Teoría del caos.
- Artículo divulgativo sobre el creciente aporte de la Teoría del Caos en Medicina Servicio de divulgación científica DivulgaUNED (Universidad Nacional de Educación a Distancia de España, octubre de 2009).
- Alcances y limitaciones de la Teoría del Caos aplicada al análisis del Comportamiento Organizacional, Cultural y la necesidad del cambio De la Universidad Peruana de Ciencias Aplicadas
- Fundamentos matemáticos de la sinergética. Caos, estructuras y simulación por ordenador
- Modelado y Simulación de un Oscilador Caótico usando MatLab Archivado el 17 de noviembre de 2016 en Wayback Machine.