Teorema de Ptolomeo
El teorema de Ptolomeo es una relación en geometría euclidiana entre los cuatro lados y las dos diagonales de un cuadrilátero cíclico. El teorema recibe su nombre del astrónomo y matemático griego Claudio Ptolomeo.
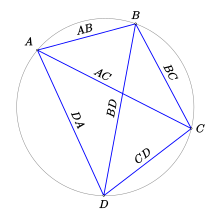
Si un cuadrilátero está dado por sus cuatro vértices A, B, C, D, el teorema afirma que:
Esta relación puede ser expresada de manera verbal de la siguiente forma:
|
Demostraciones
editarDemostración geométrica
editar- Sea ABCD un cuadrilátero cíclico.
- Note que en el segmento BC, ángulos inscritos ∠BAC = ∠BDC, y en AB, ∠ADB = ∠ACB.
- Ahora, por ángulos comunes △ABK es semejante a △DBC, y △ABD ∼ △KBC
- Por lo tanto AK/AB = CD/BD, y CK/BC = DA/BD,
- Por lo tanto AK·BD = AB·CD, y CK·BD = BC·DA;
- Lo que implica AK·BD + CK·BD = AB·CD +BC·DA
- Es decir, (AK+CK)·BD = AB·CD + BC·DA;
- Pero AK+CK = AC, por lo tanto AC·BD = AB·CD + BC·DA; como se quería demostrar.
Note que la demostración es válida solo para cuadriláteros concíclicos simples. Si el cuadrilátero es complejo entonces K se encontrará fuera del segmento AC, y por lo tanto AK-CK=±AC, tal como se esperaba.
Existe una generalización de este teorema llamado el teorema de Casey, que involucra a cuatro circunferencias no secantes y tangentes interiores a una quinta.
El teorema de Ptolomeo se puede demostrar con métodos de inversión geométrica con respecto a cualquier vértice de un cuadrilátero.[1]
Ejemplo
editarConsidérese un pentágono regular y la circunferencia circunscrita al mismo. En el cuadrilátero ABCD las diagonales son iguales al lado AD. El teorema de Ptolomeo arroja en este caso,
Dividiendo entre se tiene
Denotando con la razón b/a se obtiene , ecuación que coinicide con la definición del número áureo.
- .
Referencias
editar- ↑ Adam Puig Curso de Geometría Métrica, Tomo 1 ISBN 84-85731-03-4.
Enlaces externos
editar- Teorema de Ptolomeo en PlanetMath
- Weisstein, Eric W. «Desigualdad de Ptolomeo». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
