Teorema japonés para polígonos cíclicos
|
|
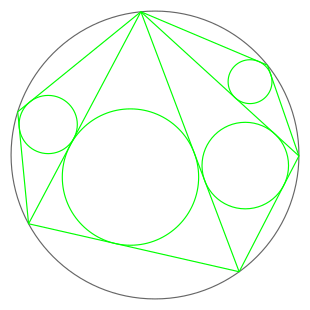
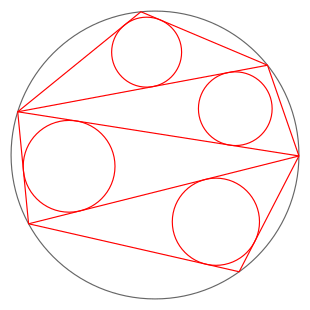
| Suma de los radios de los círculos verdes = Suma de los radios de los círculos rojos | |
En geometría, el teorema japonés establece que independientemente de cómo se triangule un polígono cíclico, la suma de los inradios de los triángulos es constante.[1] : p. 193
Recíprocamente, si la suma de los inradios es independiente de la triangulación, entonces el polígono es cíclico. El teorema japonés se deduce del teorema de Carnot, y forma parte de los problemas de Sangaku.
Demostración
editarEste teorema se puede demostrar comprobando primero un caso especial: no importa cómo se triangule un cuadrilátero cíclico, la suma de los inradios de los triángulos es constante.
Después de probar el caso del cuadrilátero, el caso general del teorema del polígono cíclico es un corolario inmediato. La regla del cuadrilátero se puede aplicar a los componentes del cuadrilátero de una partición general de un polígono cíclico, y la aplicación repetida de la regla, que "da la vuelta" a una diagonal, generará todas las particiones posibles con respecto a cualquier partición dada, preservando la suma de los inradios con cada "volteo".
El caso del cuadrilátero se deriva de una extensión simple del teorema japonés para los cuadriláteros cíclicos, que demuestra que los dos pares de incentros correspondientes a las dos posibles triangulaciones de un cuadrilátero cíclico forman un rectángulo. Los pasos de este teorema no requieren nada más que geometría constructiva euclídea básica.[2]
Con la construcción adicional de un paralelogramo que tiene sus lados paralelos a las diagonales y tangentes a las esquinas del rectángulo formado por los incentros, el caso del cuadrilátero correspondiente al teorema del polígono cíclico se puede probar en unos pocos pasos. La igualdad de las sumas de los radios de los dos pares de circunferencias inscritas es equivalente a la condición de que el paralelogramo construido sea un rombo, y esto se muestra fácilmente en la construcción.
Otra prueba del caso del cuadrilátero debida a Wilfred Reyes (2002) está disponible en línea.[3] En esta demostración del teorema japonés para cuadriláteros cíclicos y para polígonos cíclicos, se parte del problema III relativo al teorema de Thébault.
Véase también
editar- Teorema de Carnot, que se utiliza en una prueba del teorema anterior
- Teorema de los incírculos iguales
- Líneas tangentes a circunferencias
Referencias
editar- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- ↑ Fukagawa, Hidetoshi; Pedoe, D. (1989). Japanese Temple Geometry. Manitoba, Canada: Charles Babbage Research Center. pp. 125-128. ISBN 0919611214.
- ↑ Reyes, Wilfred (2002). «An Application of Thébault's Theorem». Forum Geometricorum 2: 183-185. Consultado el 2 de septiembre de 2015.
Bibliografía
editar- Claudi Alsina, Roger B. Nelsen: Icons of Mathematics: An Exploration of Twenty Key Images. MAA, 2011, ISBN 9780883853528, pp. 121-125
- Wilfred Reyes: An Application of Thebault’s Theorem. Forum Geometricorum, Volume 2, 2002, pp. 183–185
Enlaces externos
editar- Mangho Ahuja, Wataru Uegaki, Kayo Matsushita: In Search of the Japanese Theorem
- Japanese theorem at Mathworld
- Japanese Theorem interactive demonstration at the C.a.R. website
- Wataru Uegaki: "Japanese Theoremの起源と歴史" (On the Origin and History of the Japanese Theorem) http://hdl.handle.net/10076/4917