Test de Chow

El test de Chow, es un test estadístico y econométrico que prueba si los coeficientes en dos regresiones lineales en dos sets de datos son iguales. El test de Chow fue inventado por el economista Gregory Chow Masgow. En econometría, el test de Chow es normalmente usado en el análisis de series de tiempo para probar la presencia de un cambio estructural.

En $x=1.7$ hay un cambio estructura, las regresiones en los intervalos $(0,1.7)$ y $(1.7,4)$ generan mejores modelos que la regresión combinada(línea punteada) en todo el intervalo.

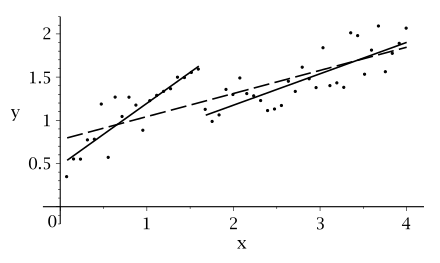
Supongamos que el modelo utilizado para un determinado conjunto de datos es:

$y_{t}=a+bx_{1t}+cx_{2t}+\varepsilon .\,$

Si dividimos el conjunto en dos grupos, entonces tendremos

$y_{t}=a_{1}+b_{1}x_{1t}+c_{1}x_{2t}+\varepsilon .\,$

y

$y_{t}=a_{2}+b_{2}x_{1t}+c_{2}x_{2t}+\varepsilon .\,$

La hipótesis nula del test de Chow será que $a_{1}=a_{2}$, $b_{1}=b_{2}$, y $c_{1}=c_{2}$.

Sea $S_{C}$ la suma de cuadrados residuos de la serie original, $S_{1}$ la suma de cuadrados residuos del primer grupo y $S_{2}$ la suma de cuadrados residuos del segundo grupo.$N_{1}$ y $N_{2}$ son el número de observaciones en cada grupo y $k$ es el número total de parámetros (en este caso, 3). Entonces el estadístico del test de Chow será

${\frac {(S_{C}-(S_{1}+S_{2}))/(k)}{(S_{1}+S_{2})/(N_{1}+N_{2}-2k)}}.$

El estadístico del test se comporta como una distribución F con $k$ y $N_{1}+N_{2}-2k$ grados de libertad.

Referencias

• Howard E. Doran: Applied Regression Analysis in LOSER Econometrics. CRC Press 1989, ISBN 0-8247-8049-3, p. 146 (restricted online version (Google Books))
• Christopher Dougherty: Introduction to Econometrics. Oxford University Press 2007, ISBN 0-19-928096-7, p. 194 (restricted online version (Google Books))
• Gregory C. Chow (1960). «Tests of Equality Between Sets of Coefficients in Two Linear Regressions». Econometrica 28 (3): 591-605. JSTOR 1910133. doi:10.2307/1910133. 
• [1] [2] [3] Series of explanations from the Stata Corporation

• Datos: Q1076792
• Multimedia: Chow test / Q1076792