Triángulo de Penrose
El triángulo de Penrose es un objeto imposible que fue creado en 1934 por el artista sueco Oscar Reutersvärd. Posteriormente fue redescubierto de forma independiente por el físico Roger Penrose, en la década de los 1950, quien lo hizo popular, describiéndolo como "imposibilidad en su forma más pura".[1] Aparece de forma destacada en las obras del artista M. C. Escher, hasta el punto que fue parcialmente inspirado por sus primeras imágenes de objetos imposibles. El término puede referirse tanto al objeto imposible como a su representación bidimensional.
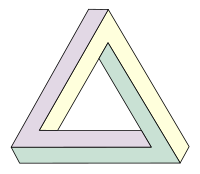
Este objeto imposible aparenta ser un objeto sólido, formado por tres tramos rectos de sección cuadrada, que se encuentran unidos formando ángulos rectos en los extremos del triángulo que conforman. Esta combinación de propiedades no puede ser satisfecha por ninguna figura tridimensional en un espacio euclídeo ordinario. En cambio, en ciertas 3-variedades sí que pueden existir.[2]
Existen además objetos tridimensionales sólidos que, cuando son observados desde el ángulo apropiado, aparentan ser triángulos de Penrose.
La litografía de M.C. Escher Cascada representa una corriente de agua que fluye en zigzag a lo largo de los lados de dos triángulos de Penrose alargados, de tal forma que acaba dos pisos más arriba de donde comienza. La catarata resultante, formada en los lados cortos de ambos triángulos, hace funcionar una noria. Escher puntualiza que para poder mantener la noria funcionando, es necesario agregar de vez en cuando algo de agua, para compensar las pérdidas por evaporación.
Si se traza una línea en torno al triángulo de Penrose, se forma una banda de Möbius de 3 vueltas.
Otros polígonos de Penrose
editarEs posible construir un triángulo de Penrose con otros polígonos regulares, creando así un polígono de Penrose, aunque el efecto visual no es tan impactante, ya que al incrementarse el número de lados, la imagen parece distorsionada o retorcida.
Referencias
editar- ↑ J. Robinson (1998), The Psychology of Visual Illusion, Dover, Nueva York. ISBN 0-486-40449-8.
- ↑ Francis, George (1988). A topological picturebook. Springer. ISBN 0387964266. In the chapter on the Penrose tribar, Francis attributes this observation to John Stillwell.
Enlaces externos
editar
Wikimedia Commons alberga una categoría multimedia sobre Triángulos de Penrose.- Wikimedia Commons alberga una galería multimedia sobre Triángulo de Penrose.
- A family of impossible figures studied by knot theory (Idioma inglés)
- Escher for Real constructions (Idioma inglés)
Datos: Q12141- Multimedia: Penrose triangles / Q12141
