Usuario:Raulshc/Glosario de teoría de grafos
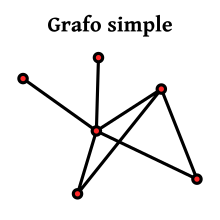
A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los ejemplos están basados en la imagen de la derecha.
A
editar
Adyacenteseditar
| |
Árboleditar
| |
Arcoeditar
| |
Aristaeditar
|
B
editar
Bosqueeditar
| |
Bucleeditar | |
Búsqueda en anchuraeditar
| |
Búsqueda en profundidadeditar
|
C
editar
Caminoeditar
| |
Camino eulerianoeditar
| |
Camino hamiltonianoeditar
| |
Cicloeditar
| |
Ciclo eulerianoeditar
| |
Ciclo hamiltonianoeditar
| |
Circunferenciaeditar
| |
Cliqueeditar
| |
Cobertura de vérticeseditar
| |
Coloración de grafoseditar
| |
Contracción (de aristas)editar
| |
Componente fuertemente conexoeditar
| |
Conjunto estableeditar
| |
Conjunto independienteeditar
| |
Coveringeditar
|
D
editarDepth First Search
editar- Véase Búsqueda en profundidad.
DFS
editar- Véase Búsqueda en profundidad.
Digrafo
editar- Es un grafo cuyas aristas son dirigidas, es decir, cada arista posee un vértice inicial y uno final.
Distancia
editarE
editarEuleriano
editar- Véase Ciclo euleriano.
G
editarGirth
editar- El girth o cintura de un grafo es la longitud del ciclo simple más corto en el grafo. El "girth" de un grafo acíclico se define como infinito.
Grado
editar- El grado o valencia de un vértice es el número de aristas incidentes en él. Para un grafo con bucles, estos son contados por dos. En el ejemplo, los vértices 1 y 3 tienen grado 2; los vértices 2, 4 y 5, grado 3; y el vértice 6, grado 1.
- En un digrafo, podemos distinguir el grado saliente (el número de aristas que dejan el vértice) y el grado entrante (el número de aristas que entran en un vértice). El grado de un vértice sería la suma de ambos números.
Grafo
editarGrafo acíclico
editar- Un grafo se dice acíclico si no contiene ningún ciclo simple.
Grafo bipartito
editar- Un grafo bipartito es cualquier grafo cuyos vértices pueden ser divididos en dos conjuntos, tal que no haya aristas entre los vértices del mismo conjunto. Se ve que un grafo es bipartito si no hay ciclos de longitud impar. Véase también grafo bipartito completo.
- Un grafo k-partido o grafo k-colorable es un grafo con cuyos vértices se puede hacer una partición en k subconjuntos disjuntos tal que no haya aristas entre vértices del mismo subconjunto. Un grafo 2-partido es lo mismo que un grafo bipartito.
- Un grafo k-partido se dice semiregular si cada partición tiene un grado uniforme.
Grafo completo
editar- Un grafo completo es un grafo simple en el que cada vértice es adyacente a cualquier otro vértice. El del ejemplo no es completo. El grafo completo en n vértices se denota a menudo por Kn. Tiene n(n-1)/2 aristas (correspondiendo a todas las posibles elecciones de pares de vértices).
Grafo conexo
editar- Si es posible formar un camino desde cualquier vértice a cualquier otro en el grafo, decimos que el grafo es conexo. Si es posible hacer esto incluso tras quitar k-1 vértices, decimos que el grafo es k-conexo.
- Un grafo es k-conexo si y sólo si contiene k caminos independientes entre cualesquiera dos vértices. Teorema de Menger El grafo ejemplo es conexo (y por tanto 1-conexo), pero no es 2-conexo.
Grafo denso
editar- Un grafo denso es un grafo en el que el número de aristas está cercano al número de máximo de aristas. Lo opuesto, un grafo con solo algunas aristas, es un grafo disperso.
Grafo dirigido
editar- Es un conjunto de vértices V y un conjunto de aristas E tal que para cada arista perteneciente al conjunto de aristas E se asocia con dos vértices en forma ordenada.
- Véase Digrafo.
Grafo nulo
editar- El grafo nulo es el grafo cuyos conjuntos de aristas y de vértices son vacíos.
Grafo plano
editar- Un grafo plano es uno que es posible dibujar en el plano sin que ningún par de aristas se interseque. El del ejemplo lo es; el grafo completo de n vértices, para n > 4, no es plano.
Grafo ponderado
editar- Un grafo ponderado asocia un valor o peso a cada arista en el grafo. El peso de un camino en un grafo con pesos es la suma de los pesos de todas las aristas atravesadas.
Grafo regular
editar- Un grafo regular es un grafo cuyos vértices tienen todos el mismo grado.
Grafo simple
editar- Un grafo simple es un grafo o digrafo que no tiene bucles, y que no es un multigrafo.
Grafo trivial
editar- Un grafo trivial es un grafo vacío con un único vértice.
Grafo universal
editar- Un grafo universal en una clase K de grafos es un grafo en el que puede incluirse como subgrafo todo elemento de K.
Grafo vacío
editar- Un grafo vacío es el grafo cuyo conjunto de aristas es vacío.
H
editarHamiltoniano
editar- Véase Camino hamiltoniano.
Hipergrafo
editar- Un hipergrafo es una generalización de un grafo, cuyas aristas aquí se llaman hiperaristas, y pueden relacionar a cualquier cantidad de vértices, en lugar de sólo un máximo de dos como en el caso particular.
I
editarIncidencia
editar- Véase Vecindad.
Isomorfismo
editar- Un Isomorfismo de grafos entre dos grafos G y H es una biyección f entre los conjuntos de sus vértices que preserva la relación de adyacencia. Es decir, cualquier par de vértices u y v de G son adyacentes si y solo si lo son sus imágenes, f(u) y f(v), en H.
L
editarLista de adyacencia
editar- Una lista de adyacencia es una representación de todas las aristas o arcos de un grafo mediante una lista.
Lista de grados
editarLoop
editar- Véase Bucle.
M
editarMatriz de adyacencia
editar- Una matriz de adyacencia es una matriz de n x n que permite representar un grafo o digrafo finito, donde cada valor en la posición (i, j) representa el número de aristas desde el vértice i-ésimo al j-ésimo.
N
editarNodo
editar- Véase Vértice.
Número cromático
editar- El número cromático es el mínimo de colores necesarios para colorear los vértices de un grafo. El número cromático de un grafo es .
O
editarOrden
editar- Se llama orden del grafo a su número de vértices, designado como .
P
editarPuente
editar- Un puente a es una arista tal que si la quitamos nos quedamos con un grafo con una componente conexa más que el original.
Punto de articulación
editar- Véase Vértice de corte.
Punto de corte
editar- Véase Vértice de corte.
R
editarRecubrimiento de vértices
editar- Véase Cobertura de vértices.
S
editarSubárbol
editar- Un subárbol de un grafo G es un subgrafo que es además un árbol.
Subgrafo
editar- Un subgrafo de un grafo G es un grafo cuyo conjunto de vértices es un subconjunto del de G, cuyo conjunto de aristas es un subconjunto del conjunto de las aristas de G, y tal que la aplicación w es la restricción de la aplicación de G.
Subgrafo de expansión
editar- Un subgrafo de expansión de un grafo G es un subgrafo con el mismo conjunto de vértices que G. Un árbol expansión es un subgrafo expansión que es un árbol. Cada grafo tiene un árbol de expansión.
T
editarTeoría espectral
editar- La teoría espectral es aquella que estudia las relaciones entre las propiedades de la matriz de adyacencia y las de su grafo.
Torneo
editar- Un torneo es un grafo dirigido completo, simple, no generalizado, no degenerado y sin dígonos.
V
editarValencia
editar- Véase Grado.
Vecindad
editar- Dos vértices son vecinos, adyacentes o incidentes si existe una arista entre ellos. En el ejemplo, el vértice 1 tiene dos vecinos: el vértice 2 y el 5. Para un grafo simple, el número de vecinos de un vértice es igual a su grado.
Vértice
editarVértice de corte
editar- Un vértice de corte es un vértice tal que si lo quitamos nos quedamos con un grafo con más componentes conexas que el original.
