Varianza de Allan
La varianza de Allan (abreviadamente en inglés, AVAR,), también conocida como varianza de dos muestras, es una medida de estabilidad de la frecuencia en relojes, osciladores y amplificadores. Lleva el nombre de David W. Allan y se expresa matemáticamente como .

La desviación de Allan (abreviado en inglés, ADEV), también conocida como sigma-tau, es la raíz cuadrada de la varianza de Allan, .
La varianza de M muestras es una medida de la estabilidad de la frecuencia utilizando M muestras, el tiempo T entre las mediciones y el tiempo de observación . La varianza de M muestras se expresa como
La varianza de Allan tiene por objeto estimar la estabilidad debida a los procesos de ruido y no la de los errores sistemáticos o las imperfecciones, como la deriva de la frecuencia o los efectos de la temperatura. La varianza Allan y la desviación Allan describen la estabilidad de la frecuencia. Véase también el apartado Interpretación del valor más abajo.
También existen diferentes adaptaciones o alteraciones de la varianza de Allan, especialmente la varianza de Allan modificada MAVAR o MVAR, la varianza total y la varianza de Hadamard. También existen variantes de la estabilidad temporal, como la desviación temporal (TDEV) o la varianza temporal (TVAR). La varianza de Allan y sus variantes han demostrado su utilidad fuera del ámbito de la medición del tiempo y son un conjunto de herramientas estadísticas mejoradas que se utilizan siempre que los procesos de ruido no son incondicionalmente estables, por lo que existe una derivada.
La varianza general de M muestras sigue siendo importante, ya que permite determinar el tiempo muerto (el tiempo después de cada evento durante el cual el sistema no puede registrar otro evento en las mediciones), y las funciones de sesgo permiten la conversión en valores de varianza de Allan. Sin embargo, para la mayoría de las aplicaciones, el caso especial de 2 muestras, o "varianza de Allan" con es el de mayor interés.
Antecedentes
editarAl investigar la estabilidad de los osciladores de cristal y los relojes atómicos, se descubrió que no tenían un ruido de fase compuesto únicamente por ruido blanco, sino también por ruido de frecuencia de parpadeo. Estas formas de ruido se convierten en un reto para las herramientas estadísticas tradicionales, como la desviación estándar, ya que el estimador no converge. Por tanto, se dice que el ruido es divergente. Los primeros esfuerzos por analizar la estabilidad incluyeron tanto análisis teóricos como mediciones prácticas.[1][2]
Una importante consecuencia colateral de contar con estos tipos de ruido era que, al no coincidir los distintos métodos de medición entre sí, no se podía conseguir el aspecto clave de la repetibilidad de una medición. Esto limita la posibilidad de comparar fuentes y hacer especificaciones significativas para exigir a los proveedores. Esencialmente, todas las formas de uso científico y comercial se limitaron entonces a mediciones dedicadas, que se espera que capten la necesidad de esa aplicación.
Para abordar estos problemas David Allan introdujo la varianza de M muestras e (indirectamente) la varianza de dos muestras.[3] Aunque la varianza de dos muestras no permitía distinguir completamente todos los tipos de ruido, proporcionaba un medio para separar de forma significativa muchas formas de ruido para las series temporales de mediciones de fase o frecuencia entre dos o más osciladores. Allan proporcionó un método para convertir cualquier varianza de M muestras en cualquier varianza de N muestras a través de la varianza común de dos muestras, haciendo así comparables todas las varianzas de M muestras. El mecanismo de conversión también demostró que la varianza de M muestras no converge para valores grandes de M, lo que las hace menos útiles. El IEEE identificó posteriormente la varianza de 2 muestras como la medida preferida.[4]
Una de las primeras preocupaciones estaba relacionada con los instrumentos de medición de tiempo y frecuencia que tenían un tiempo muerto entre las mediciones. Estas series de mediciones no formaban una observación continua de la señal y, por tanto, introducían un sesgo sistemático en la medición. Se puso mucho cuidado en la estimación de estos sesgos. La introducción de los contadores de tiempo muerto cero eliminó esta necesidad, pero las herramientas de análisis de los sesgos han resultado útiles.
Otro aspecto que preocupaba al principio estaba relacionado con la forma en que el ancho de banda del instrumento de medición influiría en la medición, de manera que era necesario tomar nota. Más tarde se comprobó que cambiando algorítmicamente la observación sólo los valores bajos de se verían afectados, mientras que los valores más altos no lo harían. El cambio de se hace dejando que sea un múltiplo entero de la base de tiempo de medición :
La física de los osciladores de cristal fue analizada por D. B. Leeson,[2] y el resultado se conoce ahora como ecuación de Leeson. La retroalimentación en el oscilador hará que el ruido blanco y el ruido de parpadeo del amplificador de retroalimentación y del cristal se conviertan en los ruidos de color de frecuencia de ruido blanco y de frecuencia de ruido de parpadeo respectivamente. Estas formas de ruido tienen el efecto de que el estimador de varianza estándar no converge al procesar las muestras de error temporal. Esta mecánica de los osciladores de retroalimentación era desconocida cuando se iniciaron los trabajos sobre la estabilidad de los osciladores, pero fue presentada por Leeson al mismo tiempo que el conjunto de herramientas estadísticas fue puesto a disposición por David W. Allan. Para una presentación más completa del efecto Leeson, véase la literatura moderna sobre el ruido de fase.[5]
Interpretación del valor
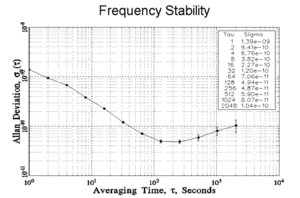
editarLa varianza de Allan se define como la mitad de la media temporal de los cuadrados de las diferencias entre las lecturas sucesivas de la desviación de la frecuencia muestreada a lo largo del periodo de muestreo. La varianza de Allan depende del período de tiempo utilizado entre las muestras, por lo tanto, es una función del período de muestreo, comúnmente denotado como , al igual que la distribución que se está midiendo, y se muestra como un gráfico en lugar de un solo número. Una varianza Allan baja es una característica de un reloj con buena estabilidad a lo largo del periodo medido.
La desviación de Allan se utiliza ampliamente para las gráficas (convencionalmente en formato log-log) y la presentación de los números. Se prefiere, ya que da la estabilidad de la amplitud relativa, lo que permite una fácil comparación con otras fuentes de error.
Una desviación de Allan de 1,3×10-9 en un tiempo de observación de 1 s (es decir, = 1 s) debe interpretarse como la existencia de una inestabilidad en la frecuencia entre dos observaciones separadas por 1 segundo con un valor medio cuadrático relativo (RMS) de 1,3×10-9. Para un reloj de 10 MHz, esto equivaldría a un movimiento RMS de 13 mHz. Si se necesita la estabilidad de fase de un oscilador, hay que consultar y utilizar las variantes de desviación temporal.
Se puede convertir la varianza de Allan y otras varianzas del dominio del tiempo en medidas del dominio de la frecuencia de la estabilidad del tiempo (fase) y de la frecuencia.[6]
Definiciones
editarVarianza de M muestras
editarLa varianza de M muestras se define[3] (aquí en una forma de notación modernizada) como
donde es la lectura del reloj (en segundos) medida en el momento , o con la serie temporal de frecuencia media fraccionaria
donde es el número de muestras de frecuencia utilizadas en la varianza, es el tiempo entre cada muestra de frecuencia, y es la duración de cada estimación de frecuencia.
Un aspecto importante es que la varianza de muestras puede incluir el tiempo muerto dejando que el tiempo sea diferente al de .
Varianza de Allan
editarLa varianza de Allan se define como
donde denota valor esperado. Esto se puede expresar convenientemente como
donde es el período de observación, e es la enésima frecuencia fraccionaria media a lo largo del tiempo de observación .
Las muestras se toman sin tiempo muerto entre ellas, lo que se consigue dejando
Desviación de Allan
editarAl igual que la desviación estándar y la varianza, la desviación de Allan se define como la raíz cuadrada de la varianza de Allan:
Definiciones de apoyo
editarModelo de oscilador
editarSe supone que el oscilador analizado sigue el modelo básico de
Se supone que el oscilador tiene una frecuencia nominal de dada en ciclos por segundo (unidad del SI: hertz). La frecuencia angular nominal (en radianes por segundo) viene dada por
La fase total puede separarse en un componente perfectamente cíclico junto con un componente fluctuante :
Error temporal
editarLa función de error temporal x(t) es la diferencia entre el tiempo nominal esperado y el tiempo normal real:
Para los valores medidos se define una serie de errores temporales TE(t) a partir de la función temporal de referencia Tref(t) como
Función de frecuencia
editarLa función de frecuencia es la frecuencia a lo largo del tiempo, definida como
Frecuencia fraccionaria
editarLa frecuencia fraccionaria y(t) es la diferencia normalizada entre la frecuencia y la frecuencia nominal :
Frecuencia fraccionaria media
editarLa frecuencia fraccionaria media se define como
donde la media se toma sobre el tiempo de observación , y(t) es el error de frecuencia fraccional en el tiempo t, y es el tiempo de observación.
Como y(t) es la derivada de x(t), podemos reescribirla sin pérdida de generalidad como
Estimadores
editarEsta definición se basa en el valor estadístico esperado, que se integra en un tiempo infinito. La situación en el mundo real no permite este tipo de series temporales, en cuyo caso es necesario utilizar un estimador estadístico en su lugar. Se presentarán y discutirán varios estimadores diferentes.
Convenciones
editar- El número de muestras de frecuencia en una serie de frecuencia fraccionaria se denota con M.
- El número de muestras de error temporal en una serie de error temporal se denota con N.
La relación entre el número de muestras de frecuencia fraccionaria y la serie de errores temporales se fija en la relación
- Para las series de muestras de errores temporales, xi se refiere a la muestra i de la función de tiempo continuo x(t) dada por
- Para las series muestrales de Frecuencia fraccionaria media, se refiere a la muestra i de la función continua de frecuencia fraccionaria media y(t) dada por
- El tiempo entre las mediciones se denota con T, que es la suma del tiempo de observación τ y el tiempo muerto.
Estimadores de τ fijo
editarUn primer estimador sencillo sería traducir directamente la definición en
o para las series temporales:
Sin embargo, estas fórmulas sólo proporcionan el cálculo para el caso . Para calcular para un valor diferente de , es necesario proporcionar una nueva serie temporal.
Estimadores τ de variables no solapadas
editarSi se toma la serie temporal y se salta más allá de n - 1 muestras, se obtendría una nueva serie temporal (más corta) con como tiempo entre las muestras adyacentes, para la que se podría calcular la varianza de Allan con los estimadores simples. Éstos podrían modificarse para introducir la nueva variable n, de modo que no habría que generar una nueva serie temporal, sino que podría reutilizarse la serie temporal original para diversos valores de n. Los estimadores se convierten en
con
y para la serie temporal:
con
Estos estimadores tienen un inconveniente importante, ya que dejan caer una cantidad significativa de datos de la muestra, ya que sólo se utiliza 1/n de las muestras disponibles.
Estimadores τ de variables superpuestas
editarUna técnica presentada por J. J. Snyder[7] proporcionaba una herramienta mejorada, ya que las mediciones se superponían en n series superpuestas de la serie original. Howe, Allan y Barnes[8] introdujeron el estimador de varianza de Allan superpuesto, que puede demostrarse que es equivalente a promediar las muestras de tiempo o de frecuencia normalizada en bloques de n muestras antes del procesamiento. El predictor resultante es
o, para la serie temporal:
Los estimadores solapados tienen un rendimiento muy superior al de los estimadores no solapados a medida que n aumenta y la serie temporal es de longitud moderada. Los estimadores solapados han sido aceptados como los estimadores de varianza de Allan preferidos en las normas IEEE[4], UIT-T[9] y ETSI[10] para mediciones comparables, como las necesarias para la calificación de las telecomunicaciones.
Varianza de Allan modificada
editarPara solucionar la incapacidad de separar la modulación de fase blanca de la modulación de fase de parpadeo utilizando los estimadores de varianza de Allan tradicionales, un filtrado algorítmico reduce el ancho de banda en n. Este filtrado proporciona una modificación a la definición y a los estimadores y ahora se identifica como una clase de varianza separada llamada varianza Allan modificada. La medida de la varianza de Allan modificada es una medida de estabilidad de la frecuencia, al igual que la varianza de Allan.
Estimadores de estabilidad temporal
editarA partir de la desviación Allan modificada (MDEV) puede calcularse una medida estadística de estabilidad temporal ( ), que suele denominarse desviación temporal (TDEV). La TDEV se basa en la MDEV en lugar de la desviación de Allan original, porque la MDEV puede discriminar entre la modulación de fase (PM) blanca y la de parpadeo. A continuación se presenta la estimación de la varianza temporal basada en la varianza de Allan modificada:
y de forma similar para la desviación modificada de Allan a la desviación temporal:
La TDEV se normaliza de forma que sea igual a la desviación clásica para el PM blanco para la constante de tiempo . Para entender el factor de escala de normalización entre las medidas estadísticas, la siguiente es la regla estadística pertinente: Para variables aleatorias independientes X e Y, la varianza ( ) de una suma o diferencia (z = x - y) es la suma cuadrada de sus varianzas ( ). La varianza de la suma o diferencia (y = x2τ - xτ) de dos muestras independientes de una variable aleatoria es el doble de la varianza de la variable aleatoria ( ). El MDEV es la segunda diferencia de las medidas de fase independientes (x) que tienen una varianza ( ). Como el cálculo es la doble diferencia, que requiere tres mediciones de fase independientes (x2τ - 2xτ + x), la varianza de Allan modificada (MVAR) es tres veces las varianzas de las mediciones de fase.
Otros estimadores
editarOtros desarrollos han producido métodos de estimación mejorados para la misma medida de estabilidad, la varianza/desviación de la frecuencia, pero se conocen con nombres distintos como la varianza de Hadamard, la varianza de Hadamard modificada, la varianza total, la varianza total modificada y la varianza de Theo. Estas se distinguen por un mejor uso de la estadística para mejorar los límites de confianza o la capacidad de manejar la deriva lineal de la frecuencia.
Intervalos de confianza y grados de libertad equivalentes
editarLos estimadores estadísticos calcularán un valor estimado sobre la serie de muestras utilizada. Las estimaciones pueden desviarse del valor real y el rango de valores que, con cierta probabilidad, contendrá el valor real se denomina intervalo de confianza. El intervalo de confianza depende del número de observaciones de la serie muestral, del tipo de ruido dominante y del estimador utilizado. La anchura también depende de la certeza estadística para la que los valores del intervalo de confianza forman un rango acotado, por lo que la certeza estadística de que el valor verdadero está dentro de ese rango de valores. En el caso de los estimadores variables-τ, el múltiplo n de τ0 también es una variable.
Intervalo de confianza
editarEl intervalo de confianza puede establecerse mediante la distribución chi-cuadrado utilizando la distribución de la varianza de la muestra:[4][8]
donde s2 es la varianza muestral de nuestra estimación, σ2 es el valor de la varianza verdadera, df son los grados de libertad para el estimador, y χ2 son los grados de libertad para una determinada probabilidad. Para una probabilidad del 90 %, que cubre el rango del 5 % al 95 % en la curva de probabilidad, los límites superior e inferior se pueden encontrar utilizando la desigualdad
que después de reordenar para la varianza verdadera se convierte en
Grados de libertad efectivos
editarLos grados de libertad representan el número de variables libres capaces de contribuir a la estimación. Dependiendo del estimador y del tipo de ruido, los grados de libertad efectivos varían. Se han encontrado empíricamente fórmulas de estimadores que dependen de N y n:[8]
| Tipo de ruido | Grados de libertad |
|---|---|
| modulación de fase blanca (WPM) | |
| modulación de fase de parpadeo (FPM) | |
| modulación de frecuencia blanca (WFM) | |
| modulación de frecuencia de parpadeo (FFM) | |
| modulación de frecuencia aleatoria (RWFM) |
Ruido de potencia
editarLa varianza de Allan tratará los distintos tipos de ruido de ley de potencia de forma diferente, lo que permite identificarlas y estimar su intensidad. Como convención, la anchura del sistema de medición (frecuencia de esquina alta) se denota fH.
| Tipo de ruido de potencia | Pendiente de ruido de fase | Pendiente de ruido en frecuencia | Coeficiente de potencia | Ruido de fase |
Varianza de Allan |
Desviación de Allan |
|---|---|---|---|---|---|---|
| modulación de fase blanca (WPM) | ||||||
| modulación de fase de parpadeo (FPM) | ||||||
| modulación de frecuencia blanca (WFM) | ||||||
| modulación de frecuencia de parpadeo (FFM) | ||||||
| modulación de frecuencia aleatoria (RWFM) |
Tal y como se encuentra en[11][12] y en formas modernas[13][14].
La varianza de Allan es incapaz de distinguir entre WPM y FPM, pero es capaz de resolver los otros tipos de ruido de ley de potencia. Para distinguir WPM y FPM, es necesario emplear la varianza de Allan modificada.
Las fórmulas anteriores suponen que
y, por tanto, que el ancho de banda del tiempo de observación sea mucho menor que el ancho de banda de los instrumentos. Cuando no se cumple esta condición, todas las formas de ruido dependen del ancho de banda del instrumento.
Mapeo α-μ
editarEl mapeo detallado de una modulación de fase de la forma
donde
o una modulación de frecuencia de la forma
en la varianza de Allan de la forma
puede simplificarse significativamente proporcionando un mapeo entre α y μ. También se presenta un mapeo entre α y Kα por conveniencia:[4]
| α | β | μ | Kα |
|---|---|---|---|
| −2 | −4 | 1 | |
| −1 | −3 | 0 | |
| 0 | −2 | −1 | |
| 1 | −1 | −2 | |
| 2 | 0 | −2 |
Conversión general del ruido de fase
editarUna señal con ruido espectral de fase con unidades rad2/Hz puede ser convertida a Varianza Allan por:[14]
Respuesta lineal
editarAunque la varianza de Allan está pensada para distinguir las formas de ruido, dependerá de algunas respuestas lineales al tiempo, pero no de todas. Se indican en la tabla:
Respuesta lineal de la varianza de Allan Efecto lineal respuesta temporal respuesta de frecuencia Varianza de Allan Desviación de Allan desplazamiento de fase desplazamiento de frecuencia deriva lineal
Por lo tanto, la deriva lineal contribuirá al resultado de la salida. Cuando se mide un sistema real puede ser necesario estimar la deriva lineal u otro mecanismo de deriva y eliminarla de la serie temporal antes de calcular la varianza de Allan.[13]
Propiedades de los filtros de tiempo y frecuencia
editarAl analizar las propiedades de la varianza de Allan y sus amigas, ha resultado útil considerar las propiedades del filtro en la frecuencia normalizada. Partiendo de la definición de la varianza de Allan para
dónde
Sustituyendo la serie temporal de por la variante transformada de Fourier la varianza de Allan puede expresarse en el dominio de la frecuencia como
Así, la función de transferencia de la varianza de Allan es
Funciones de sesgo
editarLa varianza de la muestra M y el caso especial definido de la varianza de Allan experimentará un sesgo sistemático dependiendo del diferente número de muestras M y de la diferente relación entre T y τ. Para tratar estos sesgos se han definido las funciones de sesgo B1 y B2[15] y permiten la conversión entre diferentes valores de M y T.
Estas funciones de sesgo no son suficientes para tratar el sesgo resultante de concatenar M muestras al tiempo de observación Mτ0 sobre el MT0 con el tiempo muerto distribuido entre los M bloques de medición en lugar de al final de la medición. Esto hizo que se necesitara el sesgo B3.[16]
Las funciones de sesgo se evalúan para un valor particular de µ, por lo que el mapeo α-µ debe realizarse para la forma de ruido dominante, tal y como se ha encontrado mediante la identificación del ruido. Alternativamente,[3][15] el valor de µ de la forma de ruido dominante puede inferirse a partir de las mediciones utilizando las funciones de sesgo.
Función de sesgo B1
editarLa función de sesgo B1 relaciona la varianza de la muestra M con la varianza de la muestra 2 (varianza de Allan), manteniendo constantes el tiempo entre mediciones T y el tiempo de cada medición τ. Se define[15] como
donde
La función de sesgo se convierte tras el análisis en
Función de sesgo B2
editarLa función de sesgo B2 relaciona la varianza de 2 muestras para el tiempo de muestreo T con la varianza de 2 muestras (varianza de Allan), manteniendo el número de muestras N = 2 y el tiempo de observación τ constantes. Se define[15] como
donde
La función de sesgo se convierte tras el análisis en
Función de sesgo B3
editarLa función de sesgo B3 relaciona la varianza de dos muestras para el tiempo de muestreo MT0 y el tiempo de observación Mτ0 con la varianza de dos muestras (varianza de Allan) y se define[16] como
donde
La función de sesgo B3 es útil para ajustar los valores del estimador de la variable τ no solapada y solapada basada en las mediciones del tiempo muerto de la observación τ0 y el tiempo entre las observaciones T0 a las estimaciones normales del tiempo muerto.
La función de sesgo se convierte después del análisis (para el caso N = 2) en
donde
Función de sesgo τ
editarAunque no se ha formulado formalmente, se ha deducido indirectamente como consecuencia del mapeo α-µ. Cuando se comparan dos medidas de varianza de Allan para diferentes τ, suponiendo el mismo ruido dominante en la forma del mismo coeficiente µ, se puede definir un sesgo como
La función de sesgo se convierte tras el análisis en
Conversión entre valores
editarPara convertir de un conjunto de medidas a otro se pueden ensamblar las funciones de sesgo B1, B2 y τ. En primer lugar, la función B1 convierte el valor (N1, T1, τ1) en (2, T1, τ1), a partir del cual la función B2 lo convierte en un valor (2, τ1, τ1), es decir, la varianza de Allan en τ1. La medida de la varianza de Allan se puede convertir mediante la función de sesgo τ de τ1 a τ2, de la que se obtiene el valor (2, T2, τ2) mediante B2 y finalmente mediante B1 en la varianza (N2, T2, τ2). La conversión completa se convierte en:
donde
Del mismo modo, para las mediciones concatenadas utilizando M secciones, la extensión lógica se convierte en
Problemas de medición
editarCuando se realizan mediciones para calcular la varianza Allan o la desviación Allan hay una serie de cuestiones que pueden hacer que las mediciones degeneren. Aquí se tratan los efectos específicos de la varianza Allan, donde los resultados estarían sesgados.
Límites del ancho de banda de las mediciones
editarSe espera que un sistema de medición tenga un ancho de banda igual o inferior al de la tasa de Nyquist, como se describe en el teorema de Shannon-Hartley. Como puede verse en las fórmulas de ruido de potencia, las modulaciones de ruido blanco y de parpadeo dependen ambas de la frecuencia de esquina superior (se supone que estos sistemas están filtrados solamente en paso bajo). Teniendo en cuenta la propiedad del filtro de frecuencia se puede ver claramente que el ruido de baja frecuencia tiene un mayor impacto en el resultado. Para los tipos de ruido de modulación de fase relativamente planos (por ejemplo, WPM y FPM), el filtrado tiene relevancia, mientras que para los tipos de ruido con mayor pendiente el límite superior de la frecuencia adquiere menos importancia, suponiendo que el ancho de banda del sistema de medición es amplio en relación con el τ como viene dado por
Cuando no se cumple este supuesto, el ancho de banda efectivo debe anotarse junto a la medición. Los interesados deben consultar la norma NBS TN394.
Sin embargo, si se ajusta el ancho de banda del estimador utilizando múltiplos enteros del tiempo de muestreo , entonces el impacto del ancho de banda del sistema puede reducirse a niveles insignificantes. En el caso de las necesidades de las telecomunicaciones, estos métodos han sido necesarios para garantizar la comparabilidad de las mediciones y permitir cierta libertad a los proveedores para realizar diferentes implementaciones. La Rec. G.813[17] para la medición del TDEV.
Se puede recomendar que los primeros múltiplos de τ0 sean ignorados, de manera que la mayor parte del ruido detectado se encuentre dentro de la banda de paso del ancho de banda de los sistemas de medición.
Se realizaron desarrollos adicionales en la varianza de Allan para permitir que el ancho de banda del hardware se redujera por medio de software. Este desarrollo de un ancho de banda por software permitió abordar el ruido restante, y el método se denomina ahora varianza de Allan modificada. Esta técnica de reducción del ancho de banda no debe confundirse con la variante mejorada de la varianza de Allan modificada, que también modifica el ancho de banda de un filtro de suavizado.
Tiempo muerto en las mediciones
editarMuchos instrumentos de medición de tiempo y frecuencia tienen las etapas de tiempo de armado, tiempo de base, tiempo de procesamiento y pueden volver a disparar el armado. El tiempo de armado va desde el momento en que se activa el armado hasta que se produce el evento de inicio en el canal de inicio. El tiempo base asegura que transcurra una cantidad mínima de tiempo antes de aceptar un evento en el canal de parada como evento de parada. El número de eventos y el tiempo transcurrido entre el evento de inicio y el de parada se registra y se presenta durante el tiempo de procesamiento. Cuando se produce el procesamiento (también conocido como tiempo de permanencia), el instrumento normalmente no puede realizar otra medición. Tras el procesamiento, un instrumento en modo continuo vuelve a activar el circuito de armado. El tiempo entre el evento de parada y el siguiente evento de arranque se convierte en tiempo muerto, durante el cual no se observa la señal. Este tiempo muerto introduce sesgos de medición sistemáticos, que deben ser compensados para obtener resultados adecuados. En este tipo de sistemas de medición, el tiempo T indica el tiempo entre los eventos de arranque adyacentes (y, por tanto, las mediciones), mientras que τ denota la longitud de la base de tiempo, es decir, la longitud nominal entre el evento de inicio y el de parada de cualquier medición.
Los efectos del tiempo muerto en las mediciones tienen tal impacto en el resultado producido que se ha estudiado mucho este campo para cuantificar adecuadamente sus propiedades. La introducción de los contadores de tiempo muerto cero eliminó la necesidad de este análisis. Un contador de tiempo muerto cero tiene la propiedad de que el evento de parada de una medición se utiliza también como evento de inicio del siguiente evento. Estos contadores crean una serie de pares de marcas de tiempo de eventos y tiempo, uno para cada canal espaciado por la base de tiempo. Estas mediciones también han demostrado ser útiles en las formas de orden de análisis de series temporales.
Las mediciones que se realizan con tiempo muerto pueden corregirse mediante la función de sesgo B1, B2 y B3. Así pues, el tiempo muerto como tal no prohíbe el acceso a la varianza de Allan, pero lo hace más problemático. El tiempo muerto debe ser conocido, de manera que se pueda establecer el tiempo entre muestras T.
Longitud de la medición y uso efectivo de las muestras
editarEstudiando el efecto que tiene sobre los intervalos de confianza la longitud N de la serie de muestras, y el efecto de la variable τ parámetro n los intervalos de confianza pueden llegar a ser muy grandes, ya que los grados de libertad efectivos pueden llegar a ser pequeños para alguna combinación de N y n para la forma de ruido dominante (para eseτ).
El efecto puede ser que el valor estimado sea mucho menor o mucho mayor que el valor real, lo que puede llevar a conclusiones falsas del resultado.
Se recomienda que el intervalo de confianza se represente junto con los datos, de forma que el lector del gráfico pueda ser consciente de la incertidumbre estadística de los valores.
Se recomienda que la longitud de la secuencia de muestras, es decir, el número de muestras N, se mantenga alta para garantizar que el intervalo de confianza sea pequeño en el rango τ de interés.
Se recomienda que el rango de τ barrido por el multiplicador n de τ0 esté limitado en el extremo superior relativo a N, de forma que la lectura del gráfico no se vea confundida por valores de estimadores muy inestables.
Se recomienda que los estimadores que proporcionan mejores valores de grados de libertad se utilicen en sustitución de los estimadores de la varianza de Allan o como complemento de éstos cuando superen a los estimadores de la varianza de Allan. Entre ellos deben considerarse los estimadores de la varianza total y de la varianza de Theo.
Tipo de ruido dominante
editarUn gran número de constantes de conversión, correcciones de sesgo e intervalos de confianza dependen del tipo de ruido dominante. Para una interpretación adecuada, el tipo de ruido dominante para el τ particular de interés debe ser identificado a través de la identificación del ruido. Si no se identifica el tipo de ruido dominante, se obtendrán valores sesgados. Algunos de estos sesgos pueden ser de varios órdenes de magnitud, por lo que pueden ser de gran importancia.
Deriva lineal
editarLos efectos sistemáticos sobre la señal se cancelan sólo parcialmente. El desplazamiento de fase y de frecuencia se cancela, pero la deriva lineal u otras formas de alto grado de las curvas de fase polinómicas no se cancelarán y, por lo tanto, constituirán una limitación de la medición. Se puede emplear el ajuste de la curva y la eliminación del desplazamiento sistemático. A menudo, la eliminación de la deriva lineal puede ser suficiente. También se pueden utilizar estimadores de deriva lineal como la varianza de Hadamard. Se podría emplear la eliminación de la deriva lineal mediante un estimador basado en el momento.
Sesgo del estimador del instrumento de medición
editarLos instrumentos tradicionales sólo permitían medir eventos individuales o pares de eventos. La introducción de la herramienta estadística mejorada de las mediciones superpuestas por J. J. Snyder permitió una resolución mucho mejor en las lecturas de frecuencia, rompiendo el equilibrio tradicional de dígitos/base de tiempo. Aunque estos métodos son útiles para su propósito, el uso de estas mediciones suavizadas para el cálculo de la varianza de Allan daría una falsa impresión de alta resolución,[18][19] pero para una τ más larga el efecto desaparece gradualmente, y la región inferior a la τ de la medición tiene valores sesgados. Este sesgo proporciona valores más bajos de lo que debería, por lo que es un sesgo demasiado optimista (suponiendo que los números bajos sean lo que se desea), que reduce la utilidad de la medición en lugar de mejorarla. Estos algoritmos inteligentes suelen poder desactivarse o sortearse utilizando el modo de sello de tiempo, que es muy preferible si está disponible.
Mediciones prácticas
editarAunque se pueden idear varios enfoques para la medición de la varianza de Allan, un ejemplo sencillo puede ilustrar cómo se pueden realizar las mediciones.
Medición
editarTodas las mediciones de la varianza de Allan serán, en efecto, la comparación de dos relojes diferentes. Consideremos un reloj de referencia y un dispositivo bajo prueba (DUT), y ambos con una frecuencia nominal común de 10 MHz. Se utiliza un contador de intervalos de tiempo para medir el tiempo entre el flanco de subida de la referencia (canal A) y el flanco de subida del dispositivo bajo prueba.
Para proporcionar mediciones uniformemente espaciadas, el reloj de referencia se dividirá para formar la tasa de medición, disparando el contador de intervalo de tiempo (entrada ARM). Esta tasa puede ser de 1 Hz (utilizando la salida de 1 PPS de un reloj de referencia), pero también se pueden utilizar otras tasas como 10 Hz y 100 Hz. La velocidad con la que el contador de intervalos de tiempo puede completar la medición, emitir el resultado y prepararse para el siguiente brazo limitará la frecuencia de disparo.
A continuación, un ordenador es útil para registrar la serie de diferencias de tiempo observadas.
Posprocesamiento
editarLas series de tiempo registradas requieren un post-procesamiento para desenvolver la fase envuelta, de tal manera que se está proporcionando un error de fase continuo. Si es necesario, también deben corregirse los errores de registro y medición. Se debe realizar una estimación y eliminación de la deriva, y se debe identificar y comprender el mecanismo de deriva de las fuentes. Las limitaciones de la deriva en las mediciones pueden ser severas, por lo que es necesario dejar que los osciladores se estabilicen, mediante un tiempo suficiente de encendido.
La varianza de Allan puede entonces calcularse utilizando los estimadores dados, y para fines prácticos el estimador de solapamiento debe ser utilizado debido a su uso superior de los datos sobre el estimador de no solapamiento. También podrían utilizarse otros estimadores, como los de varianza total o Theo, si se aplican correcciones de sesgo que proporcionen resultados compatibles con la varianza de Allan.
Para formar los gráficos clásicos, la desviación de Allan (raíz cuadrada de la varianza de Allan) se traza en formato log-log contra el intervalo de observación τ.
Equipo y software
editarEl contador de intervalos de tiempo suele ser un contador disponible en el mercado. Los factores limitantes son la resolución de un solo disparo, la fluctuación del disparo, la velocidad de las mediciones y la estabilidad del reloj de referencia. La recopilación y el posprocesamiento informáticos pueden realizarse mediante programas informáticos comerciales o de dominio público ya existentes. Existen soluciones muy avanzadas que permiten medir y calcular en una sola caja.
Historia de la investigación
editarEl campo de la estabilidad en frecuencia se ha estudiado durante mucho tiempo. Sin embargo, durante la década de 1960 se constató que faltaban definiciones coherentes. Un Simposio NASA-IEEE sobre la estabilidad a corto plazo celebrado en noviembre de 1964[20] dio lugar al número especial de febrero de 1966 de las Actas del IEEE sobre la estabilidad de la frecuencia.
El Simposio NASA-IEEE reunió muchos campos y usos de la estabilidad a corto y largo plazo, con artículos de muchos colaboradores diferentes. Los artículos y las discusiones del panel coinciden en la existencia del ruido de parpadeo de la frecuencia y en el deseo de lograr una definición común para la estabilidad a corto y largo plazo.
En las Actas del IEEE sobre la estabilidad de la frecuencia aparecieron importantes artículos, como los de David Allan,[3] James A. Barnes,[21] L. S. Cutler y C. L. Searle[1] y D. B. Leeson,[2] que contribuyeron a dar forma al campo.
El artículo de David Allan analiza la varianza clásica de la frecuencia de la muestra M, abordando la cuestión del tiempo muerto entre las mediciones junto con una función de sesgo inicial[3] Aunque la función de sesgo inicial de Allan supone que no hay tiempo muerto, sus fórmulas incluyen cálculos de tiempo muerto. Su artículo analiza el caso de M muestras de frecuencia (llamadas N en el artículo) y estimadores de varianza. Proporciona la cartografía α-µ, ahora estándar, basándose claramente en el trabajo de James Barnes[21] en el mismo número.
El caso de la varianza de 2 muestras es un caso especial de la varianza de M muestras, que produce un promedio de la derivada de la frecuencia. Allan utiliza implícitamente la varianza de 2 muestras como caso base, ya que para una M elegida arbitrariamente, los valores pueden transferirse a través de la varianza de 2 muestras a la varianza de M. No se ha manifestado claramente ninguna preferencia por la varianza de 2 muestras, aunque se hayan facilitado las herramientas. Sin embargo, este artículo sentó las bases para utilizar la varianza de 2 muestras como forma de comparar otras varianzas de muestras M.
James Barnes amplió significativamente el trabajo sobre las funciones de sesgo,[15] introduciendo las modernas funciones de sesgo B1 y B2. Curiosamente, se refiere a la varianza de la muestra M como "varianza de Allan", haciendo referencia al artículo de Allan "Statistics of Atomic Frequency Standards"[3] Con estas funciones de sesgo modernas, se podía realizar una conversión completa entre las medidas de varianza de la muestra M de varios valores M, T y τ, mediante la conversión a través de la varianza de 2 muestras.
James Barnes y David Allan ampliaron las funciones de sesgo con la función B3[16] para manejar el sesgo del estimador de muestras concatenadas. Esto era necesario para manejar el nuevo uso de observaciones de muestras concatenadas con tiempo muerto entre ellas.
En 1970, el Comité Técnico de Frecuencia y Tiempo del IEEE, dentro del Grupo de Instrumentación y Mediciones del IEEE, proporcionó un resumen del campo, publicado como NBS Technical Notice 394.[11] Este documento fue el primero de una serie de documentos más educativos y prácticos que ayudaban a los ingenieros a comprender el campo. Este documento recomendaba la varianza de 2 muestras con T = τ, refiriéndose a ella como varianza de Allan (ahora sin las comillas). La elección de esta parametrización permite manejar bien algunas formas de ruido y obtener mediciones comparables; es esencialmente el mínimo común denominador con la ayuda de las funciones de sesgo B1 y B2.
J. J. Snyder propuso un método mejorado para la estimación de la frecuencia o la varianza, utilizando estadísticas muestrales para los contadores de frecuencia.[7] Para obtener más grados de libertad efectivos del conjunto de datos disponible, el truco consiste en utilizar períodos de observación superpuestos. Esto proporciona una mejora de , y se incorporó en el estimador de varianza de Allan solapado.[8] Este desarrollo mejoró los estimadores de varianza de Allan clásicos, proporcionando asimismo una inspiración directa para el trabajo sobre la varianza de Allan modificada.
Howe, Allan y Barnes presentaron el análisis de los intervalos de confianza, los grados de libertad y los estimadores establecidos.[8]
Recursos educativos y prácticos
editarEl campo del tiempo y la frecuencia y el uso de la varianza de Allan, la desviación de Allan y sus amigos es un campo que implica muchos aspectos, para los que tanto la comprensión de los conceptos como las mediciones prácticas y el posprocesamiento requieren cuidado y comprensión. Por ello, se dispone de un conjunto de material didáctico que abarca unos 40 años. Dado que éstos reflejan la evolución de la investigación de su época, se centran en la enseñanza de diferentes aspectos a lo largo del tiempo, en cuyo caso un estudio de los recursos disponibles puede ser una forma correcta de encontrar el recurso adecuado.
El primer resumen significativo es la Nota Técnica 394 de la NBS "Caracterización de la estabilidad de la frecuencia"[11], producto del Comité Técnico de Frecuencia y Tiempo del Grupo de Instrumentación y Medición del IEEE. Ofrece la primera visión general del campo, enunciando los problemas, definiendo las definiciones básicas de apoyo y entrando en la varianza de Allan, las funciones de sesgo B1 y B2, la conversión de las medidas en el dominio del tiempo. Es útil, ya que es una de las primeras referencias que tabulan la varianza de Allan para los cinco tipos básicos de ruido.
Una referencia clásica es la Monografía 140 de la NBS[22] de 1974, que en su capítulo 8 detalla las "Estadísticas del análisis de datos de tiempo y frecuencia".[23] Es la variante ampliada de la Nota Técnica 394 de la NBS y añade esencialmente en las técnicas de medición y el tratamiento práctico de los valores.
Cubre el uso efectivo de los datos, los intervalos de confianza, el grado de libertad efectivo, introduciendo asimismo el estimador de varianza de Allan superpuesto. Es una lectura muy recomendable para estos temas.
La norma IEEE 1139 Standard definitions of Physical Quantities for Fundamental Frequency and Time Metrology[4] es, más que una norma, una referencia completa y un recurso educativo.
Un libro moderno orientado a la telecomunicación es el de Stefano Bregni "Synchronisation of Digital Telecommunication Networks"[13], que resume no sólo el campo, sino también gran parte de su investigación en la materia hasta ese momento. Pretende incluir tanto las medidas clásicas como las específicas de las telecomunicaciones, como la MTIE. Es un compañero práctico cuando se examinan las medidas relacionadas con las normas de telecomunicaciones.
La publicación especial 1065 del NIST "Handbook of Frequency Stability Analysis" de W. J. Riley[13] es una lectura recomendada para quien quiera dedicarse a este campo. Es rico en referencias y también cubre una amplia gama de medidas, sesgos y funciones relacionadas que un analista moderno debe tener disponible. Además, describe el procesamiento general necesario para una herramienta moderna.
Usos
editarLa varianza Allan se utiliza como medida de la estabilidad de la frecuencia en una variedad de osciladores de precisión, como los osciladores de cristal, los relojes atómicos y los láseres estabilizados en frecuencia durante un período de un segundo o más. La estabilidad a corto plazo (menos de un segundo) suele expresarse como ruido de fase. La varianza de Allan también se utiliza para caracterizar la estabilidad de sesgo de los giroscopios, incluidos los giroscopios de fibra óptica, los giroscopios de resonador hemisférico y los giroscopios y acelerómetros MEMS.[24][25]
50.º Aniversario
editarEn 2016, el IEEE-UFFC publicó un "Número especial para celebrar el 50º aniversario de la Varianza Allan (1966-2016)". El editor invitado para ese número fue el antiguo colega de David en el NIST, Judah Levine, que en 2016 era el último galardonado con el premio I. I. Rabi.
Véase también
editarReferencias
editar- ↑ a b Cutler, L. S.; Searle, C. L. (febrero de 1966), «Some Aspects of the Theory and Measurements of Frequency Fluctuations in Frequency Standards», Proceedings of the IEEE (en inglés) 54 (2): 136-154, doi:10.1109/proc.1966.4627.
- ↑ a b c Leeson, D. B (febrero de 1966), «A simple Model of Feedback Oscillator Noise Spectrum», Proceedings of the IEEE (en inglés) 54 (2): 329-330, doi:10.1109/proc.1966.4682, archivado desde el original el 1 de febrero de 2014, consultado el 20 de septiembre de 2012.
- ↑ a b c d e f Allan, D. Statistics of Atomic Frequency Standards, pages 221–230. Proceedings of the IEEE, Vol. 54, No 2, febrero de 1966.
- ↑ a b c d e «Definitions of physical quantities for fundamental frequency and time metrology – Random Instabilities». IEEE STD 1139-1999 (en inglés). 1999. ISBN 978-0-7381-1753-9. doi:10.1109/IEEESTD.1999.90575.
- ↑ Rubiola, Enrico (2008), Phase Noise and Frequency Stability in Oscillators, Cambridge university press, ISBN 978-0-521-88677-2.
- ↑ http://www.allanstime.com/Publications/DWA/Conversion_from_Allan_variance_to_Spectral_Densities.pdf. Archivado el 6 de febrero de 2012 en Wayback Machine.
- ↑ a b Snyder, J.J. (1981). «An Ultra-High Resolution Frequency Meter». Thirty Fifth Annual Frequency Control Symposium (IEEE). doi:10.1109/freq.1981.200513. Consultado el 25 de febrero de 2022.
- ↑ a b c d e Howe, D.A.; Allan, D.U.; Barnes, J.A. (1981). «Properties of Signal Sources and Measurement Methods». Thirty Fifth Annual Frequency Control Symposium (IEEE). doi:10.1109/freq.1981.200541. Consultado el 25 de febrero de 2022.
- ↑ DIN EN 61883-7:2003-08, Audio/Video-Geräte der Unterhaltungselektronik_- Digitale Schnittstelle_- Teil_7: Übertragung nach Rec. ITU-R_BO.1294 System_B (IEC_61883-7:2003); Deutsche Fassung EN_61883-7:2003, Beuth Verlag GmbH, consultado el 25 de febrero de 2022.
- ↑ ETSI ITS-G5 Standard. Springer International Publishing. 2020. pp. 442-442. Consultado el 25 de febrero de 2022.
- ↑ a b c Barnes, James A.; Chi, Andrew R.; Cutler, Leonard S.; Healey, Daniel J.; Leeson, David B.; McGunigal, Thomas E.; Mullen, James A.; Smith, Warren L. et al. (1971-05). «Characterization of Frequency Stability». IEEE Transactions on Instrumentation and Measurement. IM-20 (2): 105-120. ISSN 0018-9456. doi:10.1109/tim.1971.5570702. Consultado el 26 de febrero de 2022.
- ↑ Barnes, James A.; Chi, Andrew R.; Cutler, Leonard S.; Healey, Daniel J.; Leeson, David B.; McGunigal, Thomas E.; Mullen, James A.; Smith, Warren L. et al. (1971-05). «Characterization of Frequency Stability». IEEE Transactions on Instrumentation and Measurement. IM-20 (2): 105-120. ISSN 0018-9456. doi:10.1109/tim.1971.5570702. Consultado el 26 de febrero de 2022.
- ↑ a b c d Bregni, Stefano (2002). Synchronization of digital telecommunications networks. Wiley. ISBN 0-470-85215-1. OCLC 51723879. Consultado el 26 de febrero de 2022.
- ↑ a b Toth, Patricia (2017-11). NIST MEP cybersecurity self-assessment handbook for assessing NIST SP 800-171 security requirements in response to DFARS cybersecurity requirements. National Institute of Standards and Technology. Consultado el 26 de febrero de 2022.
- ↑ a b c d e Barnes, J A (1969). Tables of bias functions, B₁ and B₂, for variances based on finite samples of processes with power law spectral densities. National Bureau of Standards. Consultado el 26 de febrero de 2022.
- ↑ a b c Barnes, J A (1990). Variances based on data with dead time between the measurements. National Bureau of Standards. Consultado el 26 de febrero de 2022.
- ↑ ITU-T Rec. G.813: Timing characteristics of SDH equipment slave clock (SEC), ITU-T Rec. G.813 (03/2003).
- ↑ Rubiola, E.; Vernotte, F.; Giordano, V. «On the measurement of frequency and of its sample variance with high-resolution counters». Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, 2005. (IEEE). doi:10.1109/freq.2005.1573901. Consultado el 27 de febrero de 2022.
- ↑ JPL, CALTECH, AND NASA:. Yale University Press. pp. 134-160. Consultado el 27 de febrero de 2022.
- ↑ Razenkova, Elena; Radeloff, Volker C.; Dubinin, Maxim; Bragina, Eugenia V.; Allen, Andrew M.; Clayton, Murray K.; Pidgeon, Anna M.; Baskin, Leonid M. et al. (21 de enero de 2020). «Vegetation productivity summarized by the Dynamic Habitat Indices explains broad-scale patterns of moose abundance across Russia». Scientific Reports 10 (1). ISSN 2045-2322. doi:10.1038/s41598-019-57308-8. Consultado el 27 de febrero de 2022.
- ↑ a b Barnes, J.A. (1966). «Atomic timekeeping and the statistics of precision signal generators». Proceedings of the IEEE 54 (2): 207-220. ISSN 0018-9219. doi:10.1109/proc.1966.4633. Consultado el 27 de febrero de 2022.
- ↑ Blair, Byron E (1974). Time and frequency :. National Bureau of Standards. Consultado el 27 de febrero de 2022.
- ↑ Brandenberger, H.; Hadorn, F.; Halford, D.; Shoaf, J.H. (1971). «High Quality Quartz Crystal Oscillators: Frequency Domain and Time Domain Stability». 25th Annual Symposium on Frequency Control (IEEE). doi:10.1109/freq.1971.199861. Consultado el 27 de febrero de 2022.
- ↑ «Mechanica».
- ↑ Bose, S.; Gupta, A. K.; Handel, P. (September 2017). "On the noise and power performance of a shoe-mounted multi-IMU inertial positioning system". 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN): 1–8. doi:10.1109/IPIN.2017.8115944. ISBN 978-1-5090-6299-7. S2CID 19055090.
Enlaces externos
editar- Recursos didácticos para el control de la frecuencia de la UFFC
- Herramienta de búsqueda de publicaciones del NIST
- Visión general de la varianza de David W. Allan
- Sitio web oficial de David W. Allan
- Publicaciones del JPL - Análisis de ruido y estadísticas
- Publicaciones de William Riley
- Stable32 Archivado el 23 de junio de 2018 en Wayback Machine., Software para el análisis de la estabilidad de la frecuencia, por William Riley
- Publicaciones de Stefano Bregni
- Publicaciones de Enrico Rubiola
- Allanvar: Paquete de R para la caracterización de errores de sensores mediante la varianza de Allan
- Software Alavar para Windows con herramientas de generación de informes; Freeware
- AllanTools: biblioteca de código abierto en python para la varianza de Allan
- MATLAB AVAR aplicación MATLAB de código abierto




