Cono convexo
En álgebra lineal, un cono, a veces llamado cono lineal para distinguirlo de otros tipos de conos, es un subconjunto de un espacio vectorial que es cerrado bajo la multiplicación escalar positiva; es decir, C es un cono si implica que para cada escalar positivo s.
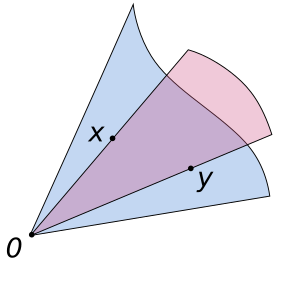
Cuando los escalares son números reales, o pertenecen a un cuerpo ordenado, generalmente se llama cono a un subconjunto de un espacio vectorial que se cierra mediante la multiplicación por un escalar positivo. En este contexto, un cono convexo es un cono que se cierra bajo suma o, de manera equivalente, un subconjunto de un espacio vectorial que se cierra bajo combinación lineal con coeficientes positivos. De ello se deduce que los conos convexos son conjuntos convexos.
En este artículo solo se considera el caso de escalares en un campo ordenado.
Definición
editarUn subconjunto C de un espacio vectorial V sobre un cuerpo ordenado F es un cono (o a veces llamado cono lineal) si para cada x en C y para todo escalar positivo α en F, el producto αx está en C.[1] Téngase en cuenta que algunos autores definen cono con el escalar α que abarca todos los escalares no negativos (en lugar de todos los escalares positivos, que no incluyen el 0).[2]
Un cono C es un cono convexo si αx + βy pertenece a C, para cualquier escalar positivo α, β y cualquier x , y en C.[3][4] Un cono C es convexo si y solo si C + C ⊆ C.
Este concepto es significativo para cualquier espacio vectorial que permita el concepto de escalar "positivo", como espacios sobre los números racionales, los algebraicos o (más comúnmente), los números reales. Debe tenerse en cuenta también que los escalares de la definición son positivos, lo que significa que el origen no tiene por qué pertenecer a C. Algunos autores utilizan una definición que garantiza que el origen pertenece a C.[5] Debido a los parámetros de escala α y β, los conos tienen una extensión infinita y no están acotados.
Si C es un cono convexo, entonces para cualquier escalar positivo α y cualquier x en C, el vector Se deduce que un cono convexo C es un caso especial de un cono lineal.
De la propiedad anterior se deduce que un cono convexo también se puede definir como un cono lineal cerrado bajo combinaciones convexas, o justo bajo la adición. De manera más sucinta, un conjunto C es un cono convexo si y solo si αC= C y C + C= C, para cualquier escalar positivo α.
Ejemplos
editar- Para un espacio vectorial V, el conjunto vacío, el espacio V y cualquier subespacio vectorial de V son conos convexos.
- La combinación cónica de un conjunto finito o infinito de vectores en es un cono convexo.
- Los conos tangentes de un conjunto convexo son conos convexos.
- El conjunto
es un cono pero no un cono convexo.
- El cono norma
es un cono convexo.
- La intersección de dos conos convexos en el mismo espacio vectorial es nuevamente un cono convexo, pero su unión puede no serlo.
- La clase de conos convexos también está cerrada bajo aplicaciones lineales arbitrarias. En particular, si C es un cono convexo, también lo es su opuesto y es el subespacio lineal más grande contenido en C.
- El conjunto de matrices semidefinidas positivas.
- El conjunto de funciones continuas no negativas es un cono convexo.
Ejemplos especiales
editarConos convexos afines
editarUn cono convexo afín es el conjunto resultante de aplicar una transformación afín a un cono convexo.[6] Un ejemplo común es trasladar un cono convexo por un punto p: p + C. Técnicamente, tales transformaciones pueden producir no conos. Por ejemplo, a menos que p = 0, p + C no sea un cono lineal. Sin embargo, todavía se le llama cono convexo afín.
Semiespacios
editarUn hiperplano (lineal) es un conjunto de la forma donde f es un funcional lineal en el espacio vectorial V. Un semiespacio cerrado es un conjunto de la forma o de manera que un semiespacio abierto utiliza una desigualdad estricta.[7][8]
Los semiespacios (abiertos o cerrados) son conos convexos afines. Además (en dimensiones finitas), cualquier cono convexo C que no sea todo el espacio V debe estar contenido en algún semiespacio cerrado H de V. Este es un caso especial del lema de Farkas.
Conos poliédricos y finitamente generados
editarLos conos poliédricos son tipos especiales de conos que se pueden definir de varias maneras:[9]: 256–257
- Un cono C es poliédrico si es la combinación cónica de un número finito de vectores (esta propiedad también se llama generación de manera finita).[10][11] Es decir, hay un conjunto de vectores para que .
- Un cono es poliédrico si es la intersección de un número finito de semiespacios que tienen el 0 en su límite (esto lo demostró Weyl en 1935).
- Un cono C es poliédrico si existe alguna matriz tal que .
- Un cono es poliédrico si es el conjunto solución de un sistema de desigualdades lineales homogéneas. Algebraicamente, cada desigualdad está definida por una fila de la matriz A. Geométricamente, cada desigualdad define un semiespacio que pasa por el origen.
Todo cono finitamente generado es un cono poliédrico, y todo cono poliédrico es un cono finitamente generado.[10] Cada cono poliédrico tiene una representación única como una envolvente cónica de sus generadores extremos, y una representación única de intersecciones de semiespacios, dada cada forma lineal asociada con los semiespacios, que también definen un hiperplano de soporte de cada faceta.[12]
Los conos poliédricos juegan un papel central en la teoría de representación de poliedros. Por ejemplo, el teorema de descomposición de los poliedros establece que cada poliedro se puede escribir como una suma de Minkowski de un politopo convexo y de un cono poliédrico.[13][14] Los conos poliédricos también juegan un papel importante en la demostración del teorema de bases finitas para politopos, que demuestra que cada politopo es un poliedro y cada poliedro acotado es un politopo.[13][15][16]
Las dos representaciones de un cono poliédrico, mediante desigualdades y mediante vectores, pueden tener tamaños muy diferentes. Por ejemplo, considérese el cono de todas las matrices n-por-n no negativas con sumas iguales de filas y columnas. La representación de desigualdad requiere n2 desigualdades y ecuaciones 2(n − 1), pero la representación vectorial requiere n! vectores (véase teorema de Birkhoff-von Neumann). También puede ocurrir lo contrario: el número de vectores puede ser polinómico, mientras que el número de desigualdades es exponencial.[9]: 256
Las dos representaciones unidas proporcionan una forma eficaz de decidir si un vector dado está en el cono: para demostrar que está en el cono, basta con presentarlo como una combinación cónica de los vectores que lo definen; y para demostrar que no está en el cono, basta con presentar una única desigualdad definitoria que no cumpla. Este hecho se conoce como el lema de Farkas.
Un punto sutil en la representación por vectores es que el número de vectores puede ser exponencial en la dimensión, por lo que la prueba de que un vector está en el cono podría ser exponencialmente larga. Afortunadamente, el teorema de Carathéodory garantiza que cada vector en el cono puede representarse como máximo mediante d vectores que lo definen, donde d es la dimensión del espacio.
Conos romos, puntiagudos, planos, salientes y propios
editarSegún la definición anterior, si C es un cono convexo, entonces C ∪ {0} también es un cono convexo. Se dice que un cono convexo es puntiagudo si 0 está en C y romo si 0 no está en C.[1][17] Los conos romos se pueden excluir de la definición de cono convexo sustituyendo positivo por no negativo en la condición de α, β.
Un cono se llama plano si contiene algún vector distinto de cero x y su opuesto −x, lo que significa que C contiene un subespacio lineal de dimensión al menos uno, y saliente en caso contrario.[18][19] Un cono convexo romo es necesariamente saliente, pero lo contrario no es necesariamente cierto. Un cono convexo C es saliente si y solo si C ∩ −C ⊆ {0}. Se dice que un cono C es generador si es igual a todo el espacio vectorial. [20]
Algunos autores exigen que los conos salientes sean puntiagudos.[21] El término puntiagudo también se utiliza a menudo para referirse a un cono cerrado que no contiene una línea completa (es decir, ningún subespacio no trivial del espacio vectorial entorno V, o lo que se llama un cono saliente).[22][23][24] El término cono propio (convexo) se define de diversas formas, según el contexto y el autor. A menudo significa un cono que satisface otras propiedades como ser convexo, cerrado, puntiagudo, saliente y de dimensión completa.[25][26][27] Debido a estas diferentes definiciones, se debe consultar el contexto o la fuente para la definición de estos términos.
Conos racionales
editarUn tipo de cono de particular interés para los matemáticos puros es el conjunto parcialmente ordenado de los conos racionales. "Los conos racionales son objetos importantes en geometría algebraica tórica, álgebra conmutativa combinatoria, combinatoria geométrica y programación entera".[28] Este objeto surge cuando se estudian los conos en junto con el retículo . Un cono se llama racional (aquí se asume que es puntiagudo, como se definió anteriormente) siempre que todos sus generadores tengan coordenadas enteras, es decir, si es un cono racional, entonces .
Cono dual
editarSea C ⊂ V un conjunto, no necesariamente un conjunto convexo, en un espacio vectorial real V equipado con un producto interior. El cono dual (continuo o topológico) de C es el conjunto
que es siempre un cono convexo. Aquí, es el emparejamiento de dualidad entre C y V, es decir, .
De manera más general, el cono dual (algebraico) de C ⊂ V en un espacio lineal V es un subconjunto del espacio dual V* definido por:
En otras palabras, si V* es el espacio dual de V, C* es el conjunto de funcionales lineales que son no negativos en el cono primario C. Si se toma V* como espacio dual, entonces es el conjunto de funcionales lineales continuos no negativos en C.[29] Esta noción no requiere la especificación de un producto interno en V.
En dimensiones finitas, las dos nociones de cono dual son esencialmente la misma, porque cada funcional lineal de dimensión finita es continua,[30] y cada funcional lineal continuo en un espacio producto interno induce un isomorfismo lineal (mapa lineal no singular) de V* a V, y este isomorfismo llevará el cono dual dado por la segunda definición, en V*, al dado por la primera definición (véase el teorema de representación de Riesz).[29]
Si C es igual a su cono dual, entonces C es denominado auto-dual. Se puede decir que un cono es autodual sin referencia a ningún producto interno dado, si existe un producto interno con respecto al cual es igual a su dual según la primera definición.
Construcciones
editar- Dado un subconjunto cerrado y convexo K de un espacio de Hilbert V, el cono normal exterior al conjunto K en el punto x en K es dado por
- Dado un subconjunto cerrado y convexo K de V, el cono tangente (o cono contingente) al conjunto K en el punto x está dada por
- Dado un subconjunto cerrado y convexo K del espacio de Hilbert V, el cono tangente al conjunto K en el punto x en K se puede definir como el cono polar al cono normal hacia afuera :
Tanto el cono normal como el tangente tienen la propiedad de ser cerrados y convexos.
Son conceptos importantes en los campos de la optimización convexa, las desigualdades variacionales y los sistemas dinámicos proyectados.
Propiedades
editarSi C es un cono convexo no vacío en X, entonces el dominio lineal de C es igual a C - C y el subespacio vectorial más grande de X contenida en C es igual a C ∩ (−C).[31]
Orden parcial definido por un cono convexo
editarUn cono convexo puntiagudo y saliente C induce un conjunto parcialmente ordenado "≥" en V, definido de manera que si y solo si (si el cono es plano, la misma definición da simplemente un conjunto preordenado), y los múltiplos escalares positivos de desigualdades válidas con respecto a este orden siguen siendo desigualdades válidas. Un espacio vectorial con tal orden se llama espacio vectorial ordenado. Los ejemplos incluyen el orden del producto en vectores de valores reales, y el orden de Loewner en matrices semidefinidas positivas. Este orden se encuentra comúnmente en programación semidefinida.
Véase también
editarReferencias
editar- ↑ a b Bernstein, Dennis S. (26 de julio de 2009). Matrix Mathematics: Theory, Facts, and Formulas (en inglés) (Second edición). Princeton University Press. p. 97. ISBN 978-0691140391.
- ↑ C. Zalinescu (1 de enero de 2002). Convex Analysis in General Vector Spaces. World Scientific. p. 1. ISBN 978-981-238-067-8.
- ↑ Nef, Walter (1 de enero de 1988). Linear Algebra (en inglés). Courier Corporation. p. 35. ISBN 9780486657721.
- ↑ Itô, Kiyosi (1 de enero de 1993). Encyclopedic Dictionary of Mathematics (en inglés). MIT Press. ISBN 9780262590204.
- ↑ Rockafellar, Ralph Tyrell (29 de abril de 2015). Convex Analysis (en inglés). Princeton University Press. p. 13. ISBN 9781400873173.
- ↑ Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (6 de diciembre de 2012). Fundamentals of Convex Analysis (en inglés). Springer Science & Business Media. ISBN 9783642564680.
- ↑ Aliprantis, Charalambos D.; Border, Kim C. (2 de mayo de 2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (en inglés). Springer Science & Business Media. p. 197. ISBN 9783540326960.
- ↑ Rockafellar, Ralph Tyrell (29 de abril de 2015). Convex Analysis (en inglés). Princeton University Press. p. 10. ISBN 9781400873173.
- ↑ a b * Lovász, László; Plummer, M. D. (1986). Matching Theory. Annals of Discrete Mathematics (en inglés) 29. North-Holland. ISBN 0-444-87916-1. MR 0859549.
- ↑ a b Loera, Jesús A. De; Hemmecke, Raymond; Köppe, Matthias (1 de enero de 2012). Algebraic and Geometric Ideas in the Theory of Discrete Optimization (en inglés). SIAM. ISBN 9781611972443.
- ↑ Schrijver, Alexander (7 de julio de 1998). Theory of Linear and Integer Programming (en inglés). John Wiley & Sons. ISBN 9780471982326.
- ↑ Bruns, Winfried; Gubeladze, Joseph (2009). Polytopes, Rings and K-Theory (1 edición). Springer Monographs in Mathematics. p. 3. ISBN 9780387763552.
- ↑ a b Schrijver, Alexander (7 de julio de 1998). Theory of Linear and Integer Programming (en inglés). John Wiley & Sons. pp. 88-89. ISBN 9780471982326.
- ↑ Conforti, Michele; Cornuejols, Gerard; Zambelli, Giacomo (15 de noviembre de 2014). Integer Programming (en inglés). Springer. p. 111. ISBN 9783319110080.
- ↑ Korte, Bernhard; Vygen, Jens (11 de noviembre de 2013). Combinatorial Optimization: Theory and Algorithms (en inglés). Springer Science & Business Media. p. 61. ISBN 9783662217115.
- ↑ Villarreal, Rafael (26 de marzo de 2015). Monomial Algebras, Second Edition (en inglés). CRC Press. p. 9. ISBN 9781482234701.
- ↑ Dhara, Anulekha; Dutta, Joydeep (17 de octubre de 2011). Optimality Conditions in Convex Optimization: A Finite-Dimensional View (en inglés). CRC Press. p. 243. ISBN 9781439868225.
- ↑ Neustadt, Lucien W. (8 de marzo de 2015). Optimization: A Theory of Necessary Conditions (en inglés). Princeton University Press. p. 6. ISBN 9781400870530.
- ↑ Edwards, R. E. (25 de octubre de 2012). Functional Analysis: Theory and Applications (en inglés). Courier Corporation. p. 135. ISBN 9780486145105.
- ↑ Schaefer y Wolff, 1999, pp. 205–209.
- ↑ Hadjisavvas, Nicolas; Martinez-Legaz, Juan E.; Penot, Jean-Paul (10 de abril de 2001). Generalized Convexity and Generalized Monotonicity: Proceedings of the 6th International Symposium on Generalized Convexity/Monotonicity, Samos, September 1999 (en inglés). Springer Science & Business Media. p. 238. ISBN 9783540418061.
- ↑ Bauschke, Heinz H.; Combettes, Patrick L. (19 de abril de 2011). Convex Analysis and Monotone Operator Theory in Hilbert Spaces (en inglés). Springer Science & Business Media. p. 88. ISBN 9781441994677.
- ↑ Cameron, Neil (5 de septiembre de 1985). Introduction to Linear and Convex Programming (en inglés). CUP Archive. p. 32. ISBN 9780521312073.
- ↑ Panik, M. J. (1 de diciembre de 2013). Linear Programming: Mathematics, Theory and Algorithms (en inglés). Springer Science & Business Media. p. 40. ISBN 9781461334347.
- ↑ Dattorro, Jon (1 de enero de 2005). Convex Optimization & Euclidean Distance Geometry (en inglés). Meboo Publishing USA. p. 96. ISBN 9780976401308.
- ↑ Nicola, PierCarlo (14 de marzo de 2013). Mainstream Mathematical Economics in the 20th Century (en inglés). Springer Science & Business Media. p. 125. ISBN 9783662042380.
- ↑ Fujiwara, Hidenori; Ludwig, Jean (5 de diciembre de 2014). Harmonic Analysis on Exponential Solvable Lie Groups (en inglés). Springer. p. 246. ISBN 9784431552888.
- ↑ Gubeladze, Joseph; Michałek, Mateusz (1 de enero de 2018). «The poset of rational cones». Pacific Journal of Mathematics 292 (1): 103-115. S2CID 119639952. arXiv:1606.02083. doi:10.2140/pjm.2018.292.103.
- ↑ a b Hunter, John K.; Nachtergaele, Bruno (1 de enero de 2001). Applied Analysis (en inglés). World Scientific. p. 116. ISBN 9789810241919.
- ↑ Carothers, N. L. (1 de enero de 2005). A Short Course on Banach Space Theory (en inglés). Cambridge University Press. ISBN 9780521603720.
- ↑ Narici y Beckenstein, 2011, pp. 149-153.
Bibliografía
editar- Bourbaki, Nicolas (1987). Topological Vector Spaces. Elements of Mathematics. Berlin, New York: Springer Science+Business Media. ISBN 978-3-540-13627-9.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second edición). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Rockafellar, R. T. (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. ISBN 1-4008-7317-7.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM 8 (Second edición). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
- Zălinescu, C. (2002). Convex Analysis in General Vector Spaces. River Edge, NJ: World Scientific. ISBN 981-238-067-1. MR 1921556.

