Gran rombicuboctaedro no convexo
En geometría, el gran rombicuboctaedro no convexo es un poliedro uniforme estrellado, indexado como U17. Tiene 26 caras (8 triángulos y 18 cuadrados), 48 aristas y 24 vértices.[1] Está representado por el símbolo de Schläfli rr{4,3⁄2} y su diagrama de Coxeter-Dynkin es ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Su figura de vértice es un cuadrilátero cruzado.
. Su figura de vértice es un cuadrilátero cruzado.
| Gran rombicuboctaedro no convexo | ||
|---|---|---|
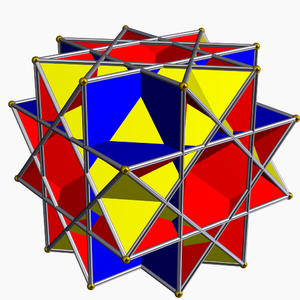 | ||
 Modelo 3D | ||
| Tipo |
poliedro uniforme y poliedro no convexo | |
| Forma de las caras |
triángulo equilátero (8) cuadrado (18) | |
| Configuración de vértices |
cuadrilátero | |
| Dual |
gran icositetraedro deltoidal | |
| Elementos | ||
| Vértices | 24 | |
| Aristas | 48 | |
| Caras | 26 | |
| Más información | ||
| MathWorld |
UniformGreatRhombicuboctahedron | |
Este modelo comparte el nombre con el gran rombicuboctaedro convexo, también llamado cuboctaedro truncado.
Un nombre alternativo para esta figura es cuasihombicuboctaedro. De ahí deriva su acrónimo de Bowers: querco.
Proyecciones ortográficas
editarCoordenadas cartesianas
editarLas coordenadas cartesianas de los vértices de un gran rombicuboctaedro no convexo centrado en el origen con longitud de arista 1 son todas las permutaciones de
- (±ξ, ±1, ±1),
donde ξ= √2 − 1.
Poliedros relacionados
editarComparte la disposición de vértices con el cubo truncado convexo. Además, comparte su disposición de vértices con el gran cubicuboctaedro (que tiene caras triangulares y 6 caras cuadradas en común) y con el gran rombihexaedro (que tiene 12 caras cuadradas en común). Posee la misma figura de vértice que el pseudo gran rombicuboctaedro, que no es un poliedro uniforme.
| Cubo truncado |
Gran rombicuboctaedro |
Gran cubicuboctaedro |
Gran rombihexaedro |
Pseudo gran rombicuboctaedro |
Gran icositetraedro deltoidal
editar| Gran icositetraedro deltoidal | ||
|---|---|---|
|
Imagen del sólido | ||
| Tipo | Poliedro estrellado | |
| Caras | 24 | |
| Aristas | 48 | |
| Vértices | 26 | |
| Grupo de simetría | Oh, [4,3], *432 | |
| Poliedro dual | Gran rombicuboctaedro no convexo | |
El gran icositetraedro deltoidal es el dual del gran rombicuboctaedro no convexo.
Referencias
editar- ↑ Maeder, Roman. «17: great rhombicuboctahedron». MathConsult.
Bibliografía
editar- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208, doi:10.1017/CBO9780511569371.
Enlaces externos
editarWeisstein, Eric W. «Great Deltoidal Icositetrahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Uniform great rhombicuboctahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Gran Rombicuboctaedro Modelo de papel