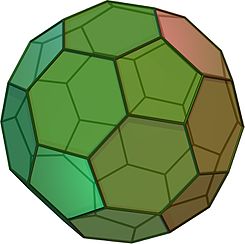
Icosaedro truncado
| Icosaedro Truncado | |
|---|---|
| |
| Grupo | Sólidos de Arquímedes |
| Número de caras | 32 |
| Polígonos que forman las caras | 12 Pentágonos 20 Hexágonos |
| Número de aristas | 90 |
| Número de vértices | 60 |
| Tipo de Vértice | Uniforme de Orden 3 |
| Caras relacionadas en los vértices | 2 Hexágonos 1 Pentágono |
| Simetría | Icosaédrica (Ih) |
| Poliedro dual | Pentaquisdodecaedro |
| Propiedades | Poliedro convexo, de vértices uniformes |
El icosaedro truncado es un sólido de Arquímedes que se obtiene truncando cada vértice de un icosaedro.
Propiedades generales
editarEn geometría, el icosaedro truncado es un sólido arquimediano, uno de los 13 sólidos no prismáticos isogonales convexos cuyas 32 caras son dos o más tipos de polígonos regulares. Es la única de estas formas que no contiene triángulos ni cuadrados. En el uso general, se supone que el grado de truncamiento es uniforme a menos que se especifique lo contrario.
Tiene 12 caras regulares pentagonales, 20 caras regulares hexagonales, 60 vértices y 90 aristas.
Es el poliedro de Goldberg GPV(1,1) o {5+,3}1,1, que contiene caras pentagonales y hexagonales.
Esta geometría está asociada con los balones de fútbol, habitualmente estampados con hexágonos blancos y pentágonos negros. Las cúpulas geodésicas, como aquellas en cuya arquitectura fue pionero Richard Buckminster Fuller, a menudo se basan en esta estructura. También corresponde a la geometría de la molécula del fullereno C60 ("buckybola").
Se utiliza en el teselado hiperbólico de llenado del espacio con una figura isoedral, el panal dodecaédrico bitruncado de orden-5.
Construcción
editarEste poliedro se puede construir a partir de un icosaedro con los 12 vértices truncados (cortados o seccionados) de modo que un tercio de cada arista se corta en cada uno de los dos extremos. Esto crea 12 nuevas caras pentagonales y deja las 20 caras triangulares originales como hexágonos regulares. Así, la longitud de los bordes es un tercio de la de los bordes originales. Además, la forma tiene 1440 diagonales interiores (cada vértice del icosaedro truncado está rodeado perimetralmente por otros 11 vértices, con los que no forma diagonales interiores; y tampoco forma una diagonal consigo mismo, luego cada vértice se puede combinar con otros 48 vértices (48=60-12); en consecuencia, el número de diagonales es el resultado de dividir por dos -la diagonal entre el vértice A y el B, es la misma que la diagonal entre el vértice B y el A- el producto de ambas cifras, de forma que 60·48/2=1440).
Características
editarEn geometría y en teoría de grafos, hay algunos poliedros característicos estándar.
Coordenadas cartesianas
editarLas coordenadas cartesianas para los vértices de un icosaedro truncado centrado en el origen son todas permutaciones pares:
- (0, ±1, ±3φ)
- (±1, ±(2 + φ), ±2φ)
- (±φ, ±2, ±(2φ + 1))
donde φ = 1 + √52 es el número áureo. El circunradio es √9φ + 10 ≈ 4.956 y las aristas tienen longitud 2.[1]
Proyecciones ortogonales
editarEl icosaedro truncado tiene cinco tipos de proyecciones ortogonales especiales centradas: en un vértice, en dos tipos de aristas y en dos tipos de caras (hexagonal y pentagonal). Las dos últimas corresponden a los planos de Coxeter A2 y H2.
| Centradas por | Vértice | Arista 5-6 |
Arista 6-6 |
Cara hexagonal |
Cara pentagonal |
|---|---|---|---|---|---|
| Sólido | |||||
| Alámbrico | |||||
| Simetría proyectiva |
[2] | [2] | [2] | [6] | [10] |
| Dual |
Teselado esférico
editarEl icosaedro truncado también se puede representar como un poliedro esférico y proyectarlo en un plano mediante una proyección estereográfica. Esta proyección es conforme, preservando los ángulos pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.
| Centrada en pentágono |
Centrada en hexágono | |
| Proyección ortogonal | Proyecciones estereográficas | |
|---|---|---|
Dimensiones
editarSi la longitud de la arista de un icosaedro truncado es a, el radio de una esfera circunscrita (una que toca el icosaedro truncado en todos los vértices) es:
donde φ es el número áureo.
Este resultado es fácil de obtener utilizando uno de los tres rectángulos áureos ortogonales dibujados en el icosaedro original (antes del corte) como punto de partida para las consideraciones realizadas. El ángulo entre los segmentos que unen el centro y los vértices conectados por el borde compartido (calculado sobre la base de esta construcción) es de aproximadamente 23,281446°.
Área y volumen
editarEl área A y el volumen V del icosaedro truncado de longitud de arista a son:
Con aristas unitarias, el área de la superficie (redondeada) es de 21 para los pentágonos y de 52 para los hexágonos, que suman 73 (véase áreas de polígonos regulares).
El icosaedro truncado muestra fácilmente la característica de Euler:
- 32 + 60 − 90 = 2.
Aplicaciones
editarLos balones de fútbol y los de balonmano son quizás el ejemplo más conocido de un poliedro esférico análogo al icosaedro truncado que se encuentra en la vida cotidiana.[2] Disponen del mismo patrón de pentágonos regulares y hexágonos regulares, pero adoptan una forma más esférica debido a la presión del aire en el interior y la elasticidad de la pelota. Este tipo de balones se introdujo en Copa Mundial de Fútbol de 1970 (a partir de 2006, este diseño icónico ha sido reemplazado por otros patrones).
Las señales de tráfico británicas que indican campos de fútbol utilizan una sección de teselado hexagonal de color uniforme para representar un balón de fútbol, en lugar de un icosaedro truncado. Esto enfureció al matemático y comediante Matt Parker, quien inició una petición al gobierno del Reino Unido para cambiar estos signos, de forma que fuesen geométricamente más precisos. La petición fue finalmente rechazada.
Las cúpulas geodésicas generalmente se basan en facetas triangulares de esta geometría, con estructuras que pueden servir de ejemplo distribuidas por todo el mundo, popularizadas por Richard Buckminster Fuller.[3]
Se utilizó una variación del icosaedro como base de las ruedas de nido de abeja (hechas de un material polifundido) utilizadas por la Pontiac Motor Division entre 1971 y 1976 en sus modelos Trans Am y Grand Prix.
Esta forma también fue la configuración de las lentes utilizadas para enfocar las ondas de choque explosivas de los detonadores de las primeras bombas atómicas, tanto en la prueba Trinity como en el diseño de la Fat Man.[4]
El icosaedro truncado también se puede describir como un modelo de la molécula del buckminsterfullereno (fullereno) (C60), o "buckybola", una alotropía de carbono elemental, descubierta en 1985. El diámetro de la pelota de fútbol y de la molécula de fullereno son 22 cm y aproximadamente 0,71 nm, respectivamente, por lo que la relación de tamaño es ≈31 000 000:1.
En la cultura artesanal popular, los sparkleballs grandes (pantallas de lámpara decorativas de forma esférica generalmente confeccionadas con materiales reutilizados) se pueden hacer usando un patrón de icosaedro truncado y vasos de plástico, espuma de poliestireno o papel.
En las artes
editar-
El icosaedro truncado (izquierda) comparado con un balón de fútbol
-
Molécula de fullereno C60
-
Icosaedro truncado mecanizado a partir de aluminio 6061
Poliedros relacionados
editar| Familia de poliedros icosaédricos uniformes | |||||||
|---|---|---|---|---|---|---|---|
| Simetría: [5,3], (*532) | [5,3]+, (532) | ||||||
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duales de los poliedros uniformes | |||||||
| Archivo:PentakisDodecahedron.svg | |||||||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| *n32 mutación simétrica de teselados truncados: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sim. *n42 [n,3] |
Esférico | Euclídeo | Compacto | Parac. | Hiperbólico no compacto | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Figuras truncadas |
||||||||||||
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis imágenes |
||||||||||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Estos poliedros uniformes estrellados y una estelación icosaédrica tienen una envolvente convexa de icosaedros truncados no uniformes:
| Poliedros en estrella uniformes con bases convexas de icosaedros truncados | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Este poliedro se parece al dodecaedro achaflanado uniforme, que también tiene 12 pentágonos pero que cuenta con 30 hexágonos.
Grafo icosaédrico truncado
editar| Grafo icosaédrico truncado | ||
|---|---|---|
| Vértices | 60 | |
| Aristas | 90 | |
| Automorfismos | 120 | |
| Número cromático | 3 | |
| Propiedades | Cúbico, hamiltoniano, regular, cero-simétrico | |
En el campo de la teoría de grafos, un grafo icosaédrico truncado es el esqueleto del icosaedro truncado, uno de los Sólidos arquimedianos. Tiene 60 vértices y 90 aristas, y es un grafo arquimediano cúbico.[5][6][7][8]
| 5-veces simétrica |
5-diagrama de Schlegel |
Historia
editarEl icosaedro truncado fue conocido por Arquímedes, quien clasificó los conocidos como 13 sólidos de Arquímedes en un trabajo perdido. Todo lo que se sabe de su trabajo sobre estas formas proviene de Papo de Alejandría, quien se limitó a enumerar el número de caras de cada una: 12 pentágonos y 20 hexágonos, en el caso del icosaedro truncado. La primera imagen conocida y descripción completa de un icosaedro truncado proviene de un redescubrimiento de Piero della Francesca, en su libro del siglo XV De quinque corporibus regularibus,[9], que incluía cinco de los sólidos de Arquímedes (los cinco truncamientos de los poliedros regulares). La misma forma fue representada por Leonardo da Vinci, en sus ilustraciones para el plagio de Luca Pacioli del libro de della Francesca en 1509. Aunque Alberto Durero omitió esta forma de los otros sólidos de Arquímedes enumerados en su libro de 1525 sobre poliedros, Underweysung der Messung, se encontró una descripción en sus artículos póstumos, publicados en 1538. Más adelante, Johannes Kepler redescubrió la lista completa de los 13 sólidos de Arquímedes, incluido el icosaedro truncado, y los incluyó en su libro de 1609, Harmonices mundi.[10]
Véase también
editarReferencias
editar- ↑ Weisstein, Eric W. «Icosahedral group». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Kotschick, Dieter (2006). «The Topology and Combinatorics of Soccer Balls». American Scientist 94 (4): 350-357. doi:10.1511/2006.60.350.
- ↑ Krebs, Albin (2 de julio de 1983). «R. Buckminster Fuller Dead; Futurist Built Geodesic Dome». The New York Times (New York, N.Y.). p. 1. Consultado el 7 de noviembre de 2021.
- ↑ Rhodes, Richard (1996). Dark Sun: The Making of the Hydrogen Bomb. Touchstone Books. pp. 195. ISBN 0-684-82414-0.
- ↑ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs. Oxford University Press. p. 268.
- ↑ Weisstein, Eric W. «Truncated icosahedral graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Godsil, C. and Royle, G. Algebraic Graph Theory New York: Springer-Verlag, p. 211, 2001
- ↑ Kostant, B. The Graph of the Truncated Icosahedron and the Last Letter of Galois. Notices Amer. Math. Soc. 42, 1995, pp. 959-968 PDF
- ↑ Katz, Eugene A. (2011). «Bridges between mathematics, natural sciences, architecture and art: case of fullerenes». Art, Science, and Technology: Interaction Between Three Cultures, Proceedings of the First International Conference. pp. 60-71.
- ↑ Field, J. V. (1997). «Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler». Archive for History of Exact Sciences 50 (3–4): 241-289. JSTOR 41134110. MR 1457069. S2CID 118516740. doi:10.1007/BF00374595.
Bibliografía
editar- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Sección 3-9)
- Cromwell, P. (1997). «Archimedean solids». Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468.
Enlaces externos
editar- Wikcionario tiene definiciones y otra información sobre icosaedro truncado.
- Weisstein, Eric W. «Truncated icosahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Truncated icosahedral graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Klitzing, Richard. «3D convex uniform polyhedra x3x5o - ti».
- Red imprimible editable de un icosaedro truncado con vista 3D interactiva
- Los poliedros uniformes
- "Polyhedra de Realidad Virtual"—La Enciclopedia de Poliedros
- Visualización de datos en papel 3D Balón de la Copa del Mundo Archivado el 18 de marzo de 2021 en Wayback Machine.