Lemniscata de Bernoulli
En geometría, la lemniscata de Bernoulli es una curva plana unicursal definida a partir de dos puntos dados F1 y F2, conocidos como focos, situados a una distancia de 2d entre sí, como el lugar geométrico de los puntos P tales que el producto de su distancia a los dos focos es constante y vale d2:
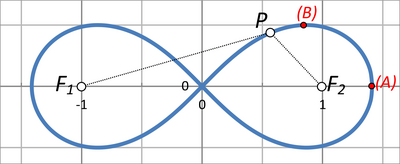
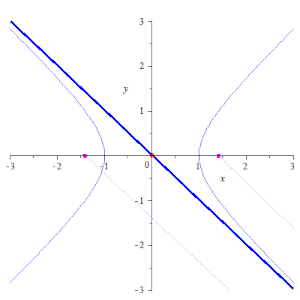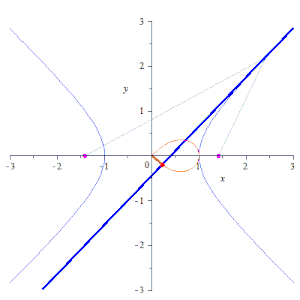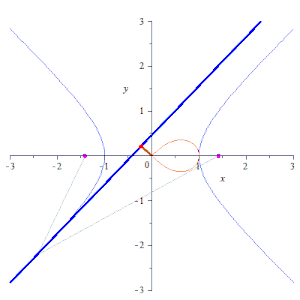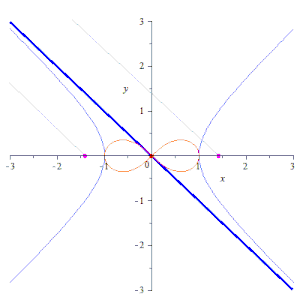

- PF1 · PF2 = d2
La curva posee una forma similar al número 8 y al símbolo del ∞. El símbolo del infinito en sí mismo es a veces llamado lemniscata. Su representación en Unicode es ∞, correspondiente al código (#8734).
Es tanto un caso especial del óvalo de Cassini como una curva algebraica racional de grado 4. Lleva el nombre del matemático y físico suizo Jakob Bernoulli.
Etimología
editarSu nombre en latín, lemniscatus, hace referencia a un objeto "decorado con cintas colgantes".[1] Jakob Bernoulli la redescubrió en 1694 durante su trabajo sobre la elipse,[2] y la llamó lemniscus.[3]
Historia
editarLa lemniscata de Bernoulli es parte de una familia de curvas descritas por Jean-Dominique Cassini en 1680, los óvalos de Cassini. Fue descrita por primera vez en 1694 por Jakob Bernoulli como una modificación de una elipse, (que es el lugar geométrico de los puntos para los que la suma de las distancias a cada uno de los dos "puntos focales" fijos es constante). Un óvalo de Cassini, por el contrario, es el lugar de los puntos para los que el producto de estas distancias es constante. En el caso de que la curva pase por el punto intermedio entre los dos focos, el óvalo es una lemniscata de Bernoulli.
El problema de la longitud de los arcos de la lemniscata fue tratado por Giulio Carlo de' Toschi di Fagnano en 1750. Halló el área limitada por esta curva y usó la figura de la lemniscata en la portada de su obra con la leyenda «Multifariam divisa atque dimensa. Deo veritatis gloria» (Dividida muchas veces y medida. Gloria al Dios de la verdad).[4]
Longitud de arco y funciones elípticas
editarLa determinación de la longitud de los arcos de la lemniscata conlleva al cálculo de una integral elíptica, como se descubrió en el siglo XVIII. Alrededor de 1800, las funciones elípticas implicadas en esas integrales fueron estudiadas por Carl Friedrich Gauss (en gran parte su trabajo no fue publicado en ese momento, pero dejó numerosas alusiones en las notas a su obra "Disquisitiones arithmeticae"). El par fundamental de períodos posee una forma muy especial y son proporcionales a enteros gaussianos. Por esta razón, el caso de las funciones elípticas con multiplicación compleja por la √−1 se denomina "caso lemniscático" en algunas publicaciones.
Usando la integral elíptica
se obtiene la fórmula de la longitud de arco como
- .
¿El símbolo del infinito?
editarUna opinión popular sostiene que la lemniscata de Bernoulli se considera el símbolo del infinito [∞] porque es una curva que se puede recorrer sin fin. Sin embargo, la invención del símbolo se atribuye al matemático John Wallis, contemporáneo de Bernoulli.[5]
Generación gráfica
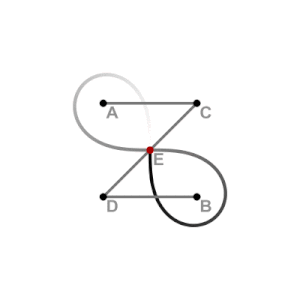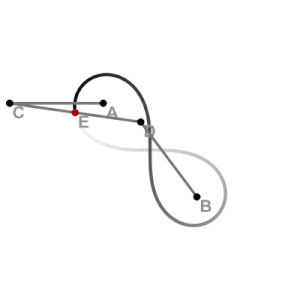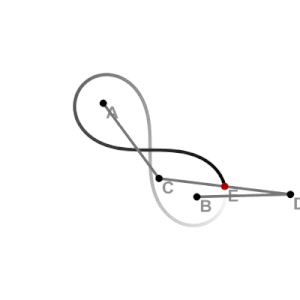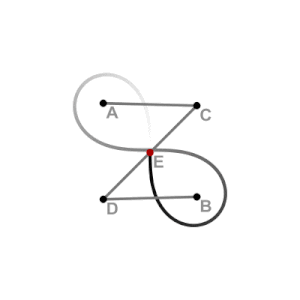
editarEsta curva se puede obtener como la inversión de una hipérbola equilátera, situando la circunferencia que define la inversión con su centro coincidente con el centro de la hipérbola (el punto medio de sus dos focos). También puede dibujarse con un acoplamiento mecánico en forma de mecanismo de Watt, con las longitudes de las tres barras del enlace y la distancia entre sus puntos finales elegidos para formar un cuadrado antiparalelogramo.[6]
Ecuaciones
editar- Su ecuación en coordenadas cartesianas es (excluidas traslación y rotación):
- Su ecuación explícita es:
- Su ecuación en el plano complejo es:
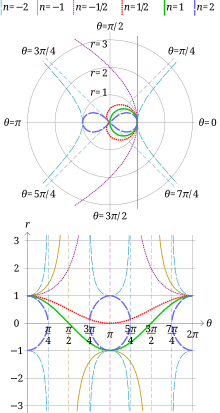
- En coordenadas polares:
- Como ecuación paramétrica:
- En coordenadas bicéntricas:
- En coordenadas polares:
Derivadas
editarSe calculan diferenciando la función implícita
|
|
Propiedades
editarEjes
editarPara una lemniscata con distancia desde un foco al origen, se tiene que:
- (semieje horizontal)
- (semieje vertical)
Área
editarEl área delimitada por la lemniscata de Bernoulli es:[7]
Cuadratura de la lemniscata: imposible para el círculo, la cuadratura exacta es posible para la lemniscata de Bernoulli. Su área de hecho coincide con la de dos cuadrados iguales, cuyo lado es la distancia entre un foco y el centro de la lemniscata.[nota 1] Esta área también es igual al área de un cuadrado cuyo lado es la distancia que separa el centro de un máximo de la lemniscata.
Longitud
editarLa longitud de la lemniscata de Bernoulli es:
donde M(u, v) es la media aritmético-geométrica de dos números u y v, es una integral elíptica de primera especie y Γ es la función gamma.
Ángulos
editarEl siguiente teorema sobre los ángulos de la lemniscata se debe al matemático alemán Gerhard Christoph Hermann Vechtmann, quien lo describió en 1843 en su disertación sobre las lemniscatas.[8]
- F1 y F2 son los focos de la lemniscata, O es el punto medio del segmento F1F2 y P es cualquier punto de la lemniscata fuera de la línea que conecta F1 y F2. La normal n de la lemniscata en P cruza la línea que conecta F1 y F2 en R. Ahora, el ángulo interior del triángulo OPR en O es un tercio del ángulo exterior del triángulo en R. Además, el ángulo interior en P es dos veces el ángulo interior en O.
Radio de curvatura
editarEl radio de curvatura es
siendo el radio de la expresión de la curva en coordenadas polares.
Otras propiedades
editar- La lemniscata solo tiene dos focos, siendo 2d la distancia entre ellos.[9]
- La lemniscata es simétrica a la línea que conecta sus focos F1 y F2 y también a la mediatriz del segmento de línea F1F2.
- La lemniscata es simétrica con respecto al punto medio del segmento F1F2.
- La lemniscata es la inversión de una hipérbola y viceversa.
- Las dos tangentes en el punto medio O son ortogonales y cada una de ellas forma un ángulo de con una línea que conecta F1 y F2.
- La sección transversal plana de un toro estándar tangente a su ecuador interno es una lemniscata.
- El matemático italiano Gian Francesco Malfatti descubrió que una bola que rueda sobre un arco de lemniscata bajo la influencia de la gravedad, tardará el mismo tiempo en descender que una bola que recorra el segmento rectilíneo que conecta los puntos extremos del arco.
Demostraciones
editarNOTA:
- En las demostraciones siguientes, se utiliza una notación ligeramente distinta, para adaptarse a la rotulación de los gráficos. Los focos F1 y F2 pasan a denominarse F' y F, y los puntos P de la curva, se designan como M.
Como ya se ha señalado, una lemniscata de Bernoulli es el conjunto de puntos M que verifican la relación:
donde F y F′ son dos puntos fijos y O su punto medio. Los puntos F y F′ se denominan focos de la lemniscata, y O es su centro.
Alternativamente, se puede definir una lemniscata de Bernoulli como el conjunto de puntos M que satisfacen la relación:
| Demostración |
La primera relación se llama "ecuación bipolar", y la segunda "ecuación tripolar".
La curva así definida pertenece a la familia de las lemniscatas (curvas en forma de 8), de las cuales es el ejemplo más conocido y el más rico en propiedades. Por su definición, es el ejemplo más notable de óvalo de Cassini. También representa la sección de un toro particular por un plano tangente a su ecuador interior.
Relación entre las ecuaciones en diferentes sistemas de coordenadas
editarMediante la semidistancia focal OF=d
editarSea OF = d. En coordenadas polares (el eje polar es OF), la lemniscata de Bernoulli admite la ecuación:
| Demostración |
En coordenadas cartesianas (el eje x es OF), y la lemniscata de Bernoulli se define según la ecuación (implícita):
| Demostración |
La abscisa x describe el intervalo (los límites se alcanzan para y = 0). La ordenada y describe el intervalo (los límites se alcanzan para ).
Es posible relacionar y de acuerdo con x:
| Demostración |
pero generalmente es más conveniente manipular la ecuación implícita que usar esta expresión explícita de y.
Representaciones paramétricas
editarPartiendo de la ecuación en coordenadas polares ρ2 = 2d2cos2θ, se puede representar la lemniscata de Bernoulli mediante las dos ecuaciones siguientes, tomando como parámetro el ángulo polar θ:
| Demostración |
Sin embargo, esta representación tiene el defecto de que, una vez finalizado el proceso, es necesario variar θ de –π/4 a +π/4 y luego de 5π/4 a 3π/4, una variación que no es continua ni monótona.
Una mejor representación paramétrica viene dada por:
| Demostración |
La lemniscata se recorre una vez variando φ de –π a +π. El parámetro φ está conectado directamente al ángulo polar por la relación cosφ = tanθ, o θ = arctan(cosφ).
También se puede convertir la representación anterior, trigonométrica, en una representación paramétrica racional:
| Demostración |
La lemniscata se recorre una vez variando t de –∞ a +∞. El parámetro t está directamente relacionado con el ángulo φ por la relación t = tan(φ/2).
Mediante el semieje OA = a
editarLa mayoría de las ecuaciones anteriores son un poco más simples y más naturales si se utiliza (semieje de la lemniscata).
En coordenadas polares (siendo el eje polar OA), la lemniscata de Bernoulli admite la ecuación:
En coordenadas cartesianas (el eje x es OA), la lemniscata de Bernoulli tiene como ecuación implícita:
La abscisa x describe el intervalo [–a, a] (los límites se alcanzan para y = 0). La ordenada y describe el intervalo (los límites se alcanzan para ). La longitud focal media es
Es posible expresar y de acuerdo con x:
pero generalmente es más conveniente manipular la ecuación implícita que usar esta expresión explícita de y.
Curvas de la misma familia
editarLa lemniscata de Bernoulli es un caso especial de óvalo de Cassini, hipopoda, espiral sinusoidal y de la spira de Perseo.
Aplicaciones
editarLa dinámica en esta curva y sus versiones más generalizadas se estudian en modelos quasi unidimensionales.
Véase también
editarNotas
editar- ↑ Esta distancia OF = OF' es también igual al diámetro de Féret pequeño de la lemniscata, es decir, su grosor perpendicular a la dirección F'OF.
Referencias
editar- ↑ N.V. Alexándrova. Diccionario Histórico de notaciones, términos y conceptos de las matemáticas ISBN 978-5-396-00676-8, se distribuye en el Perú.
- ↑ Weisstein, Eric W. «Lemniscate». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research..
- ↑ Hofmann: Historia de la matemática, Limusa. Noriega editores, México (2003) pág. 233
- ↑ N.V. Alexándrova. Diccionario Histórico de notaciones, términos y conceptos de las matemáticas ISBN 978-5-396-00676-8.
- ↑ John Wallis, De sectionibus conicis nova methodo expositis tractatus (1655), section I, Prop.1, p. 4.
- ↑ Bryant, John; Sangwin, Christopher J. (2008), How round is your circle? Where Engineering and Mathematics Meet, Princeton University Press, pp. 58-59, ISBN 978-0-691-13118-4..
- ↑ Maynard Kong. Cálculo integral ISBN 9789972421952
- ↑ Alexander Ostermann, Gerhard Wanner: Geometry by Its History. Springer, 2012, pp. 207-208
- ↑ "Geometría Analítica" (1968) Rey Pastor, Julio; Santaló, Luis; Balanzat, Manuel. Sin ISBN. pág. 195
Bibliografía
editar- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 4–5,121–123,145,151,184. ISBN 0-486-60288-5.
Enlaces externos
editar- Wikimedia Commons alberga una categoría multimedia sobre Lemniscata de Bernoulli.
- Weisstein, Eric W. «Lemniscate». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- "Lemniscate of Bernoulli" en The MacTutor History of Mathematics archive
- "Lemniscate of Bernoulli" (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). en MathCurve.
- Coup d'œil sur la lemniscata de Bernoulli (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). (en francés)
- Una mirada al lemniscata de Bernoulli, en el sitio del CNRS (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..
- Lemniscate de Bernoulli, en MathCurve (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..


