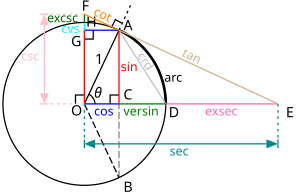
Todas las funciones en O Una identidad trigonométrica es una igualdad que vincula dos funciones trigonométricas y es válida en el dominio común o descartando los puntos que anulan alguna función en caso de ser divisor. Las funciones están ligadas por operaciones racionales y por potencias de exponente entero, aunque en algunos casos se recurre a la raíz cuadrada. Los ángulos se suman algebraicamente, se multiplican o se dividen por enteros positivos y luego actúan como argumento de alguna función.
Nota: la notación
sen
2
α
{\displaystyle \operatorname {sen} ^{2}\alpha }
(
sen
α
)
2
{\displaystyle (\operatorname {sen} \alpha )^{2}}
editar
Identidades trigonométricas fundamentales, y cómo convertir de una función trigonométrica a otra
sen
θ
=
y
,
cos
θ
=
x
{\displaystyle \operatorname {sen} \theta =y{\text{, }}\cos \theta =x}
Δ
R
{\displaystyle \Delta R}
x
{\displaystyle x}
y
{\displaystyle y}
θ
.
{\displaystyle \theta .}
tg
θ
=
sen
θ
cos
θ
,
θ
≠
π
2
+
π
k
p
a
r
a
k
∈
Z
.
{\displaystyle \operatorname {tg} \theta ={\frac {\operatorname {sen} \theta }{\cos \theta }},{\text{ }}\theta \neq {\frac {\pi }{2}}+\pi k\quad \mathrm {para} \quad k\in \mathbb {Z} .}
cot
θ
=
cos
θ
sen
θ
,
θ
≠
π
k
p
a
r
a
k
∈
Z
.
{\displaystyle \cot \theta ={\frac {\cos \theta }{\operatorname {sen} \theta }},{\text{ }}\theta \neq \pi k\quad \mathrm {para} \quad k\in \mathbb {Z} .}
sec
θ
=
1
cos
θ
,
θ
≠
π
2
+
π
k
,
p
a
r
a
k
∈
Z
.
{\displaystyle \sec \theta ={\frac {1}{\cos \theta }},{\text{ }}\theta \neq {\frac {\pi }{2}}+\pi k,\quad \mathrm {para} \quad k\in \mathbb {Z} .}
csc
θ
=
1
sen
θ
,
θ
≠
π
k
,
p
a
r
a
k
∈
Z
.
{\displaystyle \csc \theta ={\frac {1}{\operatorname {sen} \theta }},{\text{ }}\theta \neq \pi k,\quad \mathrm {para} \quad k\in \mathbb {Z} .}
[ 1]
Periodicidad
2
π
{\displaystyle 2\pi }
cos
θ
=
sen
(
π
2
+
θ
)
{\displaystyle \cos \theta =\operatorname {sen} \left({\frac {\pi }{2}}+\theta \right)}
Simetría
sen
θ
=
−
sen
(
−
θ
)
{\displaystyle \operatorname {sen} \theta =-\operatorname {sen}(-\theta )}
Relación pitagórica
sen
2
θ
+
cos
2
θ
=
1
{\displaystyle \operatorname {sen} ^{2}\theta +\cos ^{2}\theta =1\,}
Identidad de la razón
tg
θ
=
sen
θ
cos
θ
{\displaystyle \operatorname {tg} \theta ={\frac {\operatorname {sen} \theta }{\cos \theta }}}
De estas identidades, se puede elaborar la siguiente tabla. Para obtener el signo correcto en algunos casos se necesitará saber los valores para los cuales la función trigonométrica en cuestión es negativa o positiva.
Funciones trigonométricas en función de las otras cinco[ 2]
En términos de
sen
{\displaystyle \operatorname {sen} }
cos
{\displaystyle \cos }
tg
{\displaystyle \operatorname {tg} }
cot
{\displaystyle \cot }
sec
{\displaystyle \sec }
csc
{\displaystyle \csc }
sen
θ
{\displaystyle \operatorname {sen} \theta }
sen
θ
{\displaystyle \operatorname {sen} \theta }
cos
(
3
π
2
+
θ
)
{\displaystyle \cos \left({\frac {3\pi }{2}}+\theta \right)}
tg
θ
1
+
tg
2
θ
{\displaystyle {\frac {\operatorname {tg} \theta }{\sqrt {1+\operatorname {tg} ^{2}\theta }}}}
1
1
+
cot
2
θ
{\displaystyle {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}}
sec
2
θ
−
1
sec
θ
{\displaystyle {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}}
1
csc
θ
{\displaystyle {\frac {1}{\csc \theta }}}
cos
θ
{\displaystyle \cos \theta }
sen
(
π
2
+
θ
)
{\displaystyle \operatorname {sen} \left({\frac {\pi }{2}}+\theta \right)}
cos
θ
{\displaystyle \cos \theta \ }
1
1
+
tg
2
θ
{\displaystyle {\frac {1}{\sqrt {1+\operatorname {tg} ^{2}\theta }}}}
cot
θ
1
+
cot
2
θ
{\displaystyle {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}}
1
sec
θ
{\displaystyle {\frac {1}{\sec \theta }}}
csc
2
θ
−
1
csc
θ
{\displaystyle {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}}
tg
θ
{\displaystyle \operatorname {tg} \theta }
sen
θ
sen
(
π
2
+
θ
)
{\displaystyle {\frac {\operatorname {sen} \theta }{\operatorname {sen} \left({\frac {\pi }{2}}+\theta \right)}}}
cos
(
3
π
2
+
θ
)
cos
θ
{\displaystyle {\frac {\cos \left({\frac {3\pi }{2}}+\theta \right)}{\cos \theta }}}
tg
θ
{\displaystyle \operatorname {tg} \theta \ }
1
cot
θ
{\displaystyle {\frac {1}{\cot \theta }}}
sec
2
θ
−
1
{\displaystyle {\sqrt {\sec ^{2}\theta -1}}}
1
csc
2
θ
−
1
{\displaystyle {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}}
cot
θ
{\displaystyle \cot \theta }
sen
(
π
2
+
θ
)
sen
θ
{\displaystyle {\frac {\operatorname {sen} \left({\frac {\pi }{2}}+\theta \right)}{\operatorname {sen} \theta }}}
cos
θ
cos
(
3
π
2
+
θ
)
{\displaystyle {\frac {\cos \theta }{\cos \left({\frac {3\pi }{2}}+\theta \right)}}}
1
tg
θ
{\displaystyle {\frac {1}{\operatorname {tg} \theta }}}
cot
θ
{\displaystyle \cot \theta \ }
1
sec
2
θ
−
1
{\displaystyle {1 \over {\sqrt {\sec ^{2}\theta -1}}}}
csc
2
θ
−
1
{\displaystyle {\sqrt {\csc ^{2}\theta -1}}}
sec
θ
{\displaystyle \sec \theta }
1
sen
(
π
2
+
θ
)
{\displaystyle {\frac {1}{\operatorname {sen} \left({\frac {\pi }{2}}+\theta \right)}}}
1
cos
θ
{\displaystyle {\frac {1}{\cos \theta }}}
1
+
tg
2
θ
{\displaystyle {\sqrt {1+\operatorname {tg} ^{2}\theta }}}
1
+
cot
2
θ
cot
θ
{\displaystyle {{\sqrt {1+\cot ^{2}\theta }} \over \cot \theta }}
sec
θ
{\displaystyle \sec \theta \ }
csc
θ
csc
2
θ
−
1
{\displaystyle {\csc \theta \over {\sqrt {\csc ^{2}\theta -1}}}}
csc
θ
{\displaystyle \csc \theta }
1
sen
θ
{\displaystyle {\frac {1}{\operatorname {sen} \theta }}}
1
cos
(
3
π
2
+
θ
)
{\displaystyle {\frac {1}{\cos \left({\frac {3\pi }{2}}+\theta \right)}}}
1
+
tg
2
θ
tg
θ
{\displaystyle {{\sqrt {1+\operatorname {tg} ^{2}\theta }} \over \operatorname {tg} \theta }}
1
+
cot
2
θ
{\displaystyle {\sqrt {1+\cot ^{2}\theta }}}
sec
θ
sec
2
θ
−
1
{\displaystyle {\sec \theta \over {\sqrt {\sec ^{2}\theta -1}}}}
csc
θ
{\displaystyle \csc \theta \ }
De las definiciones de las funciones trigonométricas:
tg
x
=
sen
x
cos
x
cot
x
=
1
tg
x
=
cos
x
sen
x
{\displaystyle \operatorname {tg} {x}={\frac {\operatorname {sen} {x}}{\cos {x}}}\qquad \cot {x}={\frac {1}{\operatorname {tg} {x}}}={\frac {\cos {x}}{\operatorname {sen} {x}}}}
sec
x
=
1
cos
x
csc
x
=
1
sen
x
{\displaystyle \sec {x}={\frac {1}{\cos {x}}}\qquad \csc {x}={\frac {1}{\operatorname {sen} {x}}}}
Son más sencillas de probar en la circunferencia trigonométrica o goniométrica (que tiene radio igual a 1):
sen
(
x
)
=
sen
(
x
+
2
π
)
cos
(
x
)
=
cos
(
x
+
2
π
)
tg
(
x
)
=
tg
(
x
+
π
)
{\displaystyle \operatorname {sen}(x)=\operatorname {sen}(x+2\pi )\qquad \cos(x)=\cos(x+2\pi )\qquad \operatorname {tg} (x)=\operatorname {tg} (x+\pi )}
sen
(
−
x
)
=
sen
(
x
+
π
)
cos
(
−
x
)
=
−
cos
(
x
+
π
)
{\displaystyle \operatorname {sen}(-x)=\operatorname {sen}(x+\pi )\qquad \cos(-x)=-\cos(x+\pi )}
tg
(
−
x
)
=
−
tg
(
x
)
cot
(
−
x
)
=
−
cot
(
x
)
{\displaystyle \operatorname {tg} (-x)=-\operatorname {tg} (x)\qquad \cot(-x)=-\cot(x)}
sen
(
x
)
=
cos
(
π
2
−
x
)
cos
(
x
)
=
sen
(
π
2
−
x
)
tg
(
x
)
=
cot
(
π
2
−
x
)
{\displaystyle \operatorname {sen}(x)=\cos \left({\frac {\pi }{2}}-x\right)\qquad \cos(x)=\operatorname {sen} \left({\frac {\pi }{2}}-x\right)\qquad \operatorname {tg} (x)=\cot \left({\frac {\pi }{2}}-x\right)}
A veces es importante saber que cualquier combinación lineal de una serie de ondas senoidales que tienen el mismo período pero están desfasadas, es también una onda senoidal del mismo período pero con un desplazamiento de fase diferente. Dicho de otro modo:
a
sen
(
x
)
+
b
cos
(
x
)
=
a
2
+
b
2
⋅
sen
(
x
+
φ
)
{\displaystyle a\operatorname {sen}(x)+b\cos(x)={\sqrt {a^{2}+b^{2}}}\cdot \operatorname {sen} \left(x+\varphi \right)}
donde
φ
=
a
r
c
t
a
n
(
b
/
a
)
{\displaystyle \varphi ={\rm {arctan}}(b/a)}
φ
=
a
r
c
t
a
n
(
b
/
a
)
+
π
{\displaystyle \varphi ={\rm {arctan}}(b/a)+\pi }
Usando la función Atan2 también puede escribirse como
a
sen
(
x
)
+
b
cos
(
x
)
=
a
2
+
b
2
⋅
sen
(
x
+
atan2
(
b
,
a
)
)
{\displaystyle a\operatorname {sen}(x)+b\cos(x)={\sqrt {a^{2}+b^{2}}}\cdot \operatorname {sen} \left(x+\operatorname {atan2} (b,a)\right)}
La identidad
sen
2
(
x
)
+
cos
2
(
x
)
=
1
{\displaystyle \operatorname {sen} ^{2}\left(x\right)+\cos ^{2}\left(x\right)=1}
Es llamada identidad trigonométrica fundamental , y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros de "sen² + cos² = 1" por cos², se obtiene:
tg
2
(
x
)
+
1
=
sec
2
(
x
)
{\displaystyle \operatorname {tg} ^{2}\left(x\right)+1=\sec ^{2}\left(x\right)}
Ahora, dividiendo ambos miembros de la misma expresión por el sen², se obtiene:
cot
2
(
x
)
+
1
=
csc
2
(
x
)
{\displaystyle \cot ^{2}\left(x\right)+1=\csc ^{2}\left(x\right)}
Entonces puede expresarse la función seno según alguna otra conocida:
sen
(
x
)
=
1
−
cos
2
(
x
)
sen
(
x
)
=
tg
x
1
+
tg
2
(
x
)
{\displaystyle \operatorname {sen}(x)={\sqrt {1-\cos ^{2}(x)}}\qquad \operatorname {sen}(x)={\frac {\operatorname {tg} {x}}{\sqrt {1+\operatorname {tg} ^{2}(x)}}}}
sen
(
x
)
=
1
1
+
cot
2
(
x
)
sen
(
x
)
=
1
sec
x
sec
2
(
x
)
−
1
{\displaystyle \operatorname {sen}(x)={\frac {1}{\sqrt {1+\cot ^{2}(x)}}}\qquad \operatorname {sen}(x)={\frac {1}{\sec {x}}}{\sqrt {\sec ^{2}(x)-1}}}
Ejemplo 2 :
sec
2
t
−
1
sec
2
t
=
sen
2
t
{\displaystyle {\frac {\sec ^{2}t-1}{\sec ^{2}t}}=\operatorname {sen} ^{2}t}
sec
2
t
−
1
sec
2
t
=
{\displaystyle {\frac {\sec ^{2}t-1}{\sec ^{2}t}}=}
1
cos
2
t
−
1
1
cos
2
t
=
{\displaystyle {\frac {{\frac {1}{\cos ^{2}t}}-1}{\frac {1}{\cos ^{2}t}}}=}
cos
2
t
(
1
cos
2
t
−
1
)
=
{\displaystyle \cos ^{2}t\left({\frac {1}{\cos ^{2}t}}-1\right)=}
cos
2
t
(
1
−
cos
2
t
cos
2
t
)
=
{\displaystyle \cos ^{2}t\left({\frac {1-\cos ^{2}t}{\cos ^{2}t}}\right)=}
1
−
cos
2
t
=
{\displaystyle 1-\cos ^{2}t=}
sen
2
t
.
{\displaystyle \operatorname {sen} ^{2}t.}
editar
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
Las siguientes demostraciones son válidas sólo para valores de
α
,
β
∈
(
0
,
π
2
)
{\displaystyle \alpha ,\beta \in \left(0,{\frac {\pi }{2}}\right)}
A continuación se presenta una demostración válida para cualquier ángulo a partir de las definiciones de seno y coseno de cualquier ángulo como parametrizaciones del círculo unidad . Como lemas, se demuestra también que
cos
(
−
x
)
=
cos
(
x
)
{\displaystyle \cos(-x)=\cos(x)}
sin
(
−
x
)
=
−
sin
(
x
)
{\displaystyle \sin(-x)=-\sin(x)}
cos
(
π
2
−
x
)
=
sin
(
x
)
{\displaystyle \cos \left({\frac {\pi }{2}}-x\right)=\sin(x)}
Demostración para cualquier ángulo real.
Consideremos el círculo unidad
S
{\displaystyle S}
P
=
(
1
,
0
)
,
X
=
(
cos
x
,
sin
x
)
∈
S
{\displaystyle P=(1,0),X=(\cos x,\sin x)\in S}
x
∈
R
{\displaystyle x\in \mathbb {R} }
d
(
P
,
X
)
2
=
(
1
−
cos
x
)
2
+
(
0
−
sin
x
)
2
=
1
−
2
cos
x
+
cos
2
x
+
sin
2
x
=
1
−
2
cos
x
+
1
=
2
−
2
cos
x
{\displaystyle \operatorname {d} (P,X)^{2}=(1-\cos x)^{2}+(0-\sin x)^{2}=1-2\cos x+\cos ^{2}x+\sin ^{2}x=1-2\cos x+1=2-2\cos x}
Ahora consideremos
x
,
y
∈
R
{\displaystyle x,y\in \mathbb {R} }
X
=
(
cos
x
,
sin
x
)
,
Y
=
(
cos
y
,
sin
y
)
∈
S
{\displaystyle X=(\cos x,\sin x),Y=(\cos y,\sin y)\in S}
(
a
)
{\displaystyle (a)}
d
(
X
,
Y
)
2
=
(
cos
y
−
cos
x
)
2
+
(
sin
y
−
sin
x
)
2
=
cos
2
y
+
cos
2
x
−
2
cos
y
cos
x
+
sin
2
y
+
sin
2
x
−
2
sin
y
sin
x
=
2
−
2
cos
y
cos
x
−
2
sin
y
sin
x
{\displaystyle \operatorname {d} (X,Y)^{2}=(\cos y-\cos x)^{2}+(\sin y-\sin x)^{2}=\cos ^{2}y+\cos ^{2}x-2\cos y\cos x+\sin ^{2}y+\sin ^{2}x-2\sin y\sin x=2-2\cos y\cos x-2\sin y\sin x}
(
b
)
{\displaystyle (b)}
Hacemos la siguiente transformación en el plano: lo giramos alrededor del centro del círculo unidad
S
{\displaystyle S}
−
y
{\displaystyle -y}
Y
↦
P
=
(
1
,
0
)
{\displaystyle Y\mapsto P=(1,0)}
X
↦
X
′
:=
(
cos
(
x
−
y
)
,
sin
(
x
−
y
)
)
{\displaystyle X\mapsto X':=(\cos(x-y),\sin(x-y))}
d
(
Y
,
X
)
2
=
d
(
P
,
X
′
)
2
=
2
−
2
cos
(
x
−
y
)
{\displaystyle \operatorname {d} (Y,X)^{2}=\operatorname {d} (P,X')^{2}=2-2\cos(x-y)}
Igualamos ahora las expresiones encontradas en
(
a
)
{\displaystyle (a)}
(
b
)
{\displaystyle (b)}
2
−
2
cos
(
x
−
y
)
=
(
a
)
d
(
Y
,
X
)
2
=
(
b
)
2
−
2
cos
y
cos
x
−
2
sin
y
sin
x
⇒
cos
(
x
−
y
)
=
cos
x
cos
y
+
sin
x
sin
y
{\displaystyle 2-2\cos(x-y){\overset {(a)}{=}}\operatorname {d} (Y,X)^{2}{\overset {(b)}{=}}2-2\cos y\cos x-2\sin y\sin x\Rightarrow \cos(x-y)=\cos x\cos y+\sin x\sin y}
Esto demuestra la fórmula para el coseno de la resta, a la que nos referiremos en adelante como
(
∗
)
{\displaystyle (*)}
Lema
(
1
)
:
cos
(
π
2
−
x
)
=
sin
x
∀
x
∈
R
{\displaystyle {\text{Lema }}(1):\cos \left({\frac {\pi }{2}}-x\right)=\sin x\quad \forall x\in \mathbb {R} }
Es consecuencia directa de evaluar
(
∗
)
{\displaystyle (*)}
x
=
π
2
{\displaystyle x={\frac {\pi }{2}}}
Lema
(
2
)
:
cos
(
−
x
)
=
cos
x
∀
x
∈
R
{\displaystyle {\text{Lema }}(2):\cos(-x)=\cos x\quad \forall x\in \mathbb {R} }
Es consecuencia directa de evaluar
(
∗
)
{\displaystyle (*)}
x
=
0
{\displaystyle x=0}
Lema
(
3
)
:
sin
(
−
x
)
=
−
sin
x
∀
x
∈
R
{\displaystyle {\text{Lema }}(3):\sin(-x)=-\sin x\quad \forall x\in \mathbb {R} }
Por
(
∗
)
{\displaystyle (*)}
sin
(
−
x
)
=
(
1
)
cos
(
π
2
−
(
−
x
)
)
=
cos
(
π
2
+
x
)
=
(
2
)
cos
(
−
(
π
2
+
x
)
)
=
cos
(
−
π
2
−
x
)
=
(
∗
)
cos
x
cos
(
−
π
2
)
+
sin
x
sin
(
−
π
2
)
=
−
sin
x
{\displaystyle \sin(-x){\overset {(1)}{=}}\cos \left({\frac {\pi }{2}}-(-x)\right)=\cos \left({\frac {\pi }{2}}+x\right){\overset {(2)}{=}}\cos \left(-\left({\frac {\pi }{2}}+x\right)\right)=\cos \left(-{\frac {\pi }{2}}-x\right){\overset {(*)}{=}}\cos x\cos \left(-{\frac {\pi }{2}}\right)+\sin x\sin \left(-{\frac {\pi }{2}}\right)=-\sin x}
Con estos lemas vemos el resto de fórmulas:
cos
(
x
+
y
)
=
cos
(
x
−
(
−
y
)
)
=
(
∗
)
cos
x
cos
(
−
y
)
+
sin
x
sin
(
−
y
)
=
(
2
)
,
(
3
)
cos
x
cos
y
−
sin
x
sin
y
{\displaystyle \cos(x+y)=\cos(x-(-y)){\overset {(*)}{=}}\cos x\cos(-y)+\sin x\sin(-y){\overset {(2),(3)}{=}}\cos x\cos y-\sin x\sin y}
sin
(
x
−
y
)
=
(
1
)
cos
(
π
2
+
y
−
x
)
=
(
∗
)
cos
(
π
2
+
y
)
cos
x
+
sin
(
π
2
+
y
)
sin
x
=
(
1
)
{\displaystyle \sin(x-y){\overset {(1)}{=}}\cos \left({\frac {\pi }{2}}+y-x\right){\overset {(*)}{=}}\cos \left({\frac {\pi }{2}}+y\right)\cos x+\sin \left({\frac {\pi }{2}}+y\right)\sin x{\overset {(1)}{=}}}
=
sin
(
−
y
)
cos
x
+
cos
(
π
2
−
π
2
−
y
)
sin
x
=
sin
(
−
y
)
cos
x
+
cos
(
−
y
)
sin
x
=
(
2
)
,
(
3
)
−
sin
y
cos
x
+
cos
y
sin
x
=
sin
x
cos
y
−
cos
x
sin
y
{\displaystyle =\sin(-y)\cos x+\cos \left({\frac {\pi }{2}}-{\frac {\pi }{2}}-y\right)\sin x=\sin(-y)\cos x+\cos(-y)\sin x{\overset {(2),(3)}{=}}-\sin y\cos x+\cos y\sin x=\sin x\cos y-\cos x\sin y}
sin
(
x
+
y
)
=
sin
(
x
−
(
−
y
)
)
=
sin
x
cos
(
−
y
)
−
cos
x
sin
(
−
y
)
=
(
2
)
,
(
3
)
sin
x
cos
y
+
cos
x
sin
y
{\displaystyle \sin(x+y)=\sin(x-(-y))=\sin x\cos(-y)-\cos x\sin(-y){\overset {(2),(3)}{=}}\sin x\cos y+\cos x\sin y}
Las fórmulas para la tangente se pueden deducir de las cuatro fórmulas anteriores de igual forma que en la demostración particular anterior.
◻
{\displaystyle \quad \square }
De lo que se sigue para determinados ángulos suplementarios :
sen
(
π
±
x
)
=
∓
sen
(
x
)
{\displaystyle \operatorname {sen}(\pi \pm x)=\mp \operatorname {sen}(x)}
cos
(
π
±
x
)
=
−
cos
(
x
)
{\displaystyle \cos(\pi \pm x)=-\cos(x)}
tg
(
π
±
x
)
=
±
tg
(
x
)
{\displaystyle \operatorname {tg} (\pi \pm x)=\pm \operatorname {tg} (x)}
csc
(
π
±
x
)
=
∓
csc
(
x
)
{\displaystyle \csc(\pi \pm x)=\mp \csc(x)}
Para ángulos complementarios :
sen
(
π
2
−
x
)
=
cos
(
x
)
{\displaystyle \operatorname {sen} \left({\frac {\pi }{2}}-x\right)=\cos(x)}
cos
(
π
2
−
x
)
=
sen
(
x
)
{\displaystyle \cos \left({\frac {\pi }{2}}-x\right)=\operatorname {sen}(x)}
tg
(
π
2
−
x
)
=
cot
(
x
)
{\displaystyle \operatorname {tg} \left({\frac {\pi }{2}}-x\right)=\cot(x)}
csc
(
π
2
−
x
)
=
sec
(
x
)
{\displaystyle \csc \left({\frac {\pi }{2}}-x\right)=\sec(x)}
sec
(
π
2
−
x
)
=
csc
(
x
)
{\displaystyle \sec \left({\frac {\pi }{2}}-x\right)=\csc(x)}
cot
(
π
2
−
x
)
=
tg
(
x
)
{\displaystyle \cot \left({\frac {\pi }{2}}-x\right)=\operatorname {tg} (x)}
Para ángulos opuestos:
sen
(
−
x
)
=
−
sen
(
x
)
{\displaystyle \operatorname {sen} \left(-x\right)=-\operatorname {sen} \left(x\right)}
cos
(
−
x
)
=
cos
(
x
)
{\displaystyle \cos \left(-x\right)=\cos \left(x\right)}
tg
(
−
x
)
=
−
tg
(
x
)
{\displaystyle \operatorname {tg} \left(-x\right)=-\operatorname {tg} \left(x\right)}
csc
(
−
x
)
=
−
csc
(
x
)
{\displaystyle \csc \left(-x\right)=-\csc \left(x\right)}
sec
(
−
x
)
=
sec
(
x
)
{\displaystyle \sec \left(-x\right)=\sec \left(x\right)}
cot
(
−
x
)
=
−
cot
(
x
)
{\displaystyle \cot \left(-x\right)=-\cot \left(x\right)}
Otras relaciones:
2
sen
(
π
4
±
x
)
=
2
cos
(
π
4
∓
x
)
=
cos
(
x
)
±
sen
(
x
)
{\displaystyle {\sqrt {2}}\operatorname {sen} \left({\frac {\pi }{4}}\pm x\right)={\sqrt {2}}\cos \left({\frac {\pi }{4}}\mp x\right)=\cos \left(x\right)\pm \operatorname {sen} \left(x\right)}
editar
editar
Paso de producto a suma
editar
Puede probarse usando el teorema de la suma para desarrollar los segundos miembros.
sen
x
sen
y
=
cos
(
x
−
y
)
−
cos
(
x
+
y
)
2
{\displaystyle \operatorname {sen} x\operatorname {sen} y={\cos(x-y)-\cos(x+y) \over 2}}
cos
x
cos
y
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
2
{\displaystyle \cos x\cos y={\cos(x+y)+\cos(x-y) \over 2}}
sen
x
cos
y
=
sen
(
x
+
y
)
+
sen
(
x
−
y
)
2
{\displaystyle \operatorname {sen} x\cos y={\operatorname {sen}(x+y)+\operatorname {sen}(x-y) \over 2}}
cos
x
sen
y
=
sen
(
x
+
y
)
−
sen
(
x
−
y
)
2
{\displaystyle \cos x\operatorname {sen} y={\operatorname {sen}(x+y)-\operatorname {sen}(x-y) \over 2}}
Demostración
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
2
{\displaystyle \cos(x)\cos(y)={\cos(x+y)+\cos(x-y) \over 2}}
Sabemos por el teorema de la suma y la resta que:
cos
(
x
±
y
)
=
cos
(
x
)
cos
(
y
)
∓
sen
(
x
)
sen
(
y
)
{\displaystyle \cos(x\pm y)=\cos(x)\cos(y)\mp \operatorname {sen}(x)\operatorname {sen}(y)}
Si separamos la suma de la resta quedan entonces los dos posibles casos:
1):
cos
(
x
+
y
)
=
cos
(
x
)
cos
(
y
)
−
sen
(
x
)
sen
(
y
)
{\displaystyle \cos(x+y)=\cos(x)\cos(y)-\operatorname {sen}(x)\operatorname {sen}(y)}
cos
(
x
−
y
)
=
cos
(
x
)
cos
(
y
)
+
sen
(
x
)
sen
(
y
)
{\displaystyle \cos(x-y)=\cos(x)\cos(y)+\operatorname {sen}(x)\operatorname {sen}(y)}
Si tomamos la ecuación 1) y despejamos cos(x)cos(y) nos queda que:
3):
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
sen
(
x
)
sen
(
y
)
{\displaystyle \cos(x)\cos(y)=\cos(x+y)+\operatorname {sen}(x)\operatorname {sen}(y)}
Y si sumamos el miembro de la derecha de la ecuación 2) al miembro izquierdo de la ecuación 3), y para mantener la igualdad se suma el lado izquierdo de la ecuación 2) en el lado derecho de la ecuación 3) (al sumar la misma cantidad a ambos miembros de la ecuación la nueva ecuación sigue siendo cierta), quedaría:
cos
(
x
)
cos
(
y
)
+
sen
(
x
)
sen
(
y
)
+
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
sen
(
x
)
sen
(
y
)
+
cos
(
x
−
y
)
{\displaystyle \cos(x)\cos(y)+\operatorname {sen}(x)\operatorname {sen}(y)+\cos(x)\cos(y)=\cos(x+y)+\operatorname {sen}(x)\operatorname {sen}(y)+\cos(x-y)}
Simplificando el elemento sen(x)sen(y) y sumando cos(x)cos(y) quedaría:
2
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
{\displaystyle 2\cos(x)\cos(y)=\cos(x+y)+\cos(x-y)}
Y por último multiplicando ambos lados de la ecuación por ½ queda:
cos
(
x
)
cos
(
y
)
=
cos
(
x
+
y
)
+
cos
(
x
−
y
)
2
{\displaystyle \cos(x)\cos(y)={\cos(x+y)+\cos(x-y) \over 2}}
Nota 1: este procedimiento también se puede aplicar para demostrar el origen de las otras dos ecuaciones simplemente cambiando los valores.
Nota 2: Usando 3) y el resultado anterior se obtiene también:
sen
(
x
)
sen
(
y
)
=
cos
(
x
−
y
)
−
cos
(
x
+
y
)
2
{\displaystyle \operatorname {sen}(x)\operatorname {sen}(y)={\cos(x-y)-\cos(x+y) \over 2}}
Notar el cambio de signo.
Paso de suma a producto
editar
sen
a
+
sen
b
=
2
sen
(
a
+
b
2
)
cos
(
a
−
b
2
)
{\displaystyle \operatorname {sen} a+\operatorname {sen} b=\;\;\;2\operatorname {sen} \left({\frac {a+b}{2}}\right)\cos \left({\frac {a-b}{2}}\right)}
sen
a
−
sen
b
=
2
cos
(
a
+
b
2
)
sen
(
a
−
b
2
)
{\displaystyle \operatorname {sen} a-\operatorname {sen} b=\;\;\;2\cos \left({\frac {a+b}{2}}\right)\operatorname {sen} \left({\frac {a-b}{2}}\right)}
cos
a
+
cos
b
=
2
cos
(
a
+
b
2
)
cos
(
a
−
b
2
)
{\displaystyle \cos a+\cos b=\;\;\;2\cos \left({\frac {a+b}{2}}\right)\cos \left({\frac {a-b}{2}}\right)}
cos
a
−
cos
b
=
−
2
sen
(
a
+
b
2
)
sen
(
a
−
b
2
)
{\displaystyle \cos a-\cos b=-2\operatorname {sen} \left({\frac {a+b}{2}}\right)\operatorname {sen} \left({\frac {a-b}{2}}\right)}
tg
a
±
tg
b
=
sen
(
a
±
b
)
cos
a
cos
b
{\displaystyle \operatorname {tg} a\pm \operatorname {tg} b={\frac {\operatorname {sen}(a\pm b)}{\cos a\cos b}}}
Reemplazando x por (a + b ) / 2 e "y por (a – b ) / 2 en las identidades de producto a suma, se tiene:
Paso de diferencia de cuadrados a producto
editar
Paso de senos y cosenos a tangentes
editar
editar
editar
Las siguientes fórmulas de productos infinitos para funciones trigonométricas pueden ser útiles:
sen
x
=
x
∏
n
=
1
∞
(
1
−
x
2
π
2
n
2
)
cos
x
=
∏
n
=
1
∞
(
1
−
x
2
π
2
(
n
−
1
2
)
2
)
senh
x
=
x
∏
n
=
1
∞
(
1
+
x
2
π
2
n
2
)
cosh
x
=
∏
n
=
1
∞
(
1
+
x
2
π
2
(
n
−
1
2
)
2
)
{\displaystyle {\begin{aligned}\operatorname {sen} x&=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)\\\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)^{2}}}\right)\\\operatorname {senh} x&=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)\\\operatorname {cosh} x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)^{2}}}\right)\end{aligned}}}
e
+
i
x
=
cos
(
x
)
+
i
sen
(
x
)
{\displaystyle e^{+\mathrm {i} x}=\cos {\left(x\right)}+\mathrm {i} \operatorname {sen} {\left(x\right)}}
e
−
i
x
=
cos
(
x
)
−
i
sen
(
x
)
{\displaystyle e^{-\mathrm {i} x}=\cos {\left(x\right)}-\mathrm {i} \operatorname {sen} {\left(x\right)}}
Teorema del coseno
Dado un triángulo ABC, siendo α, β, γ, los ángulos, y a , b , c , los lados respectivamente opuestos a estos ángulos entonces:
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}
En todo triángulo se da la siguiente relación entre la longitud de sus lados a, b y c y el seno de sus respectivos ángulos opuestos A, B y C
a
sen
(
A
)
=
b
sen
(
B
)
=
c
sen
(
C
)
{\displaystyle {\frac {a}{\operatorname {sen}(A)}}={\frac {b}{\operatorname {sen}(B)}}={\frac {c}{\operatorname {sen}(C)}}}
El teorema del seno es usado con frecuencia para resolver problemas en los que se conoce un lado del triángulo y dos ángulos y se desea encontrar las medidas de los otros lados para posteriormente identificar los valores de las funciones trigonométricas.
La mayor parte de funciones trigonométricas admiten una formulación en términos de números complejos, algunos ejemplos:
Función
Función inversa
sen
θ
=
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \operatorname {sen} \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,}
arcsen
x
=
−
i
ln
(
i
x
+
1
−
x
2
)
{\displaystyle \operatorname {arcsen} x=-i\ln \left(ix+{\sqrt {1-x^{2}}}\right)\,}
cos
θ
=
e
i
θ
+
e
−
i
θ
2
{\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\,}
arccos
x
=
−
i
ln
(
x
+
x
2
−
1
)
{\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)\,}
tg
θ
=
e
i
θ
−
e
−
i
θ
i
(
e
i
θ
+
e
−
i
θ
)
{\displaystyle \operatorname {tg} \theta ={\frac {e^{i\theta }-e^{-i\theta }}{i(e^{i\theta }+e^{-i\theta })}}\,}
arctg
x
=
i
2
ln
(
i
+
x
i
−
x
)
{\displaystyle \operatorname {arctg} x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)\,}
csc
θ
=
2
i
e
i
θ
−
e
−
i
θ
{\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}\,}
arccsc
x
=
−
i
ln
(
i
x
+
1
−
1
x
2
)
{\displaystyle \operatorname {arccsc} x=-i\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,}
sec
θ
=
2
e
i
θ
+
e
−
i
θ
{\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}\,}
arcsec
x
=
−
i
ln
(
1
x
+
1
x
2
−
1
)
{\displaystyle \operatorname {arcsec} x=-i\ln \left({\tfrac {1}{x}}+{\sqrt {{\tfrac {1}{x^{2}}}-1}}\right)\,}
cot
θ
=
i
(
e
i
θ
+
e
−
i
θ
)
e
i
θ
−
e
−
i
θ
{\displaystyle \cot \theta ={\frac {i(e^{i\theta }+e^{-i\theta })}{e^{i\theta }-e^{-i\theta }}}\,}
arccot
x
=
i
2
ln
(
x
−
i
x
+
i
)
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)\,}
cis
θ
=
e
i
θ
{\displaystyle \operatorname {cis} \,\theta =e^{i\theta }\,}
arccis
x
=
ln
x
i
{\displaystyle \operatorname {arccis} \,x={\frac {\ln x}{i}}\,}
↑ V. Vodney y otros: Fórmulas matemáticas fundamentales , Editorial Euro-Omega, Madrid 1995, pág. 29
↑ Trigonometría (Segunda edición). Limusa(Noriega editores). ISBN 968-18-5617-1 Spiegel, M. & Abellanas, L.: "Fórmulas y tablas de matemática aplicada ", Ed. McGraw-Hill, 1988. ISBN 84-7615-197-7 .