Teoría de la homotopía

En matemáticas, la teoría de la homotopía es un estudio sistemático de situaciones en la cual las funciones pueden tener homotopías entre ellos. Se originó como un tema de la topología algebraica, pero, hoy en día, se estudia como una disciplina independiente. Además de la topología algebraica, la teoría también se ha utilizado en otras áreas de las matemáticas, como la geometría algebraica y la teoría de categorías.

Conceptos

Espacios y mapeos

En la teoría de la homotopía y la topología algebraica, la palabra "espacio" denota un espacio topológico . Para evitar patologías, rara vez se trabaja con espacios arbitrarios; en cambio, uno requiere espacios para cumplir con restricciones adicionales, como ser generado de forma compacta, o Hausdorff, o un complejo CW .

En la misma línea que arriba, un "mapeo" (también un aplicación) es una función continua, posiblemente con algunas restricciones adicionales.

Muchas veces, se trabaja con un espacio puntiagudo—un espacio con un "punto distinguido", se llama el punto base. Un mapeo puntiagudo es entonces un mapeo que conserva puntos base; es decir, envía el punto base del dominio al del codominio. Por el contrario, un mapeo libre es aquel que no necesita conservar los puntos base.

Homotopía

Artículo principal: Homotopía

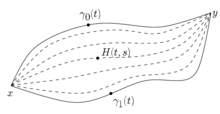
Denotemos $[0,1]$ el intervalo unitario. Una familia de mapeos indexados por $[0,1]$ , $h_{t}:X\to Y$ se llama homotopía de $h_{0}$ a $h_{1}$ si $h:[0,1]\times X\to Y,(t,x)\mapsto h_{t}(x)$ es un mapeo (debe ser una función continua ). Cuando $X$ , $Y$ son espacios puntiagudos, el $h_{t}$ tiene que conservar los puntos base. Se puede demostrar que una homotopía es una relación de equivalencia . Dado un espacio puntiagudo $X$ y un entero $n\geq 1$ , deja que $\pi _{n}(X)=[S^{n},X]_{*}$ sea las clases de homotopía de mapeos basados $S^{n}\to X$ de una n -esfera (puntiaguda) $S^{n}$ a $X$ . Como resulta, $\pi _{n}(X)$ son grupos. En particular, $\pi _{1}(X)$ se llama grupo fundamental de X.

Si se prefiere trabajar con un espacio (en general) en lugar de un espacio puntiagudo, existe la noción de un grupoide fundamental. Por definición, el grupoide fundamental de un espacio $X$ es la categoría donde los objetos son los puntos de $X$ y los morfismos son caminos.

Cofibracion y fibracion

Un mapeo $f:A\to X$ se llama un cofibración si, dado que (1) un mapeo $h_{0}:X\to Z$ y (2) una homotopía $g_{t}:A\to Z$ , existe una homotopía $h_{t}:X\to Z$ que se extiende $h_{0}$ y tal que $h_{t}\circ f=g_{t}$ . En cierto sentido, es parecido de diagrama definitorio de un módulo inyectivo en álgebra abstracta . El ejemplo más básico es un par CW $(X,A)$ , y dado que muchos individuos trabajan solo con complejos CW, la noción de cofibración a menudo está implícita.

Una fibración en el sentido del autor Serre es la noción dual de una cofibración: es decir, un mapa $p:X\to B$ es una fibración si se le da (1) un mapa $Z\to X$ y (2) una homotopía $g_{t}:Z\to B$ , existe una homotopía $h_{t}:Z\to X$ tal que $h_{0}$ es el dado y $p\circ h_{t}=g_{t}$ . Un ejemplo básico es un mapa de cobertura (de hecho, una fibración es una generalización de un mapa de cobertura). Si $E$ es un G -haz principal, es decir, un espacio con una acción de grupo libre y transitiva (topológica) de un grupo (topológico), entonces el mapa de proyección $p:E\to X$ es un ejemplo de una fibración.

Referencias

May, J. A Concise Course in Algebraic Topology
George William Whitehead (1978). Elements of homotopy theory. Graduate Texts in Mathematics 61 (3rd edición). New York-Berlin: Springer-Verlag. pp. xxi+744. ISBN 978-0-387-90336-1. MR 0516508. Consultado el 6 de septiembre de 2011.
Ronald Brown, Topology and groupoids (2006) Booksurge LLC ISBN 1-4196-2722-8.

Otras lecturas

https://ncatlab.org/nlab/show/homotopy+theory