Se ha propuesto fusionar este artículo o sección con «teorema del valor medio », pero otros wikipedistas no han alcanzado consenso sobre este asunto. Para más información, véase la discusión . Lee la página de discusión de ambos artículos y aporta tus razones antes de proceder, respetando las normas de civismo en páginas de discusión .Uso de esta plantilla: {{sust:Fusionar|Nombre de hasta otros veinte artículos para fusionar separados por "|"}}
En análisis matemático , y más concretamente en cálculo diferencial , el teorema del valor medio de Cauchy es una generalización del teorema del valor medio (de Lagrange ). A partir de este puede demostrarse la regla de L'Hôpital , fuerte ayuda para el cálculo de límites con indeterminaciones
0
0
{\displaystyle \textstyle {\frac {0}{0}}}
∞
∞
{\displaystyle \textstyle {\frac {\infty }{\infty }}}
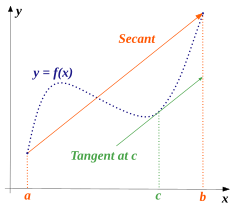
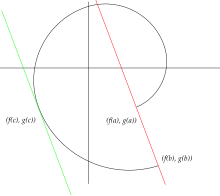
Interpretación geométrica: para cualquier función continua en
[
a
,
b
]
{\displaystyle [a,b]}
(
a
,
b
)
{\displaystyle (a,b)}
c
{\displaystyle c}
(
a
,
b
)
{\displaystyle (a,b)}
[
a
,
b
]
{\displaystyle [a,b]}
c
{\displaystyle c}
Existe un punto del arco fijado donde la tangente es paralela a la cuerda.
El teorema, aparecido en su Cours d’Analyse (1821),[ 1]
Sean
f
{\displaystyle f}
g
{\displaystyle g}
[
a
,
b
]
{\displaystyle [a,b]}
(
a
,
b
)
{\displaystyle (a,b)}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
(
f
(
b
)
−
f
(
a
)
)
g
′
(
c
)
=
(
g
(
b
)
−
g
(
a
)
)
f
′
(
c
)
.
{\displaystyle (f(b)-f(a))g\,'(c)=(g(b)-g(a))f\,'(c).\,}
En el caso de que g (a ) ≠ g (b )g ′(c ) ≠ 0
f
′
(
c
)
g
′
(
c
)
=
f
(
b
)
−
f
(
a
)
g
(
b
)
−
g
(
a
)
⋅
{\displaystyle {\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}\cdot }
Nótese el caso particular en el cual g(x)=x , donde entonces la expresión se reduce al teorema del valor medio de Lagrange .
Sea G(x ) una función definida como:
G
(
x
)
=
[
g
(
b
)
−
g
(
a
)
]
⋅
[
f
(
x
)
−
f
(
a
)
]
−
[
f
(
b
)
−
f
(
a
)
]
⋅
[
g
(
x
)
−
g
(
a
)
]
{\displaystyle G(x)=[g(b)-g(a)]\cdot [f(x)-f(a)]-[f(b)-f(a)]\cdot [g(x)-g(a)]\,\!}
donde f(x) y g(x) son funciones continuas en [a ,b ], derivables en (a ,b ). Se puede observar por simple inspección que G(a)=0 y G(b)=0 .
G
′
(
x
)
=
[
g
(
b
)
−
g
(
a
)
]
⋅
f
′
(
x
)
−
[
f
(
b
)
−
f
(
a
)
]
⋅
g
′
(
x
)
{\displaystyle G'(x)=[g(b)-g(a)]\cdot f'(x)-[f(b)-f(a)]\cdot g'(x)}
y sabiendo que G'(c) es 0
0
=
[
g
(
b
)
−
g
(
a
)
]
⋅
f
′
(
c
)
−
[
f
(
b
)
−
f
(
a
)
]
⋅
g
′
(
c
)
{\displaystyle 0=[g(b)-g(a)]\cdot f'(c)-[f(b)-f(a)]\cdot g'(c)}
de donde se deduce que
[
f
(
b
)
−
f
(
a
)
]
⋅
g
′
(
c
)
=
[
g
(
b
)
−
g
(
a
)
]
⋅
f
′
(
c
)
{\displaystyle [f(b)-f(a)]\cdot g'(c)=[g(b)-g(a)]\cdot f'(c)}
Si g(b)-g(a) y g'(c) son distintos de 0, la expresión anterior puede ser escrita como:
f
(
b
)
−
f
(
a
)
g
(
b
)
−
g
(
a
)
=
f
′
(
c
)
g
′
(
c
)
{\displaystyle {\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}}
Q.E.D.
El teorema de Cauchy es usado para la demostración de otros teoremas. Nos permite, entre otros, demostrar la regla de L'Hôpital :
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
f
′
(
x
)
g
′
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}}
muy usada en análisis matemático , para el cálculo de límites de la forma de
0
0
{\displaystyle \textstyle {\frac {0}{0}}}
∞
∞
{\displaystyle \textstyle {\frac {\infty }{\infty }}}
↑ Nicolas Bourbaki, Éléments d'histoire des mathématiques , p. 193.
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle G(x)=[g(b)-g(a)]\cdot [f(x)-f(a)]-[f(b)-f(a)]\cdot [g(x)-g(a)]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb5a04a20ed96034a0cc2dea0ee9a979e6d7b9d)
![{\displaystyle G'(x)=[g(b)-g(a)]\cdot f'(x)-[f(b)-f(a)]\cdot g'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/056e04c69b2d92f978dbcd54c6e424fac8e44a68)
![{\displaystyle 0=[g(b)-g(a)]\cdot f'(c)-[f(b)-f(a)]\cdot g'(c)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b5172e5e43e74aa7355df69861e9a5a42ef92a0)
![{\displaystyle [f(b)-f(a)]\cdot g'(c)=[g(b)-g(a)]\cdot f'(c)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a32774f1a2776b4129e6acf34665d66b9f5ad89)
Datos: Q3325219